2. Идеальный бозе-газ, состоящий из частиц, масса покоя которых не равна нулю

2.1. Применение распределений Бозе и Ферми к идеальным газам, состоящим из частиц, масса покоя которых не равна нулю

Распределение Бозе для частиц, имеющих нулевой или целый спин, и распределение

Ферми для частиц с полуцелым спином имеют следующий вид [8]

. (2.1) Здесь - среднее число частиц, 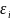- энергия частицы в – ом квантовом состоянии , - постоянная Больцмана, , - спин частицы, - её химический потенциал, знак плюс и минус соответствуют соответственно распределениям Ферми и Бозе. Очевидно, что полное число частиц в идеальных бозе- и ферми-газах равно [8]

(2.2) Внутренняя энергия идеального бозе- и ферми- газов, состоящих из частиц,

(2.3) Наконец, большой термодинамический потенциал Гиббса

(2.4)

2.2 Нахождение элементарного числа квантовых состояний частицы

Величину

Г = (2.5)

называют элементом фазового объёма. Авторы работы [8] представляют элемент фазового объёма в следующем виде

Г = (2.6)

где . Следует отметить, что в (2.5) Г представляет собой прямоугольное шестимерное фазовое пространство, в котором введены прямоугольные координаты как в пространстве положений частицы { , так и в пространстве её импульсов . Так как подинтегральные выражения в формулах (2.2) –(2.4) не зависят от координат положения частицы, то мы можем проинтегрировать (2.6) по этим координатам. Получим

Г´= (2.7)

где - объём куба с длиной ребра . Здесь предполагается, что Авторы [8], [9] в импульсном пространстве переходят от прямоугольной системы координат к сферической системе координат, оставляя в пространстве положений частиц прямоугольную систему координат