Лабораторная работа №2

ДИНАМИКА ЦИФРОВЫХ РЕКУРСИВНЫХ СИСТЕМ ПЕРВОГО ПОРЯДКА ПРИ ПОСТОЯННОМ ВНЕШНЕМ ВОЗДЕЙСТВИИ

Цель работы: изучение переходных и стационарных режимов, возникающих в линейных и нелинейных цифровых рекурсивных системах первого порядка при постоянном внешнем воздействии.

Теория

Цифровые системы (цепи) первого порядка широко используются в современных системах передачи информации. На их базе реализуются фильтры нижних (ФНЧ) и верхних (ФВЧ) частот. В качестве носителя информации часто используется прямоугольный импульс. Поэтому практически важными являются вопросы исследования колебательных режимов при постоянном внешнем воздействии. Полагаем, что эффекты квантования отсутствуют, цепь устойчива, т.е. параметр (коэффициент) ее b1 <1.

1. Линейная система

Структурная схема линейной рекурсивной цифровой системы первого порядка представлена на рис.1.

21

Колебания в ней при постоянном внешнем воздействии A описываются линейным разностным уравнением

Поскольку b1 <1, в установившемся режиме получим

Введем последовательность y2(n)=y1(n+1). Разностному уравнению (1) соответствует функция последования

y2=b1y1+A.

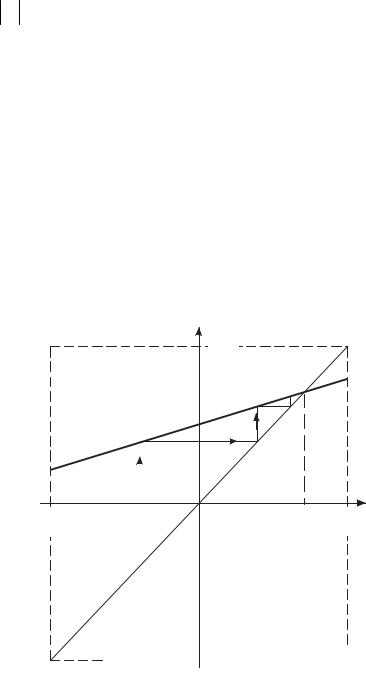
Выражение для Y1 может быть получено и как формула для абсциссы точки пересечения графиков функции последования и биссектрисы

первого и третьего координатных углов (рис. 2). y2

1

y1 y= 2

-1

Рис. 2

22

Рассмотрим процессы в системах с двумя видами характеристики сумматора: с насыщением и пилообразной. Полагаем, что в фильтре используются арифметика с фиксированной запятой и числа, выровненные слева.

Взависимости от значений b1 и А в системе возможен линейный

инелинейный режим.

Линейный режим

Пусть b1>0 (цепь является ФНЧ). Пример диаграммы Ламерея для А>0 показан на рис. 2. Согласно (3) условием линейного режима является

1-Ab1 ≤1,

откуда следует

Эта область показана заштрихованной на рис. 4.

Пусть b1<0 (цепь является ФВЧ). Пример диаграммы Ламерея при А>0 показан на рис. 5.

24

-1

Рис. 5

В линейном режиме модуль абсциссы точки пересечения функции последования и биссектрисы второго и четвертого координатных углов меньше или равен 1. Отсюда следует

−A ≤1, 1+b1

т.е.

И эта область показана заштрихованной на рис. 4.

При выборе b1 и А за пределами показанной на рис.4 области в колебательной системе возникает нелинейный режим. Характер поведения системы в этом случае зависит от вида характеристики сумматора.

Характеристика сумматора с насыщением

Характеристика сумматора с насыщением выражается функцией

25

График ее показан на рис. 6.

Характер поведения системы в этом случае зависит от знака b1. Пусть b1>0. Пример диаграммы и лестницы Ламерея при А>0

показан на рис. 7.

После включения постоянного воздействия в цепи существует линейный режим до достижения y2 =1. Длительность этого режима находится из (2) и при y1(0)=0 выражается функцией

26

где [•] - целая часть числа, величина Y1 находится из (3). Далее имеет

место режим с насыщением, а полная длительность переходного процесса на 2 единицы больше, чем величина N1.

Пусть b1<0. Пример диаграммы и лестницы Ламерея при А>0 показан на рис. 8. При этом отображение имеет единственную неподвижную точку с координатой Y1, определяемой из (3). Здесь начальное состояние y1(0) соответствует режиму с насыщением, а при

насыщением и линейный (при n ≥1).

-1

Рис. 8

27

Рис. 10

Исследуем устойчивость цикла периода T = 2. С помощью обобщенной теоремы Кенигса определим устойчивость двукратной неподвижной (инвариантной) точки Y1 (0). В данном случае имеем

Следовательно, точка Y1 (0), а вместе с ней и точка Y1 (1) (а вместе с ними и цикл периода T = 2) устойчивые.

29

Выражения (6) и (7) позволяют определить область параметров (b1, A), соответствующую периоду T = 2. При A > 0 нижняя граница

этой области находится из условия

а верхняя граница – из условия

Из выражений (6) и (8) получим

A ≥ 1+b12 , 1+b1

а из (7) и (9) имеем выражение для верхней границы

A < 1+2b1 −b12 . 1+b1

На рис. 11 заштрихованной показана область, соответствующая колебаниям с периодом T = 2. Вследствие специфики характеристики сумматора верхняя граница этой области задается прямой A =1.

30

Рассмотрим колебательный процесс с периодом T = 3. Диаграмма Ламерея при b1 = 0,6, A = 0,7 приведена на рис. 12.

Рис. 12

Пусть система стартует из точки y1 (0)=Y1 (0). Тогда y1 (1)=Y1 (1)= b1Y1 (0)+ A , y1 (2)=Y1 (2)= b1 y1 (1)+ A . Согласно правилу

31

По аналогии со случаем T = 2 нетрудно определить устойчивость трехкратной неподвижной (инвариантной) точки Y1 (0).

В данном случае имеем

Следовательно, согласно обобщенной теореме Кенигса, точка Y1 (0), а вместе с ней и точка Y1 (1) и Y1 (2) (а вместе с ними и цикл периода

T = 3) устойчивые.

С помощью выражений (8) и (9) определим область параметров (b1, A), соответствующую T = 3. Из (8) и (10) для нижней границы

получим

из (9) и (11) имеем выражение для верхней границы этой области

A < 1+ 2b12 −b13 . 1+b12 +b1

На рис. 13 заштрихованной показана область, соответствующая колебаниям с периодом T = 3.

32

Распространим установленные закономерности на случай произвольного периода T . При этом должно выполняться равенство

Y1 (T )=Y1 (0),

T −2

где Y1 (T )= b1Y1 (T −1)+ A −2 ,Y1 (T −1)= b1T −1Y1 (0)+ A∑b1i .

33

Пусть b1 < 0 . Пример диаграммы Ламерея при A > 0 показан на

рис. 15. В отличие от системы, имеющей сумматор с насыщением (см. рис. 8), в данном случае графики функции последования и

Заметим, что режиму ФВЧ соответствует только точка B . Приведенные на рис. 15 лестницы Ламерея показывают, что координата неподвижной точки зависит от начального условия y1 (0).

35