Лабораторная работа №6

ДИНАМИКА ЦИФРОВОЙ РЕКУРСИВНОЙ СИСТЕМЫ ПЕРВОГО ПОРЯДКА С УЧЕТОМ ЭФФЕКТОВ КВАНТОВАНИЯ

Цель работы: изучение свободных колебаний и колебаний при постоянном входном воздействии в цифровой рекурсивной системе первого порядка с квантованием (путем округления) результатов сложения. В системе используется целочисленная арифметика с прямым кодом.

Теория

1. Исходные положения

Цифровые системы (цепи) первого порядка широко распространены в системах передачи информации. Они используются самостоятельно в качестве фильтров нижних (ФНЧ) и верхних (ФВЧ) частот, а также в совокупности с цепями второго порядка при каскадной (или последовательной) и параллельной формах реализации цифровых фильтров высокого порядка.

Специфика цифровых систем по сравнению с аналоговыми обусловлена конечной точностью представления чисел из-за ограниченного количества используемых двоичных разрядов. Вследствие этого цифровая колебательная система в общем случае является существенно нелинейной. В ней возникают специфические ошибки, называемые эффектами квантования.

При достаточно большом количестве разрядов эти эффекты незначительны, и для анализа их влияния используется линейная статистическая модель системы. Однако такая модель неприемлема при воздействии постоянного или синусоидального сигнала, дискретизированного с частотой, кратной частоте синусоиды, а также при малом количестве разрядов.

Последнее обстоятельство характерно для цифровых фильтров, используемых при обработке радиосигналов в реальном времени. При этом числа представляются, как правило, в форме с фиксированной запятой.

Рассмотрим процессы в цифровой рекурсивной системе первого порядка с параметром (коэффициентом) b1 , выбранным в пределах

105

устойчивости линейной системы, т.е. b1 <1. Полагаем, что

используется арифметика с фиксированной запятой, точно задается коэффициент b1 и выполняется операция умножения, а квантуются

путем округления результаты сложения чисел, представленных в прямом коде. Результаты суммирования представляются в виде последовательности целых чисел. Сумматор без учета квантования имеет линейную характеристику.

Рис. 1

Количество уровней квантования L при таком выборе кодирования чисел связано с количеством разрядов M в представлении чисел следующей зависимостью:

L = 2M +1 −1.

При использовании целочисленной арифметики шаг квантования равен единице, а характеристика квантователя (сумматора) чисел, представленных в прямом или обратном кодах с округлением, выражается функцией

f (ϕ)= ϕ +12sign (ϕ) ,

106

Колебания в рекурсивной системе первого порядка с квантованием результатов сложения описываются разностным уравнением

y1 (n +1)= f (b1 y1 (n)+ x(n +1)).

Участки характеристики квантователя, соответствующие значениямϕ +12sign (ϕ) , обозначим 0, ±1, ±2, …, ±N . Имеем в виду, что

107

вследствие квантования в системе первого порядка возможны L состояний.

В общем случае в зависимости от начального состояния в нелинейной системе возможны различные установившиеся движения. Поскольку все L возможных начальных состояний равновероятны и независимы, введем понятие вероятности P установившегося движения B в виде

P (B)= mL ,

где m – количество начальных состояний, соответствующих этому движению.

Плоскость состояний разбиваем на области соответственно участкам характеристики сумматора (квантователя). Обозначим эти области, как и соответствующие участки. При этом граница областей

2. Свободные колебания

Свободные колебания описываются нелинейным разностным уравнением

108

y2 (n +1) − f (b1 y1 (n))= 0,

а функция последования имеет вид y2 = f (b1 y1 ). При всех значениях коэффициента b1 одной из точек пересечения графика функции последования и биссектрисы y2 = y1 является начало координат, что

соответствует простой неподвижной (инвариантной) точке отображения.

абсциссами Y1 = ±1, если граница областей 0, 1 проходит через точку y1 =1, а граница областей −1, 0 – через точку y1 = −1 соответственно. При этом согласно (1) выполняются условия y1 = ±1(2b1 )= ±1, т.е.

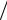b1 =12.

Следовательно, система имеет единственное состояние равновесия – состояние покоя – при b1 (0; 12). При b1 ≥12 число

неподвижных точек увеличивается.

В качестве примера на рис. 3 обозначены области плоскости состояний и построена диаграмма Ламерея при b1 = 45.

Определяемые из (1) уравнения границ областей сведены в табл. 1.

Таблица 1

Уравнения границ областей при b1 = 45, x = 0

Y1 {0; ±1; ±2}, которым соответствуют колебания с периодом T =1 и

мгновенными значениями y1 =Y1 . При старте из точки y1 > 2 и y1 < −2 в системе устанавливаются колебания соответственно T =1(±2). Значит, вероятности возможных колебаний равны P (0)= P (±1)=1L ,

P (±2)= (N −1)L .

109

Y1 −1 2 ≤ b1Y1 <Y1 +1 2 ∩Y1 −1 2 ≤ b1 (Y1 +1)<Y1 +12,

110

T =1(±Y1 ), где Y1 [0; N ], с вероятностью P =1L . При этом согласно

(1) выполняется условие

y1 = (12 + N −1)b1 = N , т.е.b1 =(N −12)N .

Значит, такие колебания возможны в интервале значений коэффициента

координат. При уменьшении коэффициента b1 от нуля в данном

отображении появляются и неподвижные (инвариантные) точки кратности 2: Y1 = ±1, когда графики функции последования и

биссектрисы y2 = −y1 пересекаются в точках с абсциссой Y1 = ±1. При этом граница областей −1, 0 проходит через точку y1 =1. Согласно

(1) это означает выполнение условия

y1 = −1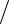(2b1 )=1, т.е. b1 = −12.

Следовательно, в интервале значений b1 (−12; 0) система

имеет единственное состояние равновесия – состояние покоя. При дальнейшем уменьшении коэффициента b1 от b1 = −12 число

неподвижных точек кратности 2 увеличивается.

В качестве примера на рис. 4 обозначены области плоскости состояний и построена диаграмма Ламерея при b1 = −45 . Области, на

которые разбивается плоскость состояний, располагаются зеркально относительно оси ординат по сравнению с изображенными на рис. 3. Данное отображение имеет простую неподвижную точку в начале

мгновенными значениями y1 = ±Y1 .

При старте из точек y1 > 2 и y1 < −2 в системе устанавливаются колебания T = 2(2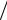−2). Таким образом, вероятности возможных колебаний равны: P (0)=1L , P (1−1)= 2L , P (2−2)= (L −3)L .

111

−(Y1 +12)< b1Y1 ≤ −(Y1 −12)∩−(Y1 +12)< b1 (Y1 +1)≤ −(Y1 −12),

откуда следует

112