Лабораторная работа № 1

ДИНАМИКА АВТОНОМНЫХ ЦИФРОВЫХ РЕКУРСИВНЫХ СИСТЕМ ПЕРВОГО ПОРЯДКА

Цель работы: изучение свободных колебаний, типов и характеров движений, возникающих в линейных и нелинейных цифровых рекурсивных системах первого порядка, построение бифуркационных диаграмм исследуемых систем.

Теория

1. Свободные колебания в линейной рекурсивной системе первого порядка

Цифровые системы (цепи) первого порядка широко распространены в системах передачи информации. Они используются самостоятельно в качестве фильтров нижних и верхних частот, а также в совокупности со звеньями второго порядка при каскадной (или последовательной) и параллельной схемах реализации цифровых фильтров высокого порядка.

Структурная схема рекурсивной системы изображена на рис 1. Здесь x(n+1) – входное воздействие, y(n+1) – реакция системы, z-1 – элемент задержки, b1 – умножитель с коэффициентом b1, блок f(ϕ)

определяет вид характеристики сумматора. Тип этой характеристики (линейный или нелинейный) определяет тип динамической системы.

z-1

b1

y1(n)

Рис. 1

5

Изучение свободных колебаний динамической системы играет большую роль, поскольку оно дает сведения об устойчивости системы, позволяет установить влияние параметров системы на ее основные динамические характеристики. Известно, что свободные колебания динамической системы описываются однородным уравнением. Линейной системе соответствует характеристика сумматора f(ϕ)=ϕ. Однородное разностное уравнение линейной рекурсивной системы при ненулевом начальном условии (y1(0)≠0)

имеет вид

Введем функцию y2(n) = y1(n+1), тогда уравнение примет вид

Исследование процессов в системах первого порядка удобно проводить методом одномерных точечных отображений. В случае системы первого порядка точечное отображение задается функцией последования y2=b1y1. Точки y1(n) и y1(n+1) = y2(n) называются

соответственно начальной и последующей или точкой-оригиналом и точкой-образом. Точка y1(n) называется n-й итерацией начального

значения y(0).

Точка y1* , являющаяся корнем уравнения b1y1 - y1 = 0, т.е.

отображающаяся сама в себя ( y1* = b1 y1* ), называется простой неподвижной

точкой отображения. На диаграмме Ламерея простая неподвижная точка

является точкой пересечения графика функции последования с биссектрисой y2 = y1. Как видно из рис. 2, неподвижная точка может

являться пределом последовательности (2). Опираясь на следствия теорем о существовании и единственности кратных циклов одномерного

точечного отображения, можно утверждать, что отображение (2) имеет простую неподвижную точку в начале координат (см. рис. 2) при b1 > 0 и

не имеет кратных неподвижных точек при b1 > -1. Кроме того, при | b1 | < 1 имеется единственная устойчивая простая неподвижная точка – начало координат (см. рис. 2 и 3).

6

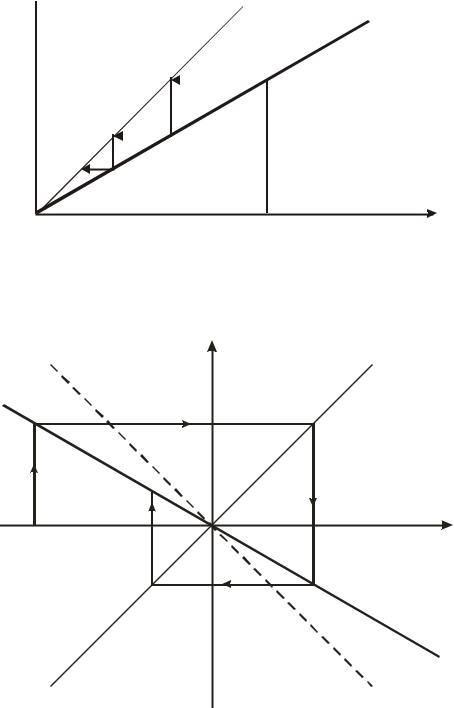
При b1< 0 отображение не имеет неподвижных точек кратности выше второй. При b1= -1 существует нейтрально устойчивый цикл периода T = 2 (рис. 4). При b1= 1 существуют нейтрально устойчивые состояния равновесия (рис. 5).

7

Рис. 4

y2

y1(0) y1(0)

Рис. 5

Если | b1 | > 1, то отображение имеет единственную неподвижную

точку в начале координат. Согласно теореме Кенигса она неустойчива

(рис. 6 и 7).

8