Задания

19. Для представленных ниже конфигураций найти распределение магнитостатического поля, построить эквипотенциальные кривые и графики изменения напряженности поля вдоль нескольких линий.

При неуказанных размерах геометрию области задавать приближенно, сохраняя конфигурацию и масштаб рисунка. В случае затруднений обращаться к преподавателю.

1) Цилиндр с проницаемостью 1 в вакууме 1=0.01; 0.333; 3; 10; 100.	4) Пластина
2) Бесконечный полый цилиндр r2 : r1 = 3 : 2; 2 : 1; 3 : 1. 1 = 5; 10; 100.	5) Система плотно прилегающих пластин с различными проницаемостями 1 = 5; 2 = 10; 3 = 20.
3) Полый цилиндр с дном	6) Полый шар r3:r2:r1=5:4:3; 3:2:1; 5:3:1. 1 = 3, 2 = 5; 1 = 3, 2 = 10.
7) 1 = 5; 50; 100.	8) 1) 1 = 3; 2 > 1 2) 1 = 1; 2 = 10; 3 = 20

20. Найти стационарное распределение температуры в области, представленной на рис. 15, если подобласти ₁ и ₂ заполняют среды с коэффициентами теплопроводности k₁  k₀ и k₂  k₀ (k₀ – коэффициент теплопроводности в остальной части области). На внешней границе области использовать подходящие условия температурного режима.

21. Решить задачу о распределении магнитного поля для областей, представленных в задании 19, используя формулировку на основе векторного потенциала:

.

22. Найти распределение магнитостатического поля в области, представленной на рис. 15, если через проводники ₁ и ₂ с магнитными проницаемостями ₁ и ₂ протекают токи с постоянной плотностью j₁ и j₂ соответственно.

Решить ту же задачу, если j₂ = 0, j₁  0, а также для случая, когда оба проводника помещены во внешнее однородное магнитное поле Н_е.

Указание. Для решения использовать следующую формулировку:

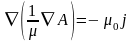внутри проводника,

вне проводника.

Лабораторная работа № 6 Решение уравнения Лапласа в области с разрезами

В задачах расчета магнитостатического поля вблизи массивных сверхпроводников через скалярный магнитный потенциал требуется решить уравнение Лапласа

с учетом однородного условия Неймана на границе сверхпроводника, с граничными условиями 1-го и 2-го рода на остальных границах и дополнительным условием скачка на некоторой поверхности (в двумерном варианте – линии) разреза . Условие скачка означает, что каждой точке разреза потенциалу приписывается два значения (по одну и по другую сторону разреза), отличающихся между собой на одно и то же число – силу тока I. В результате получается, что потенциал при переходе через  терпит скачок, равный I. Точная математическая формулировка такой задачи предполагает два варианта задания условий на :

1) известен текущий в сверхпроводнике ток, тем самым задается вполне определенный скачок потенциала

;

2) известен фиксированный поток ₀ через поверхность (линию) разреза, т.е. ставится интегральное условие

,

при одновременном выполнении условия скачка (точное значение этого скачка заранее неизвестно; оно определится после решения задачи).

Разрез проводится так, чтобы из двусвязной область превратилась в односвязную. В двумерных задачах он, как правило, соединяет сверхпроводник и внешнюю границу расчетной области. В осесимметричных задачах наиболее естественным представляется проведение линии разреза от сверхпроводника к оси z (в этом случае разрез будет закрывать отверстие сверхпроводящего кольца).

Приведенная постановка задачи обобщается на любое число токонесущих сверхпроводников, при этом к каждому из них проводится свой разрез с соответствующим значением либо I_i, либо _0i.

Замечание. При решении рассматриваемых здесь задач необходимо помнить, что при наличии граничных условий только Неймана (а это наиболее частый случай) все ограничения на потенциал формулируются относительно разности его значений (проверьте!). Это означает, что скалярный магнитный потенциал определяется с точностью до константы. Метод конечных элементов не приемлет такой неоднозначности, поэтому, чтобы ее исключить, необходимо задать вполне конкретное значение потенциала (например, ноль) в каком-либо узле P конечно-элементной сетки.

Пример 9. Найти распределение магнитного поля, создаваемого бесконечным сверхпроводниковым проводом круглого сечения с током I=1 A внутри сверхпроводниковой полости (см. рис. П20). Положить R₂/R₁=3.

П орядок решения:

1) Запустить pre2d.exe. Ввести новый номер задачи.

2) Ввод четвертой части геометрии области:

– ввести узлы с координатами (0,0), (1,0), (0,1), (3,0), (0,3);

– ввести линию как дугу окружности, соединяя узлы 2 и 3, относительно центра 1; аналогично ввести линию, соединяющую узлы 4 и 5 по окружности с тем же центром;

– ввести четырехугольную зону по линиям 1 и 2.

3) Получить всю область, дважды применяя операцию зер­кального отображения: первый раз отобразить зону 1 относи­тельно оси 1–3, а второй раз – зоны 1 и 2 относительно оси 7–4.

4) Ввести разрез и скачок потенциала на нем. Линией раз­реза может быть любая линия, «разрезающая» область в ради­альном направлении, например, линия 4.

«Файл»  «Граничные условия»  «Разрез» [4,1,9] <Enter>

5) Произвести разбиение зон, определяя числа деления в любой зоне как 45 и 30.

6) Проверить, что задано действительно уравнение Лапласа.

7) Задать условие u=0 в каком-либо узле сети, не лежащем на разрезе (таким узлом, например, является узел 2000):

«Файл»  «Граничные условия»  «Условие в узле сети» [2000,0].

8) Выйти из программы pre2d и, следуя стандартной схеме, запустить последовательно программы appl_fem, difeqt, post2d.

9) Как обычно, отобразив в программе post2d картину поля, вывести затем значения напряженности поля в радиальном направлении, определить энергию поля. Сравнить результаты с аналитическими формулами:

; .

1 0) Вычислить силу, действующую на провод. Для этого следует предварительно пометить линии, лежащие на границе провода (F7), а затем войти в меню «Вычислить» и выбрать «Найти силу».

Модификации. На основе введенной геометрии путем несложных изменений легко получить решения следующих задач.

а) Смещенный круглый провод внутри цилиндрической полости (рис. П21).

Примерные шаги: загрузив предыдущую задачу в режиме «Данные для автоматического разбиения», выбрать операцию «Сдвиг»«Линии»[список линий:]<Enter>[вектор сдвига: 0.8,0] <Enter>, разбить на конечные элементы по типу предыдущей задачи <Ctrl+F8> и далее – по стандартной схеме (внимание: условие в узле сети не сохраняется, его необходимо снова вводить!).

З агрузка задачи в режиме «Только геометрия» предполагает после выполнения операции сдвига или параллельного переноса линий, составляющих границу провода, проведения нового разбиения зон (что при большом смещении может оказаться оправданным).

б) Провод в виде кольца круглого сечения (тор) внутри тороидальной полости (рис. П22).

Предположим, что радиус тора равен R (очевидно, R>R₂). Если центр сечения O рассмотренной в примере задачи совпадает с началом координат, то, смещая всю область вверх на R единиц, получим требуемую геометрию задачи. Под координатами (x, y) при этом соответственно понимаем (z, r) цилиндрической системы. Задача теперь формулируется как осесимметричная: вращая область вокруг оси z, получим нужные пространственные объекты.

Пусть R=4,5. Примерные действия: загрузить одну из рассмотренных здесь плоских задач (смещенный или несмещенный провод внутри полости) в режиме «Данные для автоматического разбиения»; выбрать операцию «Сдвиг» «Зоны» [список зон; перечислить все зоны:1,2,3,4] <Enter> [вектор сдвига: 4.5,0] <Enter>; разбить на конечные элементы по типу предыдущей задачи <Ctrl+F8>. Далее – по стандартной схеме (внимание: условие в узле сети не сохраняется, его необходимо снова вводить!).