Упражнения

1. Провести дискретизацию задачи (3.51–3.53) с учетом граничных условий Неймана методом Ритца. Показать, что условие (3.52) является естественным.

2. Нужно ли в этой формулировке задавать фиксированное значение в одном узле конечноэлементной сетки?

3. Получить дискретные уравнения в цилиндрической системе координат.

Г. Проникновение магнитного поля в сверхпроводниковый экран

Для описания проникновения магнитного поля в сверхпроводник воспользуемся моделью Ф. и Г. Лондонов, которая справедлива в узкой области температур около температуры сверхпроводящего перехода, когда магнитное поле у поверхности сверхпроводника изменяется достаточно медленно.

Для чистого металла энергию, обусловленную наличием магнитного поля, можно представить в виде

Е = Е_k + Е_m ,

где Е_k – кинетическая энергия, связанная с незатухающими токами; Е_m – энергия, связанная с магнитным полем . Если обозначить е – заряд электрона; n_s – число сверхпроводящих электронов в единице объема; т – эффективная масса электрона; – скорость дрейфа электронов в точке , то кинетическая энергия определяется следующим образом:

.

Это выражение остается справедливым при условии, что скорость – медленно меняющаяся функция координат. Е_магн , как обычно, определяется соотношением

.

Учитывая, что плотностью тока связана с выражением

,

а поле связано с уравнениями , , имеем

, (3.54)

где величина _L имеет размерность длины и определяется так:

.

Будем теперь минимизировать энергию (3.54) относительно распределения поля . При изменении величины поля на величину энергия Е меняется на Е:

.

Следовательно, конфигурация поля внутри образца, приво­дящая к минимуму энергии, должна удовлетворять уравнению

. (3.55)

Совместно с уравнениями Максвелла

, (3.56)

, (3.57)

оно позволяет находить распределение полей и токов.

Рис. 3.13.

Применим теперь уравнение Лондонов (3.55) к задаче о проникновении магнитного поля в сверхпроводник. Выберем простейшую геометрию: поверхность образца совпадает с плоскостью xy, область z < 0 является пустой. Тогда поле и ток зависят лишь от z. Пусть поле тангенциально и направлено вдоль оси x. В этом случае уравнение (3.57) удовлетворяется автоматически, а из уравнения (3.56) следует, что ток направлен вдоль оси y:

.

Уравнение (3.55) дает

.

Решение, конечное внутри сверхпроводника, является экспоненциально убывающим:

.

Таким образом, на глубине проникновения _L поле убывает в е раз, а на расстояниях, в несколько раз превышающих _L, поле становится пренебрежимо малым.

Упражнения

1. Показать, что если поле в указанной задаче параллельно оси z, то решение уравнения (3.55) есть = 0, т.е. поле не может быть нормально к поверхности образца.

2. Провести дискретизацию методом Ритца уравнения (3.55), минимизируя функционал (3.54). Дать конечно-элементную формулировку задачи.

Д. Электромагнитные экраны

Данный тип экранов характеризуется наличием переменного (электро)магнитного поля, действующего на проводник. Требуется определить распределение поля внутри проводника, на которого действует внешнее поле H₀. Условия квазистационарного поля приводят к тому, что воздействие внешнего поля полностью определяется его значениями на границе проводника. Пусть геометрия области задачи имеет трансляционную симметрию в направлении z. Тогда требуется решить уравнение внутри проводника

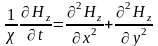, (3.58)

где  = (₀)^–1 (₀ = 410^–7 Гн/м – магнитная постоянная,  – удельная проводимость:   10⁷ Ом^–1м^–1) с соответствующими начальными и граничными условиями.