4.5. Непрерывные случайные величины

Определение 4.5. Непрерывной называют случайную величину X, функцию распределения которой F(x) можно представить в виде(x)= (4.1)

функцию р(х) называют плотностью распределения (вероятностей) случайной величины X.

Предполагают, что несобственный интеграл в представлении (4.1) сходится.

Как и прежде, для того чтобы подчеркнуть принадлежность плотности распределения случайной величине X, будем наряду с записью р(х) употреблять запись (х).

Все реально встречающиеся плотности распределения случайных величин являются непрерывными (за исключением, быть может, конечного числа точек) функциями. Следовательно, функция распределения для непрерывной случайной величины является непрерывной на всей числовой оси и в точках непрерывности плотности распределения р(х) имеет место равенство

p(x) = F'(x), (4.2)

что следует из свойств интеграла с переменным верхним пределом . Только такие случайные величины мы и будем рассматривать в дальнейшем.

Замечание 4.2. Соотношения (4.1) и (4.2), связывающие между собой функцию и плотность распределения, делают понятной следующую терминологию, часто употребляемую На практике. Функцию распределения F(x) называют интегралъным законом распределения случайной величины, а плотность распределения р(х) — дифференциальным законом распределения той же случайной величины.

На рис. 4.4 изображен типичный вид плотности распределения Р(х)

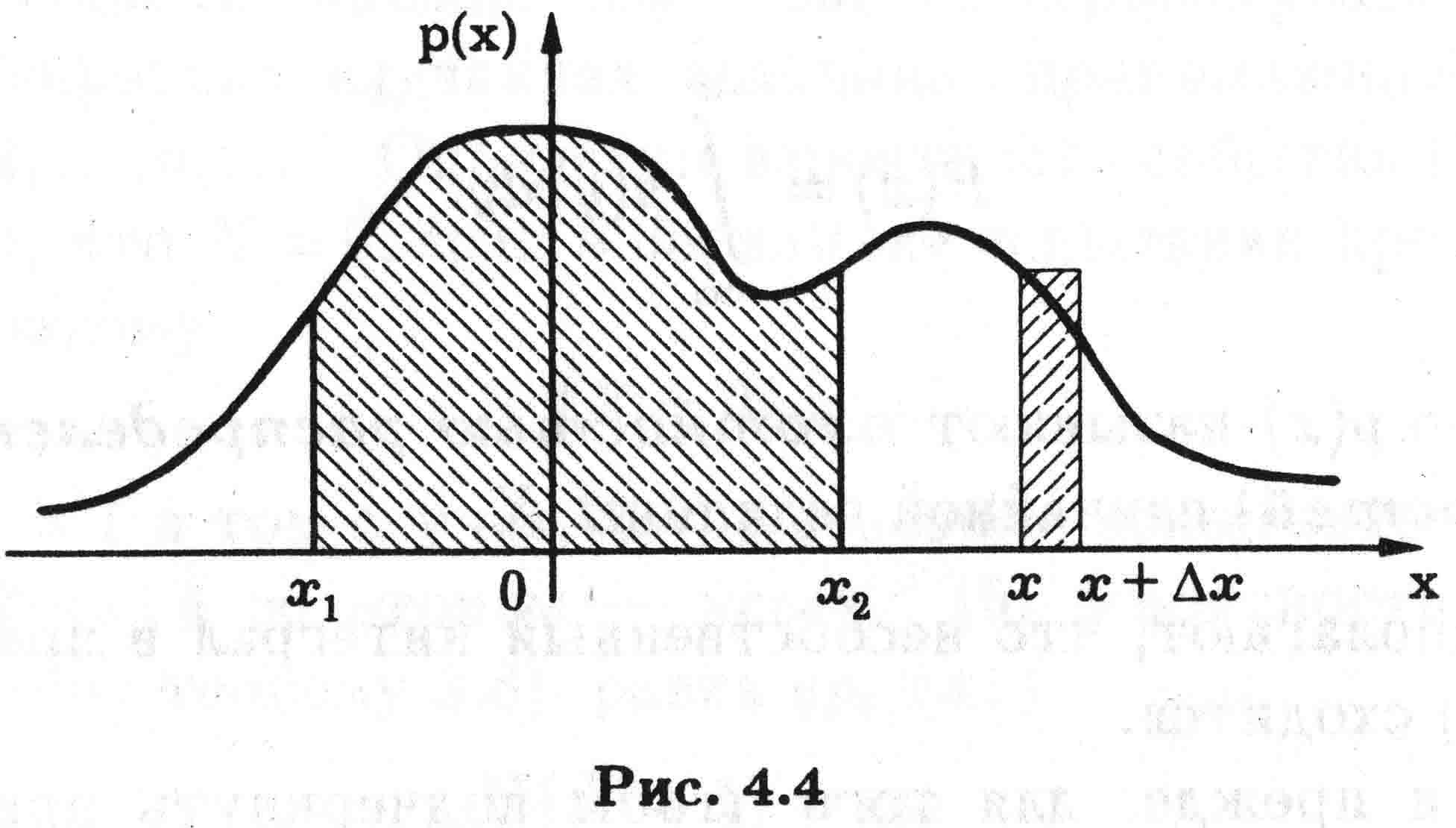
Рис.4.4

Теорема 4.2. Плотность распределения имеет свойства:

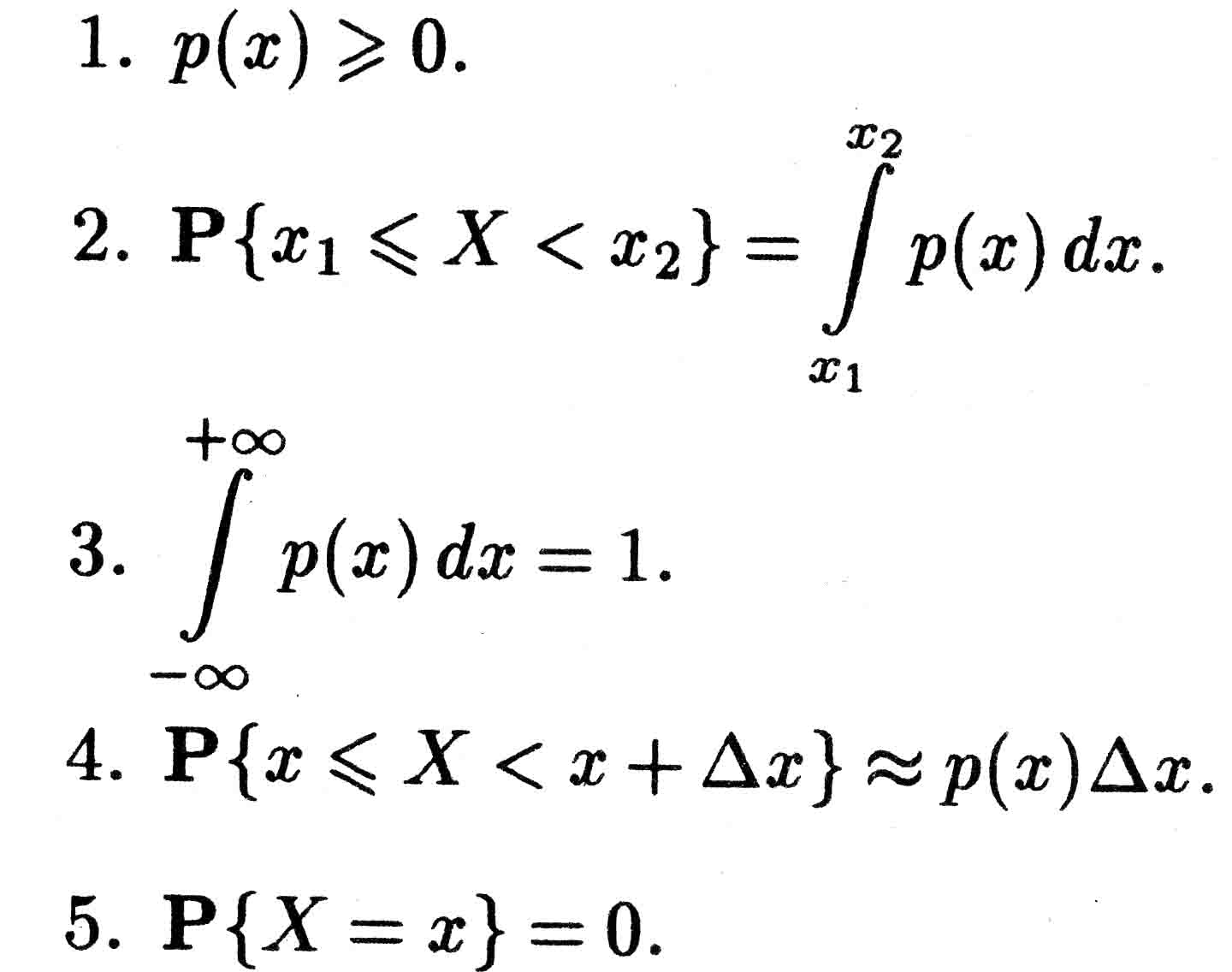
Утверждение 1 следует из того, что плотность распределения является производной от функции распределения, в силу свойства 1 функции распределения она является неубывающей функцией, а производная неубывающей функции неотрицательна.

Согласно свойству 2 функции распределения,

P{ ≤ X < х₂} = F(x₂) - F( ).

Отсюда в соответствии с определением непрерывной случайной величины и свойством аддитивности сходящегося несобственного интеграла имеем

ч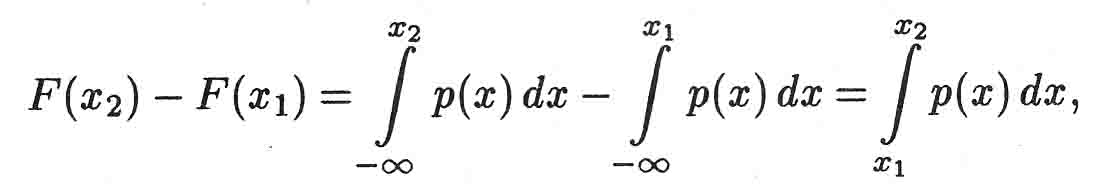 то и доказывает утверждение 2.

В частности, если х₁ , х₂ , то событие

{ < X < } является достоверным, и поэтому справедливо утверждение 3.

Согласно свойству 4 (см. теорему 4.1),

Р{x < X < х + Δх) = (x + Δх) - F(x) = ΔF(x).

Если Δх „мало" (см. рис. 4.4), то имеем

что и доказывает утверждение 4.

Наконец, поскольку в силу определения 4.5 функция распределения случайной величины есть несобственный интеграл от плотности, то она является непрерывной, что приводит нас к утверждению 5.

Замечание 4.3. В силу свойства 2 плотности распределения вероятность попадания непрерывной случайной величины в промежуток [x₁,х₂] численно равна площади криволинейной трапеции, заштрихованной на рис. 4.4.

Согласно свойству 3 площадь, заключенная под всей кривой, изображающей плотность распределения, равна единице.

В соответствии со свойством 4 вероятность попадания случайной величины X в некоторый „малый" промежуток

(х, х + Δх) практически пропорциональна Δх с коэффициентом пропорциональности, равным значению плотности распределения в точке х. Поэтому выражение р(х)Δх или p(x)dx называют иногда элементом вероятности. Можно также сказать, что непрерывная случайная величина реализует геометрическую схему с коэффициентом пропорциональности но только в „малой" окрестности точки х.

Наконец, согласно свойству 5, вероятность попадания в любую (заданную до опыта) точку для непрерывной случайной величины равна нулю.

В заключение отметим, что на практике иногда встречаются случайные величины, которые нельзя отнести ни к дискретным, ни к непрерывным случайным величинам, как показывает следующий пример.

Пример 4.4. На перекрестке стоит автоматический светофор, в котором = 1 мин горит зеленый свет, = 0,5 мин — красный, опять 1 мин — зеленый, 0,5 мин — красный и т.д. В случайный момент времени, не связанный с работой светофора, к перекрестку подъезжает автомобиль.

Пусть X — время ожидания у перекрестка. Покажем, что X не является ни дискретной, ни непрерывной случайной величиной.

Обозначим t = + = 1,5 мин цикл работы светофора. Естественно считать, что автомобиль подъезжает к перекрестку в случайный момент времени по отношению к циклу работы светофора. Тогда, с одной стороны, с вероятностью = 2/3 автомобиль проедет перекресток не останавливаясь, т.е. X принимает значение 0 с вероятностью 2/3 > 0. Поэтому X не может быть непрерывной случайной величиной. С другой стороны, на второй 0,5-минутной части цикла работы светофора время ожидания X может принять любое значение от 0 до 0,5. Значит, X не может быть также дискретной случайной величиной.

Для того чтобы лучше понять существо дела, построим функцию распределения F(x) случайной величины X. Поскольку время ожидания не может принять отрицательное значение, то F(x) = 0 для всех х < 0. Далее если 0 < х < 0,5, то событие {X < х} происходит в том случае, когда автомобиль либо попадет на первую часть цикла работы светофора (зеленый свет), либо подъедет к светофору при красном свете, но до включения зеленого света останется время, меньшее х. В соответствии с определением геометрической вероятности

Наконец, поскольку автомобиль в любом случае проведет у перекрестка не более 0,5 мин, то F(x) = 1, x>0,5

Таким образом,

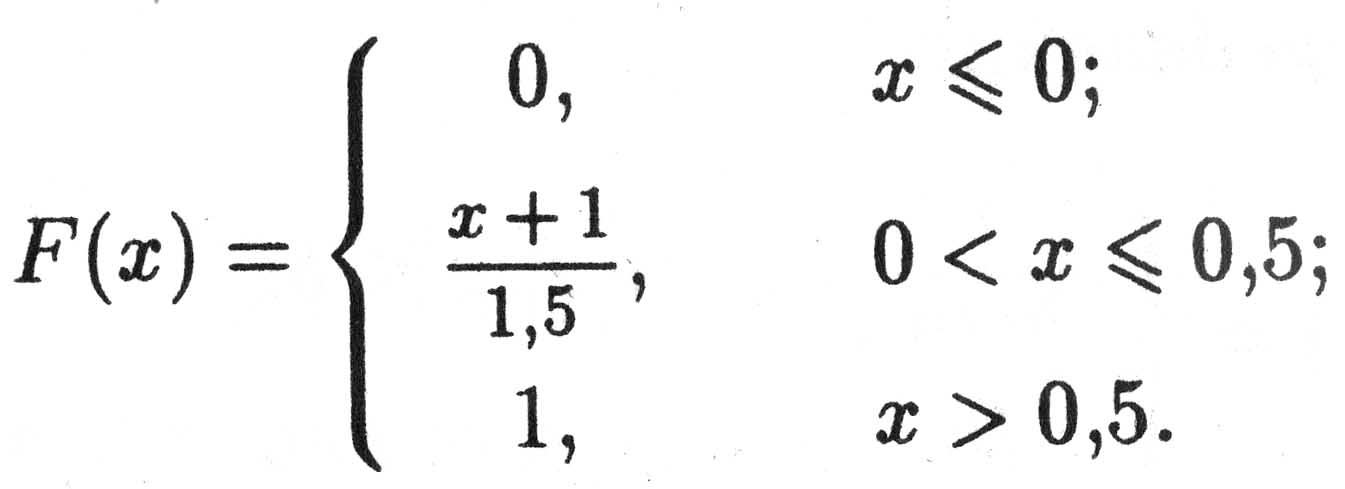
График функции распределения F(x) приведен на рис. 4.5.

Отметим, что в рассмотренном примере случайная величина X представляла собой „смесь" дискретной и непрерывной случайных величин, причем Р{Х = 0} = F(+0) - F(0) — скачку Функции распределения в точке х = 0. Можно привести и более сложные примеры, в которых случайные величины уже не являются „смесью" дискретной и непрерывной составляющих, однако эти примеры нужно отнести к разряду математических абстракций.

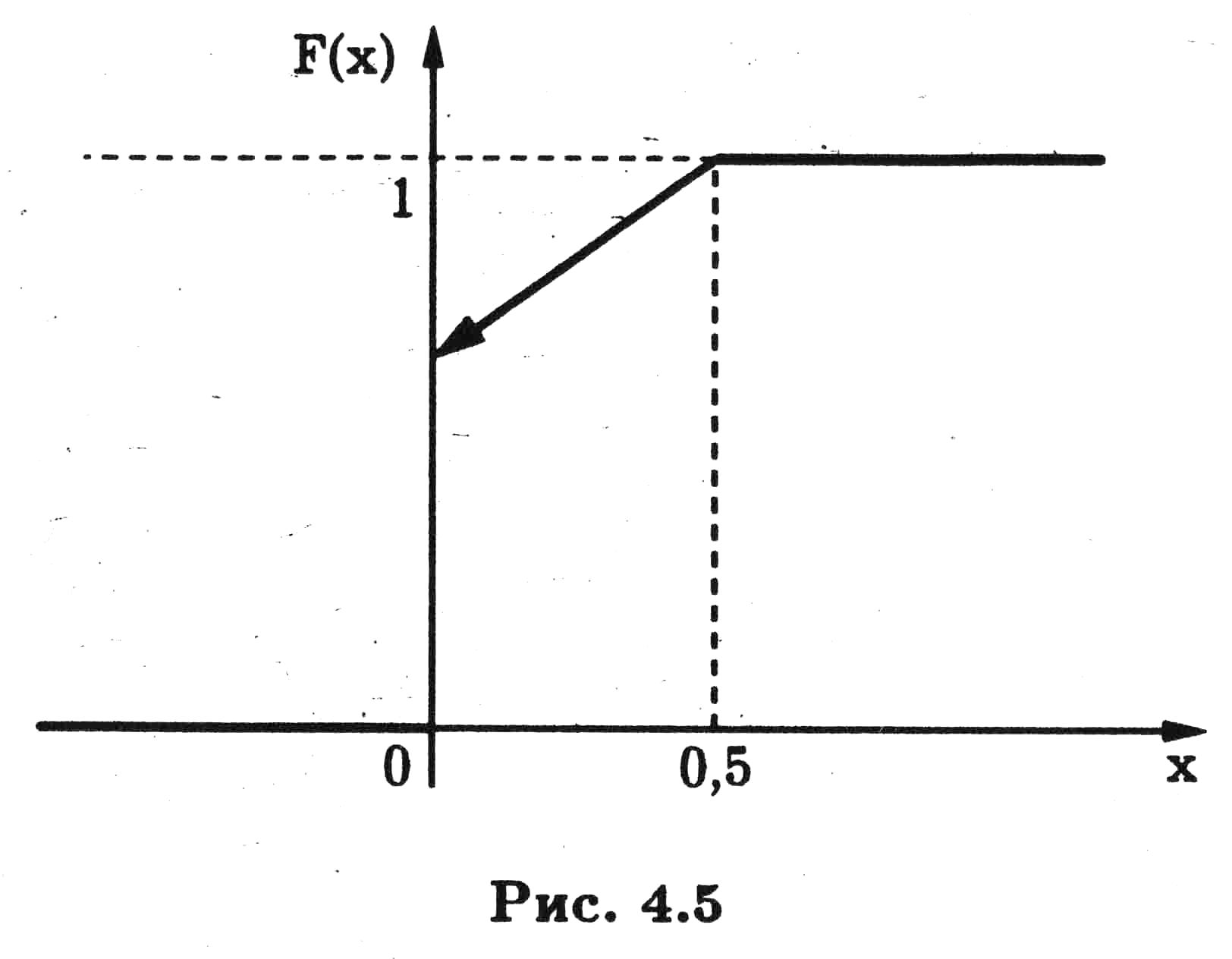
Рис.4.5