Добавил:

89135606891 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саяно-Шушенский Филиал Сибирского Федерального Университета

Предмет:

Теоретические основы электротехники

Файл:

Алехин электротехника

.pdf

Скачиваний:

Добавлен:

28.02.2024

Размер:

9.47 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 378 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

4.3. Правило переноса источника напряжения через узел

1			1	1
			1	1
	E1		E1
А	V		E E	E
А		E	Б
	2	E	2	2
	2		2	2
			E	E
				E

а)

б)

в)

Рис.4.14

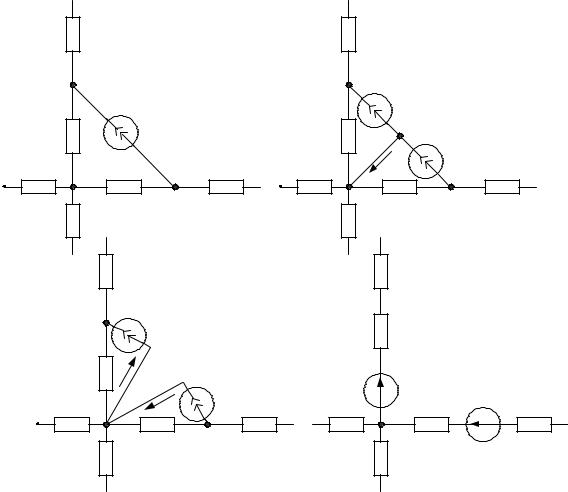
В первой ветви исходной схемы рис.4.14а включен источник напряжения E1 , направленный от узла А. Окрестность узла А, обведенная пунк-

тиром, не содержит источников напряжения. Такой узел А называют «пустой узел».

В схеме рис.4.14б в каждой ветви включены дополнительные источники E E1, направленные к узлу Б. Окрестность узла Б с источниками

напряжения обведем пунктиром и будем рассматривать как многополюсник. Если все ИН равны, то напряжения между любыми зажимами многополюсника будут равны нулю. Следовательно, узел Б можно считать «пустым узлом», эквивалентным узлу А. Значит, исходная схема рис.4.14а эквивалентна схеме рис.4.14в, в которой источник напряжения перемещен через узел во все другие ветви, присоединенные к этому узлу.

П р а в и л о

Источник напряжения можно перенести через узел во все другие ветви, присоединенные к данному узлу, без изменения токов в схеме.

4.4.Правило размножения источников тока

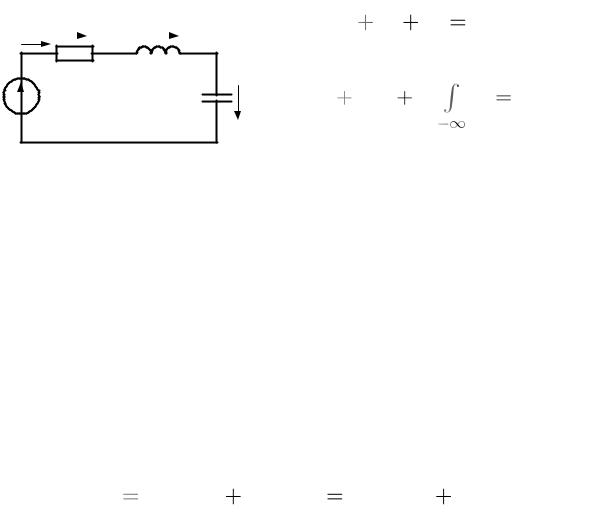
Висходной схеме рис.4.15а требуется устранить узлы 2 и 4. В идеальном источнике тока ток постоянный по величине и не зависит от внешней цепи. Последовательное соединение двух одинаковых по величине источников тока (рис.4.15б) эквивалентно одному ИТ.

Всхеме рис.4.15б соединим узлы 3 и 3’перемычкой. Ток в перемыч-

ке равен нулю, так как по первому закону Кирхгофа J J I 0.

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

Расщепим перемычку 3-3’ на две с токами J (рис. 4.15в) и преобразуем источники тока с параллельными резисторами R2 и R3 в источники

напряжения. Получим эквивалентную схему рис.4.15г, в которой устранены узлы 2 и 4.

	а)	R4				б)	R4
	а)					б)
	2					2		J
	R2			J		R2		3'		J
	R2					R2				J
	R1				R5	R1		I=0		R5
1		3	R3	4		1	3	R3		4
1			R3			1		R3		4
		R6					R6
	в)		R4			г)		R4
	в)					г)
		2		J
		2						R2
								R2
		R2	J
		R2			J
					J			JR2		JR3
		R1		J	R5	R1		JR2		JR3	R5
		R1		J	R5	R1					R5
	1		3	R3	4	1		3	R3
				R3					R3
			R6					R6

Рис.4.15

П р а в и л о

Идеальный источник тока может быть заменён несколькими равными по величине источниками тока, подключёнными параллельно всем ветвям, которые составляют контур с исходным источником тока

(рис.4.16).

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

J J J J

Рис.4.16

4.5. Контрольные вопросы

1.Что называют преобразованием или сверткой цепи ?

2.Как рассчитать эквивалентное сопротивление при последовательном соединении резисторов ?

3.Как работает делитель напряжения на резисторах ?

4.Как рассчитать эквивалентную проводимость при параллельной соединении резисторов ?

5.Как работает делитель токов на двух резисторах ?

6.Как рассчитать проводимость стороны треугольника в проебразовании звезда-треугольник ?

7.Как рассчитать сопротивление луча звезды в преобразовании тре- угольник-звезда ?

8.Как найти эквивалентную схему при последовательной соединении источников напряжения ?

9.Как найти эквивалентную схему при параллельном соединении источников тока ?

10.Как найти эквивалентную схему при параллельном соединении источников напряжения ?

11.Сформулируйте и объясните правило переноса источника напряжения через узел.

12.Сформулируйте и объясните правило размножения источников

тока.

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

Глава 5. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ТОКАХ И НАПРЯЖЕНИЯХ

5.1.Гармонические сигналы и их характеристики

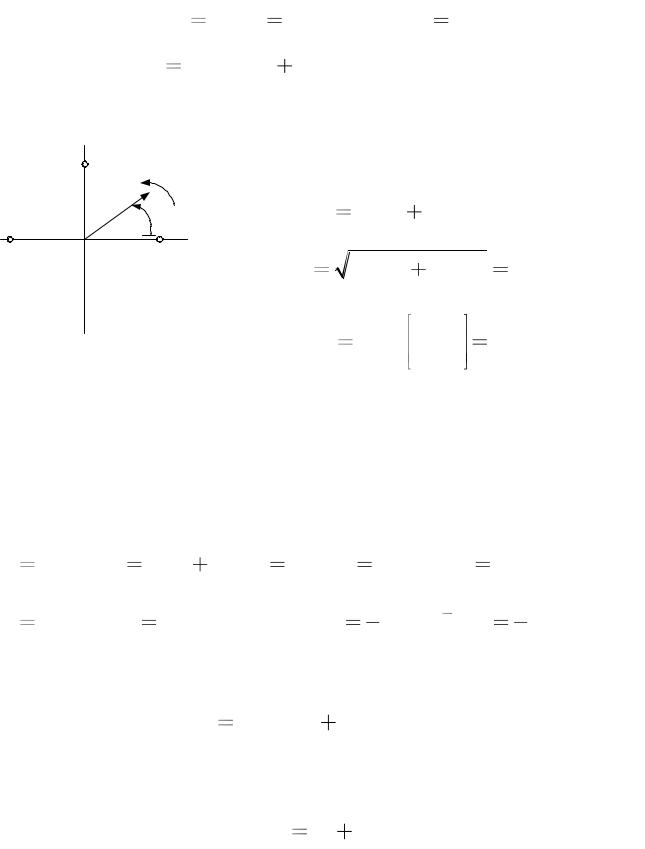
Влинейной электрической цепи процессы описываются линейными интегро-дифференциальными уравнениями, которые справедливы для любой формы сигналов. Так для цепи рис.5.1 по второму закону Кирхгофа можно составить уравнения:

i(t)	uR	(t)	L	uR uL uC e(t)	(5.1)
				uR uL uC e(t)	(5.1)

	R	L
	R
e(t)		C	uC(t)	iR
		C	uC(t)	iR
		Рис.5.1

или

	di	1		t
L				idt e(t) (5.2)
	dt		C

Для гармонического сигнала применяют упрощённый метод расчёта, не требующий решения интегро-дифференциального уравнения. Он называется символический метод расчёта цепей гармонического тока и использует параметры (символы) гармонической функции.

Г а р м о н и ч е с к и й с и г н а л

Гармоническими сигналами называют синусоидальные и косинусоидальные функции одной частоты.

В радиотехнике традиционно используют косинусоидальные функ-

ции.

В электротехнике мы будем применять синусоидальные гармонические функции. Мгновенные значения синусоидальных функций тока и напряжения записывают так:

i(t) Imsin( t I ) , u(t) Umsin( t ΨU ). (5.3)

Характеристиками (параметрами) гармонического сигнала являются угловая частота , амплитуда ( Im ,Um ) и начальная фаза ( I , U ). В

цепи гармонического синусоидального тока во всех ветвях угловая частота ω известна. Неизвестны и подлежат определению амплитуды и фазы сиг-

налов Im ,ΨI и Um ,ΨU . Каждый ток и напряжение можно охарактеризо-

вать амплитудой и начальной фазой и все расчёты вести только для амплитуд и фаз гармонической функции.

Амплитуда и фаза– это символы, характеризующие гармоническую функцию. Подставив их в общее выражение (5.3) с известной частотой ,

всегда можно найти мгновенное значение функции.

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

Пример 5.1

		0	3 1
Рассчитаны: Im	2A,	45 .Известна	10		.
Рассчитаны: Im	2A,	45 .Известна	10	c	.
				c
Находим: i( t )	2 sin(103t	450 ) А.

5.2. Оператор поворота

+j	j
	+
	1
	Ф
-1	1 +1

-j

Рис.5.2

Рассмотрим комплексную				экспоненци-
альную функцию e jΦ .
По формуле Эйлера
	e jΦ	cosΦ	j sinΦ		(5.4)
Модуль этой комплексной величины

	e jΦ	cos2 Φ	sin2 Φ	1	(5.5)
Аргумент
arg e jΦ		arctg	sinΦ	Φ	(5.6)
arg e jΦ		arctg	cosΦ	Φ	(5.6)
			cosΦ

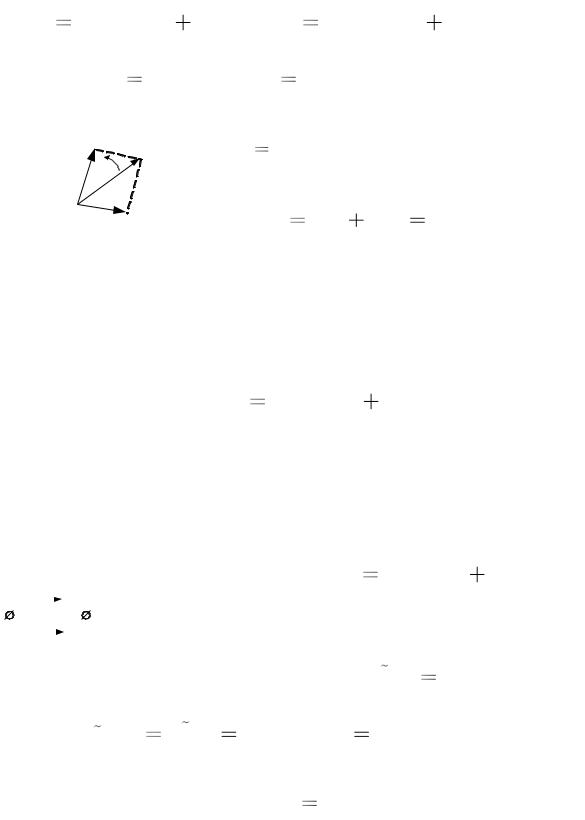
На комплексной плоскости (рис. 5.2) комплексная функция (5.4) изображается вектором единичной длины, повернутым относительно оси +1 против часовой стрелки на угол Φ . Функ-

цию e jΦ называют оператором поворота, так как при изменении Φ , изображающий ее вектор поворачивается на комплексной плоскости

(рис.5.2).

Найдем положения единичного вектора для нескольких значений Φ :

Φ0 , e

Φπ , e

j00

j1800


cos 0	j sin 0 1, Φ	π		,	e j900	j ,
		2
						.(5.7)
			π
-1,	Φ			,	e j900	j
		2

5.3. Символическое представление гармонической функции

Рассмотрим гармоническую функцию тока
i(t) Imsin( t		I ) ,	(5.8)
в которой: Im - амплитуда; - угловая частота; I			- начальная фа-
за.
Обозначим текущую фазу гармонической функции
( t )	t	I	(5.9)

Подставим текущую фазу в оператор поворота и получим вращающийся вектор:

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

	65
e j ( t )	cos ( t )	j sin ( t ).	(5.10)
Умножим оператор поворота на амплитуду Im и получим			комплекс-

ную функцию времени для тока:

i ( t ) I	m	e j ( t )	I	m	cos ( t )	jI	m	sin ( t ) (5.11).
	m			m			m

В расчетах мы ищем мгновенное значение тока, которое равно мнимой части комплексной функции времени:

i(t) Imsin( t

I )

Im sin ( t ) Jm i ( t ) .

(5.12)

Следовательно, вычислив комплексную функцию времени, мы всегда сможем найти мгновенное значение гармонической функции.

Введем важные определения составляющих комплексной функции времени

i ( t )

e j ( t )

e j( t

I )

e j I e j t

(5.13).

Здесь: I

e j I

- комплексная амплитуда

(КА) гармонической

функции, не зависит от времени и является «символом» гармонической функции;

	Ime	j I	Im	- модуль комплексной амплитуды, амплитуда гармо-



нической функции;
I		- фаза комплексной амплитуды, равная начальной фазе гармо-
нической функции;

e j t - оператор поворота.

Для обозначения комплексной амплитуды мы будем применять подчеркивание буквы Im .

Построим вращающийся вектор, отображающий функцию i ( t )

на

комплексной

плоскости

(рис.5.3).

момент

Ime

j I

Im cos I

j Im sin I .

момент

t1получим

e j I e j t1

. При этом вектор повернется на угол t .

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

Рис.5.3
С д е л а е м в ы в о д ы :
1. Гармоническая функция i(t) Imsin( t	I ) представляется на
комплексной плоскости вектором, вращающимся с частотой . Длина
вектора Im , начальная фаза I , текущая фаза ( t )		t	I .

2. Проекция вектора на ось +j даёт гармоническую синусную функ-

цию.

3. Векторы гармонических функций одной частоты вращаются с одинаковыми угловыми скоростями и их положение относительно друг друга неизменно и соответствует моменту t 0 . Поэтому расчёт комплексных амплитуд тока и напряжения полностью определяет режим цепи

влюбой момент времени.

5.4.Формы записи комплексной амплитуды (КА)

Комплексную амплитуду можно записать в трех формах:

1.	A	A e j - показательная форма;
	m	m
2.	Am	Am cos	jAm sin - тригонометрическая форма;
3.	Am	a jb - алгебраическая форма.

Впоказательной форме удобно выполнять умножение и деление комплексных амплитуд. В алгебраической форме делают сложение и вычитание КА.

Впроцессе вычислений часто приходится делать переход от алгебраической формы записи КА к показательной.

Пусть задано: Am a jb .

Находим модуль комплексной амплитуды

A	a jb	a2	b2	(5.14)

m

и фазу

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

67
arctg	b	(	0	) .	(5.15)
arctg		(		) .	(5.15)
	a

В формуле (5.15) для векторов КА, расположенных во втором и тре-

тьем квадранте комплексной плоскости, к значению arctg ba надо при-

бавить или вычесть .

В результате получим:


								A			a2	b2 e j .		(5.16)
									m
П р и м е р 5 . 2
Дано: Am					1		j1.

Находим:				Am			1 1			2 ,
	arctg(				1	)	450			1800		2250 ,
	arctg(				1	)	450			1800		2250 ,
					1
A			e j2250 .
A		2	e j2250 .
m
П рим ер 5 . 3
Полезные формулы:
П р о и з в е д е н и е к о м п л е к с н о - с о п р я ж е н н ы х ч и с е л :
					( a		jb )( a			jb )		a2	b2 .	(5.17)

И з б а в л е н и е о т к о м п л е к с н о г о ч и с л а в з н а м е н а т е л е

1	a jb	a	jb	(5.18)

a jb ( a jb )( a jb )		a2	b2
a jb ( a jb )( a jb )		a2	b2

П рим ер 5 . 4

Дано мгновенное значение тока i( t ) 20 sin( t

Найти комплексную амплитуду.

Запишем комплексную функцию времени:

i ( t ) 20e j( t 45o ) 20e j45o e j t .

Находим комплексную амплитуду: Im 20e j45o

45o ).

В а ж н о е т р е б о в а н и е

Для правильного учёта фаз все исходные гармонические функции следует преобразовывать к одному виду, а именно к синусу:

cos( t

)

sin( t

900 )

(5.19)

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

5.5. Сложение гармонических функций одной частоты

Пусть

даны

два

гармонических

напряжения одной

частоты

u1( t ) Um1 sin( t

1 ) и u2 ( t )

Um2 sin( t

2 ).

От мгновенных значений напряжений перейдем к комплексным ам-

плитудам U

e j 1

и U

e j 2 .

На

комплексной плоскости (рис.5.4) ком-

Um2

плексные амплитуды задают для момента време-

ни t

положения вращающихся

векторов,

изображающих гармонические функции.

Сложим комплексные амплитуды:

Ume j .

(5.20)

Um1

Полученная комплексная амплитуда опре-

деляет положение результирующего

вектора

суммы двух гармонических функций.

Рис.5.4

От комплексной амплитуды перейдем к мгновенному

значению

суммы:

u( t )

Um sin( t

) .

(5.21)

Важное замечание

Сложение комплексных амплитуд возможно только для функций одной частоты, когда изображающие вектора вращаются с одной скоростью.

5.6. Гармонический ток и напряжение в резисторе

i(t)

Гармонический ток i( t )

Im sin( t

I ) проходит

через резистор (рис.5.5). Найти напряжение

на резисторе

u(t).

u(t)

Вместо мгновенного значения тока возьмем комплекс-

Рис.5.5

ную функцию времени для тока

i ( t )

j I

j t

Находим комплексную функцию времени для напряжения:

( t ) Ri ( t )

e j I e j t

e j U e j t

(5.22)

Разделим уравнение (5.22) на e j t и получим:

e j U

e j I .

(5.23)

В итоге получаем следующие выражения

для

гармонического тока

и напряжения на резисторе:

для комплексных амплитуд напряжения и тока на резисторе:

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

			69
U		mR	RIm ;	(5.24)

для модулей (амплитуд):
	UmR		RIm ;	(5.25)
для фаз:
	U		I .	(5.26)
В формуле (5.23) активным сопротивлением цепи называют R .
После расчета комплексной амплитуды находим мгновенное значе-
ние напряжения на резисторе:
uR ( t )			RIm sin( t	I ).

Векто рная диагр амма

+
+
	j				UmR
		Im			UmR
		Im				U
						U
				I
			Рис.5.6+1

Векторной диаграммой называют совокупность векторов напряжений и токов, построенных из начала комплексной плоскости с соблюдением взаимной ориентации.

На рис.5.6 показана векторная диаграмма тока и напряжения на резисторе.

В а ж н о е	п р а в и л о :			напряжение на резисторе совпадает по
фазе с током ( U		I ) и амплитуда UmR			RIm .
П рим ер 5 . 5 .
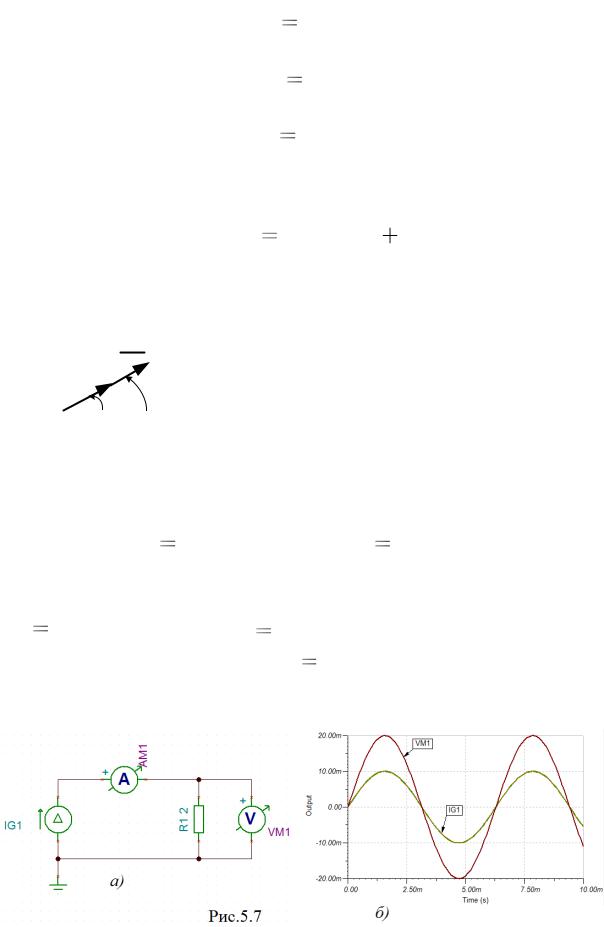
В схеме рис.5.7а с источником гармонического тока с амплитудой
Jm 10 мА и	с частотой		f	159,155 Гц рассчитать мгновенное зна-
чение напряжения на резисторе				R1 2Ом .	Выполнить моделирование
схемы рис.5.7а и сравнить			полученные графики рис.5.7б с результатами
расчета.

В.А. Алехин. Электротехника. Мультимедийный курс лекций. 2016

<<< < Предыдущая 1 2 3 4 5 6 78 / 378 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Теоретические основы электротехники

#
28.02.20242.81 Mб0Laboratornaya_rabota.docx
#
28.02.2024487.27 Кб0Mironenko_RGZ_1_TOE.docx
#
28.02.20243.19 Mб0Otvety_TOE.docx
#
28.02.2024137 Кб0VAFa_05_09.xlsx
#
28.02.20241.42 Mб1zadaniya-neti (1).pdf
#
28.02.20249.47 Mб1Алехин электротехника.pdf
#
28.02.20241.42 Mб0зад. 5.2 (1 часть).pdf
#
28.02.202414.57 Кб0Защита.docx
#
28.02.2024700.67 Кб0магнитные цепи.pdf
#
28.02.2024946.75 Кб0несинусоидальные цепи.docx
#
28.02.20243.68 Mб0практикум СФУ.pdf

	а)	R4				б)	R4
	а)					б)
	2					2		J
	R2			J		R2		3'		J
	R2					R2				J
	R1				R5	R1		I=0		R5
1		3	R3	4		1	3	R3		4
1			R3			1		R3		4
		R6					R6
	в)		R4			г)		R4
	в)					г)
		2		J
		2						R2
								R2
		R2	J
		R2			J
					J			JR2		JR3
		R1		J	R5	R1		JR2		JR3	R5
		R1		J	R5	R1					R5
	1		3	R3	4	1		3	R3
				R3					R3
			R6					R6

	а)	R4				б)	R4
	а)					б)
	2					2		J
	R2			J		R2		3'		J
	R2					R2				J
	R1				R5	R1		I=0		R5
1		3	R3	4		1	3	R3		4
1			R3			1		R3		4
		R6					R6
	в)		R4			г)		R4
	в)					г)
		2		J
		2						R2
								R2
		R2	J
		R2			J
					J			JR2		JR3
		R1		J	R5	R1		JR2		JR3	R5
		R1		J	R5	R1					R5
	1		3	R3	4	1		3	R3
				R3					R3
			R6					R6

	а)	R4				б)	R4
	а)					б)
	2					2		J
	R2			J		R2		3'		J
	R2					R2				J
	R1				R5	R1		I=0		R5
1		3	R3	4		1	3	R3		4
1			R3			1		R3		4
		R6					R6
	в)		R4			г)		R4
	в)					г)
		2		J
		2						R2
								R2
		R2	J
		R2			J
					J			JR2		JR3
		R1		J	R5	R1		JR2		JR3	R5
		R1		J	R5	R1					R5
	1		3	R3	4	1		3	R3
				R3					R3
			R6					R6