1.7. Вынужденные колебания струны с закрепленными концами

Пусть на точки струны длинны l в направлении колебаний действует непрерывно распределенная сила, плотность распределения которой равна g(t,x). В начальный момент времени точками струны придаются начальное отклонение и начальная скорость . Требуется найти отклонение u(t,x) точек струны при Эта задача сводится к следующей математической задаче. Найти функцию u(t,x), определенную на отрезке [0,l], удовлетворяющую дифференциальному уравнению

начальным условиям

и граничным условиям

Здесь

Функцию будем искать в виде суммы

где - решение задачи о свободных колебаниях струны с заданными начальными условиями и граничными условиями , а - решение задачи о вынужденных колебаниях струны с нулевыми начальными условиями. Функция определяется по формуле

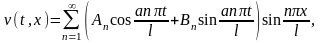
где

Функция удовлетворяет дифференциальному уравнению

начальным условиям

и граничным условиям

Функцию будем искать в виде ряда Фурье

коэффициенты которого подлежат определению. Для этого функцию разложим в ряд Фурье по синусам на отрезке [0,l]

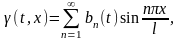
где

Функцию продифференцируем по переменным t и x дважды. Имеем

Используя, полученные ряды , получим тождество

Отсюда следует, что функция является решением дифференциального уравнения

(*)

Чтобы обеспечить выполнение начальных условий

, потребуем, чтобы функции удовлетворяли начальным условиям

(**)

Применяя преобразование Лапласа к левой и правой части уравнения (*) и учитывая условия (**), получим

то есть

Отсюда и из теоремы об умножении изображений следует, что

Таким образом, решение задачи о вынужденных колебаниях струны с закрепленными концами имеет вид

где

1.8. Общая схема метода разделения переменных (метода Фурье). Задача Штурма-Лиувилля

Выше рассматривалась задача отыскания ненулевых решений дифференциального уравнения

удовлетворяющих граничному условию Задача отыскания ненулевых решений однородных дифференциальных уравнений, удовлетворяющих однородным граничным условиям, встречается и при решении других задач математической физики. Рассмотрим, например, задачу о свободных колебаниях неоднородной струны с закрепленными концами. Это задача сводится к отысканию функции удовлетворяющего уравнению

начальным условиям

и граничным условиям

Коэффициент k(x) характеризует сопротивление струны растяжению, q(x) – сопротивление среды, - плотность струны в точке х.

Будем искать ненулевые решения нашего уравнения , удовлетворяющие граничному условию , в виде Дифференцируя дважды функцию u(t,x) по переменным t и x и подставляя полученные производные в наше уравнение , получим уравнение

Отсюда следует, что

Для определения функции Х(х) возникает следующая задача. Найти ненулевые решения дифференциального уравнения удовлетворяющие граничному условию X(0)=X(l)=0. Эта задача называется задачей Штурма- Лиувилля. Те значения для которых существуют ненулевые решения задачи называются собственными значениями, а решения Х(х) – собственными функциями задачи Штурма – Лиувилля. Вместо граничных условий могут встречаться граничные условия общего вида

где, a,b,c,d – постоянные числа или непрерывные функции от х. Различают неособый и особый случаи задачи Штурма – Лиувилля.

Неособый случай. Задача Штурма-Лиувилля называется неособой, если функции k(x), непрерывны, причем В этом случае справедливы следующие утверждения:

1. Существует бесконечно много собственных значений которым соответствуют собственные функции

2. Все собственные значения задачи положительны

3. Все собственные значения задачи простые, то есть каждому собственному значению соответствует с точностью до постоянного множителя одна собственная функция .

4. Собственные функции, отвечающие различным соответственным значениям, ортогональны с весом :

если

5. (Теорема Стеклова). Если функция f(x) имеет на отрезке [0,l] непрерывные производные до второго порядка включительно и удовлетворяет граничным условиям f(0)=f(l)=0, то она разлагается в абсолютно и равномерно сходящийся ряд Фурье

где

Утверждение 1 и 5 примем без доказательства, а утверждение 2,3,4 докажем.

Обозначим через

Тогда

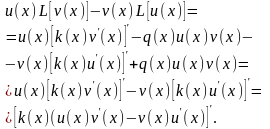
Следовательно,

Эта формула справедлива для любых непрерывно дифференцируемых на отрезке [0,l] функций k(x) и дважды непрерывно дифференцируемых функций u(x) и v(x) и называется формулой Грина.

Пусть собственные функции задачи Штурма-Лиувилля, отвечающие собственным значениям то есть

Умножим первое равенство на ,второе – на , из первого равенства вычтем второе, затем полученное равенство проинтегрируем в пределах от 0 до l. Получим

Здесь мы воспользовались формулой Грина и граничными условиями для функций и . Так как , то отсюда следует, что Утверждение 4 доказано.

Докажем, что все собственные значения простые. Допустим, что существуют две линейно независимые собственные функции отвечающие одному собственному значению . Заметим, что так как в противном случае, если то в силу единственности решения задачи Коши что противоречит определению собственных функций. Рассмотрим функцию Функция удовлетворяет начальным условиям

Начальные условия для функции совпадают с начальными условиями для функции . В силу теоремы единственности решения задачи Коши что противоречит предположению о линейной независимости собственных функций

Так как собственные функции определяются с точностью до постоянного множителя, то этот множитель можно выбрать так, чтобы то есть собственные функции можно нормировать. Пусть нормированная собственная функция, отвечающая собственному значению . Тогда

Проинтегрируем это равенство в пределах от 0 до l и воспользуемся формулой интегрирования по частям. Получим

так как Утверждения 2 и3 доказаны.

Особые случаи. Особые случаи Штурма-Лиувилля отличаются от неособого случая тем, что или функция может обращаться в ноль в некоторых точках отрезка [0,l], или уравнение рассматривается на промежутке бесконечной длинны.

Рассмотрим случай, когда функция обращается в ноль в точке х=0, причем где Это означает, что число 0 является простым корнем уравнения В этом случае справедливо следующее утверждение, которое примем без доказательства.

Теорема. Пусть функции непрерывны на отрезке [0,l], причем

Тогда, если линейно независимые решения нашего уравнения и если то

Общее решение нашего уравнения в этом случает имеет вид где Поэтому, если решение 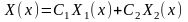удовлетворяет условию 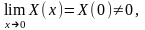то Условие позволяет найти одну из постоянных в общем решении уравнения нашего, то есть это условие заменяет одно из граничных условий задачи Штурма-Лиувилля. Поэтому задача Штурма-Лиувилля в первом особой случае ставится следующим образом.

Найти ненулевые решения уравнения

удовлетворяющие граничным условиям

. (1.44)

В особом случае условие заменяет условие в неособом случае.

Справедливы следующие утверждения о собственных значениях и собственных функциях в особом случае:

1. Существует бесконечно много собственных значений которым соответствуют собственные функции Собственные значения могут быть кратными, причем кратность каждого собственного значения конечна: каждому собственному значению может соответствовать конечное число линейно независимых собственных функций.

2. Собственные значения число может быть собственным значением.

3. Собственные функции различным собственным значениям ортогональны на отрезке [0,1], если

4. (Теорема Стеклова). Если функция f(x) имеет на отрезке [0,l] непрерывные производные до второго порядка включительно и удовлетворяет граничным условиям

если и если то функция f(x) разлагается в равномерно и абсолютно сходящийся ряд Фурье по собственным функциям задачи Штурма-Лиувилля

где

Второй особый случай задачи Штурма-Лиувилля заключается в том, что ненулевые решения основного уравнения ищутся в промежутке бесконечной длинны, например, в промежутке или В этом случае справедливо следующее утверждение, которое также примем без доказательства.

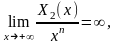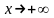Теорема. Пусть функции непрерывны в промежутке , причем и пусть линейно независимые решения основного уравнения. Тогда, если для некоторого n то если решение при растет не быстрее некоторой степенной функции то решение при растет быстрее любой степенной функции

Из этой теоремы следует, что если из общего решения уравнения (1.41) требуется найти частное решение, растущее при не быстрее некоторой степенной функции, то то есть условие для некоторого n заменяет граничное условие X(l)=0. Поэтому задача Штурма-Лиувилля во втором особом случае ставится следующим образом. Найти ненулевое решение основного уравнения , удовлетворяющие граничному условию Х(0)=0 и растущие при не быстрее некоторой степенной функции Свойства собственных значений и собственных функций во втором особом случае формулируются так же, как и свойства 1-4 в первом особом случае.