3.2. Задача Гурса
Требуется найти решение уравнения
, принимающее заданные значения на характеристиках х = х0 и у = у0:
Будем
считать, что
и
имеют непрерывные производные первого
порядка и
.
Введем, как и в случае задачи 'Коши,
Тогда основное уравнение равносильно системе трех уравнений
Отсюда, следует, что
Как и в случае задачи Коши, доказывается, что задача Гурса сводится к доказательству существования непрерывного решения системы интегральных уравнений. Как и выше, существование и единственность системы доказывается методом последовательных приближений.
3.3. Метод Римана
В этом параграфе мы выведем интегральную формулу, выражающую в явном виде искомое решение задачи Коши через начальные данные. Существование решения при этом заранее предполагается.
Наряду с дифференциальным выражением второго порядка
коэффициенты которого а и b непрерывно дифференцируемы, рассмотрим сопряженное ему дифференциальное выражение
Уравнение
называют
сопряженным с уравнением
Имеет место тождество
которое легко проверяется с помощью непосредственного дифференцирования.
Рис. 3.2.
Обозначим через Q область, ограниченную дугой PQ кривой АВ и двумя прямыми, параллельными осям и выходящими из фиксированной точки М(х0, у0) (рис. рис. 3.2). Интегрируя обе части тождества по области й и пользуясь формулой Остроградского, получим
где контур Г состоит из трех частей: характеристик QM и MP и дуги PQ.
Рассмотрим интегралы, взятые вдоль характеристик QM и MP. Так как вдоль характеристики QM меняется только у, то при интегрировании по QM получим интеграл
Интегрируя первое слагаемое по частям, будем иметь
Совершенно также найдем, что
Используя это, получим
Положим
теперь, что u
есть
решение основного уравнения ,
удовлетворяющее данным Коши , a
v—решение
однородного сопряженного уравнения
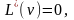удовлетворяющее
условиям
Это решение будет зависеть, конечно, от выбора точки
(х0, у0), т. е. по существу оно будет функцией пары точек. Поэтому примем обозначение v = v(x, у; х0, у0).
Имеем
на характеристике MP;
на характеристике MQ;
Решение v = v (х, у; х0, у0) однородного сопряженного уравнения , удовлетворяющее условиям , называется функцией Римана. Эта функция не зависит ни от данных Коши на l, ни от вида этой кривой. Для нее точка (х, у) играет роль аргумента, а точка (х0, у0) — роль параметра. Существование и единственность функции Римана следует .
Теперь мы получим формулу Римана
Формула Римана дает представление решения нашего уравнения для произвольных начальных данных, заданных на произвольной не характеристической кривой l, через функцию Римана v (х, у; х0, у0). Из самого способа получения формулы Римана следует, что если задача Коши имеет решение, то оно единственно.
Из формулы Римана непосредственно вытекает, что если достаточно мало изменить данные Коши на кривой l, то и решение задачи изменится на сколь угодно малую величину, т. е. решение задачи Коши непрерывно зависит от начальных данных. Из этой формулы также следует, что значение решения и в точке М зависит только от начальных данных вдоль дуги PQ кривой l, вырезаемой из / характеристиками, выходящими из точки М. Если изменить данные Коши на кривой l вне дуги PQ, сохраняя непрерывность в точках Р и Q, то решение будет меняться лишь вне криволинейного треугольника MPQ. Таким образом, каждая характеристика отделяет область, где решение осталось неизменным, от той области, где оно изменилось. Следовательно, за всякую характеристическую линию решения уравнения продолжаются неоднозначно.
Рис. 3.3.
Сделанное выше предположение о том, что прямые, параллельные осям, т. е. характеристики, пересекают линию l не более чем в одной точке, является существенным.
При невыполнении этого условия задача Коши, вообще говоря, неразрешима. Пусть, например, кривая l имеет вид, указанный на рис. 3.3. Применив метод Римана, мы можем определить значение искомой функции u(х, у) в точке М, пользуясь или криволинейным треугольником PQM, или криволинейным треугольником Q1PM. Полученные две формулы дадут, вообще говоря, в точке М разные значения для u, и, таким образом, задача Коши окажется неразрешимой.
Примеры на приложение метода Римана .
Пример:
Найти решение уравнения
,
удовлетворяющее условиям
С
помощью замены переменных
уравнение приводится к каноническому виду:
Рис. 3.4.
Прямая
у
= 1 в
новых переменных будет иметь вид
равнобочной гиперболы (рис. 3.4)
Далее из соотношений
ясно, что
Следовательно, имеем
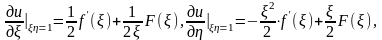а
также
Полагая
в формуле Римана а = 0,
,
,
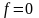получим
Обратимся
теперь к разысканию функции Римана
Согласно
общей теории, она должна удовлетворять
сопряженному уравнению
и следующими условиями на характеристиках:
Нетрудно убедиться, что функция
это и есть искомая функция Римана. Далее
получим
Возвращаясь теперь к старым переменным x и y, получим решение задачи Коши.
Пример 2. Найти решение уравнения
удовлетворяющее условиям
Чтобы решить эту задачу по методу Римана, приведем уравнение к каноническому виду, для чего составим уравнение характеристик:
Это уравнение допускает два различных интеграла
и,
следовательно, надо ввести новые
переменные
и
по
формулам
Присоединим
к этим равенствам еще одну зависимость
тогда
наше уравнение преобразуется к следующему
каноническому виду:
Рис. 3.5.
Видно, что за кривую АВ (рис. 3.5) в методе
Римана следует взять биссектрису
.
Согласно
тому же методу для решения поставленной
задачи надо найти такое
частное решение сопряженного уравнения
которое
удовлетворяло бы следующим условиям
на характеристиках
Будем
искать решение уравнения в виде
где
Тогда
для
получим
следующее уравнение:
Нетрудно
видеть, что это уравнение есть частный
случай гипергеометрического уравнения
Гаусса
при
Уравнение Гаусса допускает частное решение в виде гипергеометрического ряда
абсолютно
сходящегося при
.
Отсюда ясно, что
Следовательно,
функция
и есть искомая функция Римана.
Обращаясь теперь к нашей задаче возьмем формулу Римана и положим в ней
Тогда
и
Вычислим производные. Из формул
ясно, что
Следовательно, имеем
Дифференцируя
w по
и
и
полагая затем
,получим
Отсюда, имеем
Далее из формул
вытекает, что
Вычислим
значение функции w на биссектрисе
и
в точках Р и Q. Нетрудно видеть, что
Отсюда
также легко получаем
Принимая
теперь во внимание, что
и найдем
Возвращаясь теперь к старым переменным х и у и опустив значок у этих букв, получим решение задачи Коши для уравнения
