
- •Элементы уравнений математической физики
- •Введение
- •1. Основные уравнения математической физики
- •1.1. Уравнение колебаний струны.
- •1.2. Решение задач о колебаниях бесконечной и полуограниченной cтруны (метод Даламбера)
- •1.3. Продольные колебания стержня
- •1.4. Колебания стержня с одним закрепленным концом
- •1.5. Продольный удар груза по стержню
- •1.6. Метод Фурье решения задачи о колебаниях конечной струны с закрепленными концами
- •1.7. Вынужденные колебания струны с закрепленными концами
- •1.8. Общая схема метода разделения переменных (метода Фурье). Задача Штурма-Лиувилля
- •1.9. Уравнение колебаний мембраны.
- •1.10. Решение задачи о радиальных колебаниях круглой мембраны
- •1.11. Решение задачи о продольные колебания стержня методом Фурье
- •1.12. Уравнение распространения тепла в изотропном твердом теле.
- •1.13. Решение задачи теплопроводности бесконечного и полуограниченного стержня
- •1.14. Задача теплопроводности в бесконечном цилиндре
- •1.15. Решение задачи теплопроводности в конечном стержне
- •1.16. Решение задачи теплопроводности в однородном шаре
- •1.17. Задачи, приводящие к уравнению Лапласа
- •1.18. Общий вид уравнения эллиптического типа
- •1.19. Фундаментальные решения. Функция Грина
- •1.20. Условия разрешимости граничных задач
- •1.21. Понятие гармонической функции.
- •1. Случай пространственной области.
- •2. Случай плоской области.
- •1.22. Решение задачи Дирихле для круга методом Фурье.
- •1.23. Решение задачи Дирихле в шаре для уравнения Лапласа ( метод Фурье)
- •1.24. Задача Дирихле для одномерного и двумерного случаев.
- •2. Классификация уравнений второго порядка
- •2. I. Типы уравнений второго порядка.
- •2.2. Приведение к каноническому виду уравнения второго порядка с постоянными коэффициентами.
- •2.3. Приведение к каноническому виду уравнения второго порядка с двумя независимыми переменными.
- •3. Уравнения гиперболического типа с двумя независимыми переменными
- •3.1. Задача Коши
- •3.2. Задача Гурса
- •3.3. Метод Римана
- •Задачи электротехники
- •4.1. Дифференциальные уравнения свободных электрических колебаний
- •4.2. Телеграфное уравнение
- •4.3. Интегрирование телеграфного уравнения по методу Римана
- •5. Уравнения первого порядка
- •5.I. Квазилинейные дифференциальные уравнения с двумя независимыми переменными
- •5.2. Нелинейные дифференциальные уравнения с двумя независимыми переменными.
- •5.3. Нелинейные дифференциальные уравнения с п независимыми переменными.
- •6.2. Метод сеток решения задачи Дирихле на плоскости
- •6.3. Метод сеток решения уравнения гиперболического типа
- •6.4. Метод сеток решения уравнения параболического типа на отрезке
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
1.19. Фундаментальные решения. Функция Грина
Наряду с регулярными решениями уравнений эллиптического типа важную роль играют так называемые фундаментальные решения.
Фундаментальным
решением уравнения:
 называют
функцию Леви
называют
функцию Леви
 ,
которая при
,
которая при
 удовлетворяет
этому уравнению по координатам одной
из точек (х или
)
и зависит от координат другой точки,
как от параметров. Будем писать
удовлетворяет
этому уравнению по координатам одной
из точек (х или
)
и зависит от координат другой точки,
как от параметров. Будем писать
 или
или
 в зависимости от того, рассматриваем
ли мы как переменные, по которым
производится дифференцирование,
координаты точки
или х. Выражения
в зависимости от того, рассматриваем
ли мы как переменные, по которым
производится дифференцирование,
координаты точки
или х. Выражения
 и
и

будем
понимать как
 и
и
 .
.
Рассмотрим задачу Дирихле:
 когда
когда

где — непрерывные функции.
Предположим, что как решение u(х) этой задачи , так и функция Леви дифференциального выражения непрерывны в замкнутой области V вместе со своими первыми производными. Применив к функции u(х) формулу Грина — Стокса, получим

Если существует фундаментальное решение однородной задачи:

сопряженной
задаче Дирихле , и если это решение
непрерывно в области V вместе со своими
первыми производными, то мы можем
положить
 .
.
При этом формула для u(x) примет вид

Таким образом, если существует решение задачи Дирихле и фундаментальное решение однородной сопряженной задачи, причем в области V эти решения непрерывны вместе со своими частными производными по координатам точки , то решение задачи можно заменить отысканием фундаментального решения однородной сопряженной задачи, после чего решение задачи определится вышеприведенной формулой . Эта идея лежит в основе способа Грина решения задач Дирихле. Фундаментальное решение однородной задачи называют функцией Грина задачи Дирихле. Аналогичным путем вводится функция Грина для задачи Неймана. Рассмотрим задачу:
когда

Предположив, что u(х) —решение этой задачи, непрерывное в замкнутой области V со своими производными первого порядка, применим формулу Грина—Стокса, что даст:

Пусть
 —
фундаментальное решение однородной
задачи
—
фундаментальное решение однородной
задачи

сопряженной задаче . Если это решение непрерывно в области V вместе со своими первыми производными, то, положив = ,получим:

Таким
образом, если функция
каким-либо
образом найдена и удовлетворяет
необходимым требованиям гладкости, то
решение задачи , непрерывное вместе со
своими первыми производными в замкнутой
области V, может быть найдено с помощью
вышеприведенной формулы . Фундаментальное
решение задачи называют функцией Грина
задачи . Употребительны также названия
вторая функция Грина и характеристическая
функция Неймана. Рассмотрим две взаимно
сопряженные граничные задачи и
предположим, что их функции Грина
и
 существуют.
По определению:
существуют.
По определению:

или

Первое
граничное условие выполняется для задач
Дирихле, второе — для задач Неймана.
Предположим далее, что функции
и
имеют
производные первого порядка по координатам
точки
непрерывные в области V — х. Тогда,
фиксировав две точки
 мы можем применить формулу Грина к
функциям
мы можем применить формулу Грина к
функциям
 и
и
 в области
в области
 ,
где
,
где
 и
и
 —эллипсоидальные
окрестности точек
—эллипсоидальные
окрестности точек
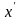 и
и
 .
Отсюда получим
.
Отсюда получим

Перейдем
к пределу при
 . Заметив, что в силу соображений,
высказанных при выводе формулы
Грина—Стокса , справедливы следующие
соотношения:
. Заметив, что в силу соображений,
высказанных при выводе формулы
Грина—Стокса , справедливы следующие
соотношения:

получим
формулу
 связывающую
функции Грина сопряженных граничных
задач. В частности, если дифференциальное
выражение
самосопряженное, то
связывающую
функции Грина сопряженных граничных
задач. В частности, если дифференциальное
выражение
самосопряженное, то
 ,
и из вышеприведенной формулы следует,
что при этом
,
и из вышеприведенной формулы следует,
что при этом

Таким образом, если для самосопряженной граничной задачи, поставленной в области , существует функция Грина , непрерывная в области вместе со своими первыми производными, то эта функция симметрична относительно точек и х.
Теоремы единственности
Положив
в формуле Грина
 и
и
 ,после
несложных выкладок придем к соотношению:
,после
несложных выкладок придем к соотношению:

Пусть
 и
и
 —два решения задачи Дирихле:
—два решения задачи Дирихле:
 когда
когда

удовлетворяющие
требованиям, при которых справедлива
формула Грина. Разность
 этих решений явится решением однородной
задачи Дирихле:
этих решений явится решением однородной
задачи Дирихле:
 когда
когда

удовлетворяющей тем же требованиям. Далее получим:

Левая часть этого соотношения неотрицательна в силу неравенства

Если
 ,
,
то
правая часть неположительна. Ввиду
непрерывности функции
 и нулевого граничного условия отсюда
следует, что в области V функция
=0,
т. е.
и нулевого граничного условия отсюда
следует, что в области V функция
=0,
т. е.
 .
Таким образом, задача Дирихле при
соблюдении нашего условия имеет не
более одного решения, непрерывного в
области вместе со своими производными
первого порядка. Проводя доказательство
этой теоремы единственности другим
путем, можно показать, что требование
непрерывности производных решения в
замкнутой области V является излишним,
достаточно требовать непрерывности
самого решения.
.
Таким образом, задача Дирихле при
соблюдении нашего условия имеет не
более одного решения, непрерывного в
области вместе со своими производными
первого порядка. Проводя доказательство
этой теоремы единственности другим
путем, можно показать, что требование
непрерывности производных решения в
замкнутой области V является излишним,
достаточно требовать непрерывности
самого решения.
Рассмотрим задачу Неймана:
когда

Предположим,
что
 —
два решения задачи, удовлетворяющие
требованиям, при которых к ним может
быть применена формула Грина. Разность
явится решением однородной задачи:
когда
—
два решения задачи, удовлетворяющие
требованиям, при которых к ним может
быть применена формула Грина. Разность
явится решением однородной задачи:
когда

Применив к разности вышеприведенную формулу, получим

Если

то, как легко видеть из этого интегрального соотношения, должно быть

в
силу чего наша задача примет вид:
 когда
когда

Отсюда
следует, что если при выполнении полученых
выше неравенств хотя бы одна из функций
g и с неравна нулю тождественно, то
=
0. В силу непрерывности функции
,
также следует, что
= 0, если хотя бы одно из неравенств
является точным. Если же ни одно из этих
дополнительных условий не имеет места,
то из соотношений вытекает, что
= const. Таким образом, задача Неймана при
 и выполнении полученых условий имеет
не более одного решения, непрерывного
в области V вместе со своими производными
1-го порядка. При g = 0 решения задачи
Неймана не могут отличаться более, чем
на постоянное слагаемое. Если хотя бы
одно из неравенств является точным,
либо функция с
отлична от
тождественного нуля, то эта постоянная
равна нулю.
и выполнении полученых условий имеет
не более одного решения, непрерывного
в области V вместе со своими производными
1-го порядка. При g = 0 решения задачи
Неймана не могут отличаться более, чем
на постоянное слагаемое. Если хотя бы
одно из неравенств является точным,
либо функция с
отлична от
тождественного нуля, то эта постоянная
равна нулю.
Задачи для самостоятельного решения.
1. Показать, что если задача Дирихле имеет не более одного решения, допускающего применение формулы Грина, то и сопряженная ей задача имеет не более одного такого решения.
2.
Показать, что самосопряженная задача
Дирихле имеет не более одного решения,
допускающего применение формулы Грина,
если
 ,
а самосопряженная задача Неймана, если,
кроме того, g > 0.
,
а самосопряженная задача Неймана, если,
кроме того, g > 0.
