
- •Элементы уравнений математической физики
- •Введение
- •1. Основные уравнения математической физики
- •1.1. Уравнение колебаний струны.
- •1.2. Решение задач о колебаниях бесконечной и полуограниченной cтруны (метод Даламбера)
- •1.3. Продольные колебания стержня
- •1.4. Колебания стержня с одним закрепленным концом
- •1.5. Продольный удар груза по стержню
- •1.6. Метод Фурье решения задачи о колебаниях конечной струны с закрепленными концами
- •1.7. Вынужденные колебания струны с закрепленными концами
- •1.8. Общая схема метода разделения переменных (метода Фурье). Задача Штурма-Лиувилля
- •1.9. Уравнение колебаний мембраны.
- •1.10. Решение задачи о радиальных колебаниях круглой мембраны
- •1.11. Решение задачи о продольные колебания стержня методом Фурье
- •1.12. Уравнение распространения тепла в изотропном твердом теле.
- •1.13. Решение задачи теплопроводности бесконечного и полуограниченного стержня
- •1.14. Задача теплопроводности в бесконечном цилиндре
- •1.15. Решение задачи теплопроводности в конечном стержне
- •1.16. Решение задачи теплопроводности в однородном шаре
- •1.17. Задачи, приводящие к уравнению Лапласа
- •1.18. Общий вид уравнения эллиптического типа
- •1.19. Фундаментальные решения. Функция Грина
- •1.20. Условия разрешимости граничных задач
- •1.21. Понятие гармонической функции.
- •1. Случай пространственной области.
- •2. Случай плоской области.
- •1.22. Решение задачи Дирихле для круга методом Фурье.
- •1.23. Решение задачи Дирихле в шаре для уравнения Лапласа ( метод Фурье)
- •1.24. Задача Дирихле для одномерного и двумерного случаев.
- •2. Классификация уравнений второго порядка
- •2. I. Типы уравнений второго порядка.
- •2.2. Приведение к каноническому виду уравнения второго порядка с постоянными коэффициентами.
- •2.3. Приведение к каноническому виду уравнения второго порядка с двумя независимыми переменными.
- •3. Уравнения гиперболического типа с двумя независимыми переменными
- •3.1. Задача Коши
- •3.2. Задача Гурса
- •3.3. Метод Римана
- •Задачи электротехники
- •4.1. Дифференциальные уравнения свободных электрических колебаний
- •4.2. Телеграфное уравнение
- •4.3. Интегрирование телеграфного уравнения по методу Римана
- •5. Уравнения первого порядка
- •5.I. Квазилинейные дифференциальные уравнения с двумя независимыми переменными
- •5.2. Нелинейные дифференциальные уравнения с двумя независимыми переменными.
- •5.3. Нелинейные дифференциальные уравнения с п независимыми переменными.
- •6.2. Метод сеток решения задачи Дирихле на плоскости
- •6.3. Метод сеток решения уравнения гиперболического типа
- •6.4. Метод сеток решения уравнения параболического типа на отрезке
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
6.2. Метод сеток решения задачи Дирихле на плоскости
Пусть область D на плоскости xy ограничена
кусочно-гладким
контуром С (рис. 6.1). Требуется найти
функцию 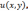 имеющую во внутренних точках области
D
непрерывные частные производные до
второго порядка включительно,
удовлетворяющую в области D
дифференциальному уравнению
имеющую во внутренних точках области
D
непрерывные частные производные до
второго порядка включительно,
удовлетворяющую в области D
дифференциальному уравнению
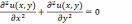
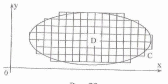
Рис. 6.1.
И
граничному условию  где
где
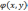 непрерывная функция, заданная в точках
контура С.
непрерывная функция, заданная в точках
контура С.
Решение этой задачи по методу сеток заключается в следующем. Пусть задано некоторое h>0. Проводятся прямые x=xi, y=yk строится контур Ch максимально приближенное к контуру С, через Dh ,обозначается область, состоящая из узловых точек (xi, yk),лежащих внутри контура Сh. Частные производные, входящие в уравнение , в точках (xi, yk) заменяются по формулам


После
такой замены наше уравнение принимает
вид
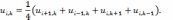
Значение
функции 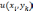 в точках
в точках 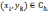 принимаются равными значениями функции
принимаются равными значениями функции
 в точках
ближайшим к точкам
в точках
ближайшим к точкам 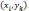 Таким образом, исходная задача Дирихле
сводится к следующей: найти значение
функции
Таким образом, исходная задача Дирихле
сводится к следующей: найти значение
функции  в точках области Dh,удовлетворяющей
системе линейных уравнений имеет
единственное решение. Для решения этой
системы применяется метод итераций или
метод Зейделя.
в точках области Dh,удовлетворяющей
системе линейных уравнений имеет
единственное решение. Для решения этой
системы применяется метод итераций или
метод Зейделя.
Метод
итераций решения системы заключается
в следующем: начальное приближение 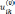 выбирается произвольным, например,
можно во всех точках
выбирается произвольным, например,
можно во всех точках 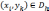 положить
положить
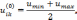
где
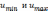 -
наименьшее и наибольшее значения функции
в узловых точках контура
-
наименьшее и наибольшее значения функции
в узловых точках контура  .
Последующие приближения вычисляются
по формулам
.
Последующие приближения вычисляются
по формулам
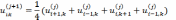
где
j=
0,1,2,… .Вычисления ведутся до тех пор,
пока неравенство
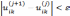
в
формуле используются уже вычисленные
 то есть
то есть
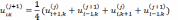
Как
правило, метод Зейделя дает более быструю
сходимость. Для получения более точного
решения все вычисления повторяются при
h=h/2.
Дробление шага проводится до тех пор,
пока значения 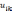 не будет отличаться от вычисленных на
предыдущем этапе менее заданного
не будет отличаться от вычисленных на
предыдущем этапе менее заданного 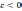 .
.
6.3. Метод сеток решения уравнения гиперболического типа
Пусть
отрезок ограничен на оси х
точками 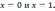 Требуется найти непрерывную в области
Требуется найти непрерывную в области
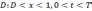 функцию
функцию 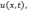 удовлетворяющую
дифференциальному уравнению
удовлетворяющую
дифференциальному уравнению
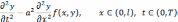
со следующими начальными
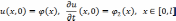
граничными условиями

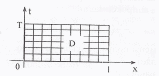
Рис. 6.2.
Решение
этой задачи по методу сеток заключается
в следующем. В области D
(рис. 6.2) проведем два семейства прямых
 для некоторых заданных
для некоторых заданных 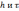 и рассмотрим всевозможные точки попарных
пересечений, то есть точки вида
и рассмотрим всевозможные точки попарных
пересечений, то есть точки вида 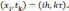 Эти точки образуют точки, являясь её
узлами. У каждого узла
Эти точки образуют точки, являясь её
узлами. У каждого узла 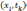 имеются четыре соседних точки
имеются четыре соседних точки  Если
все эти соседние точки также принадлежат
сетке, то узел
Если
все эти соседние точки также принадлежат
сетке, то узел 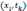 называется внутренним, в противном
случае узел называется гармоничным.
Совокупность внутренних узлов образует
множество
называется внутренним, в противном
случае узел называется гармоничным.
Совокупность внутренних узлов образует
множество  Очевидно, что точка
принадлежит
Очевидно, что точка
принадлежит  ,
если
,
если 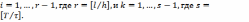 Значение искомой функции
Значение искомой функции  в узлах сетки называется сеточной
функцией
в узлах сетки называется сеточной
функцией
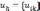 ,
приближенные значения которой мы и
будем в дальнейшем находить.
,
приближенные значения которой мы и
будем в дальнейшем находить.
Для
получения разностного уравнения заменим
частные производные второго порядка
разностными отношениями:


Частную производную по времени, входящую в начальное условие, заменим центральной разностью для обеспечения второго порядка аппроксимации
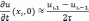
После такой замены получим искомую разностную схему, которая представляет собой следующую систему линейных алгебраических уравнений:
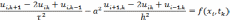

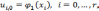



Удобно поставить в соответствие построенному разностному оператору «шаблон»- геометрическую картинку расположения узлов сетки, значения в которых связывает разностный оператор при некоторых фиксированных i и k. Для ревностного оператора нашей задачи шаблон изображен на рис. 6.3.
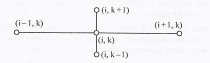
Рис. 6.3.
Для
дальнейшего рассмотрения введем понятие
слоя.
Под слоем разностной схемы понимается
совокупность точек сетки
,
лежащих на некоторой горизонтальной
(или вертикальной) прямой. Если значения
сеточной функции 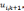 заданные на
заданные на 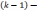 ом
слое, выражаются в явном виде через
значения этой же функции на слоях с
меньшими номерами, то такая схема
называется явной.
В противном случае схема называется
неявной.
Полученная нами разностная схема
является явной, и может быть записана
следующим образом:
ом
слое, выражаются в явном виде через
значения этой же функции на слоях с
меньшими номерами, то такая схема
называется явной.
В противном случае схема называется
неявной.
Полученная нами разностная схема
является явной, и может быть записана
следующим образом:
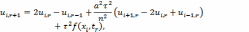

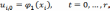
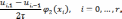
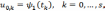
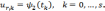
Для
аппроксимации начального условия,
заданного центральным разностным
отношением, привлечем узлы горизонтального
слоя, соответствующего  .
Промежуточные значения
.
Промежуточные значения 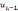 исключим, используя разностное уравнение
при
исключим, используя разностное уравнение
при 
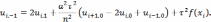
В
итоге получим следующую систему
уравнений, решая которую относительно
неизвестных 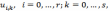 находим
сеточную функцию
находим
сеточную функцию  ,
значения которой в узлах сетки приближенно
заменяют значения искомого решения
исходного уравнения гиперболического
типа
,
значения которой в узлах сетки приближенно
заменяют значения искомого решения
исходного уравнения гиперболического
типа
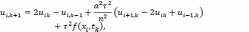
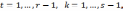
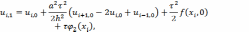

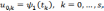

С
целью обеспечения устойчивости полученной
разностной схемы значений шагов по
времени и координате должны быть связаны
соотношением 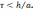 Для получения более точного решения
следует проводить дробление шага в
соответствии со сказанным в описании
решения уравнения эллиптического типа.
Для получения более точного решения
следует проводить дробление шага в
соответствии со сказанным в описании
решения уравнения эллиптического типа.
