
- •Элементы уравнений математической физики
- •Введение
- •1. Основные уравнения математической физики
- •1.1. Уравнение колебаний струны.
- •1.2. Решение задач о колебаниях бесконечной и полуограниченной cтруны (метод Даламбера)
- •1.3. Продольные колебания стержня
- •1.4. Колебания стержня с одним закрепленным концом
- •1.5. Продольный удар груза по стержню
- •1.6. Метод Фурье решения задачи о колебаниях конечной струны с закрепленными концами
- •1.7. Вынужденные колебания струны с закрепленными концами
- •1.8. Общая схема метода разделения переменных (метода Фурье). Задача Штурма-Лиувилля
- •1.9. Уравнение колебаний мембраны.
- •1.10. Решение задачи о радиальных колебаниях круглой мембраны
- •1.11. Решение задачи о продольные колебания стержня методом Фурье
- •1.12. Уравнение распространения тепла в изотропном твердом теле.
- •1.13. Решение задачи теплопроводности бесконечного и полуограниченного стержня
- •1.14. Задача теплопроводности в бесконечном цилиндре
- •1.15. Решение задачи теплопроводности в конечном стержне
- •1.16. Решение задачи теплопроводности в однородном шаре
- •1.17. Задачи, приводящие к уравнению Лапласа
- •1.18. Общий вид уравнения эллиптического типа
- •1.19. Фундаментальные решения. Функция Грина
- •1.20. Условия разрешимости граничных задач
- •1.21. Понятие гармонической функции.
- •1. Случай пространственной области.
- •2. Случай плоской области.
- •1.22. Решение задачи Дирихле для круга методом Фурье.
- •1.23. Решение задачи Дирихле в шаре для уравнения Лапласа ( метод Фурье)
- •1.24. Задача Дирихле для одномерного и двумерного случаев.
- •2. Классификация уравнений второго порядка
- •2. I. Типы уравнений второго порядка.
- •2.2. Приведение к каноническому виду уравнения второго порядка с постоянными коэффициентами.
- •2.3. Приведение к каноническому виду уравнения второго порядка с двумя независимыми переменными.
- •3. Уравнения гиперболического типа с двумя независимыми переменными
- •3.1. Задача Коши
- •3.2. Задача Гурса
- •3.3. Метод Римана
- •Задачи электротехники
- •4.1. Дифференциальные уравнения свободных электрических колебаний
- •4.2. Телеграфное уравнение
- •4.3. Интегрирование телеграфного уравнения по методу Римана
- •5. Уравнения первого порядка
- •5.I. Квазилинейные дифференциальные уравнения с двумя независимыми переменными
- •5.2. Нелинейные дифференциальные уравнения с двумя независимыми переменными.
- •5.3. Нелинейные дифференциальные уравнения с п независимыми переменными.
- •6.2. Метод сеток решения задачи Дирихле на плоскости
- •6.3. Метод сеток решения уравнения гиперболического типа
- •6.4. Метод сеток решения уравнения параболического типа на отрезке
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
1.22. Решение задачи Дирихле для круга методом Фурье.
В
полярной системе координат задача
формулируется следующим образом. Найти
функцию  ,
удовлетворяющую при r<R
дифференциальному уравнению
,
удовлетворяющую при r<R
дифференциальному уравнению


и условию
Найдем
сначала частные решения уравнения в
виде  – ненулевые функции, удовлетворяющие
условиям: X(0)
ограничено,
– ненулевые функции, удовлетворяющие
условиям: X(0)
ограничено, 

подставляя результаты дифференцирования в наше уравнение , получим

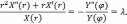
Отсюда следует, что


Уравнение
для Y(φ)
имеет решения, удовлетворяющие условию
 только при
только при  ,
и эти решения имеют вид
,
и эти решения имеют вид 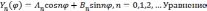

 имеет два решения линейно независимых
решения
имеет два решения линейно независимых
решения  .
Второе решение
.
Второе решение  не ограничено в точке r=0.
Поэтому полагаем
не ограничено в точке r=0.
Поэтому полагаем  Таким образом, мы получили бесконечно
много частных решений:
Таким образом, мы получили бесконечно
много частных решений:

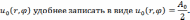
Решение поставленной задачи будем искать в виде ряда

коэффициенты
которого 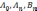 находятся таким образом, чтобы функция
находятся таким образом, чтобы функция
 удовлетворяла граничному условию .
Полагая в (3.42) r=R
получим
удовлетворяла граничному условию .
Полагая в (3.42) r=R
получим

Отсюда
следует, что  коэффициентами
Фурье для функции
коэффициентами
Фурье для функции 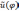 на
отрезке [0,2π]. Поэтому
на
отрезке [0,2π]. Поэтому


Подставляя
значения

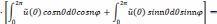



Обозначим
 и найдем сумму ряда, стоящего в квадратных
скобках формулы . Имеем
и найдем сумму ряда, стоящего в квадратных
скобках формулы . Имеем


Ряды

со
знаменателями 
 ряды
ряды

получим
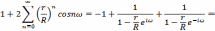


Таким образом, решение нашей задачи имеет вид

Получили другим способом решение задачи Дирихле для круга в виде интеграла Пуассона.
1.23. Решение задачи Дирихле в шаре для уравнения Лапласа ( метод Фурье)
Пусть
требуется найти функцию u(x,y,z),
гармоничную в шаре  и принимающую заданные значения
и принимающую заданные значения  В сферической системе координат задача
заключается в следующем. Найти функцию
В сферической системе координат задача
заключается в следующем. Найти функцию
 удовлетворяющую при
удовлетворяющую при 

и граничному условию

Метод
Фурье решения этой задачи заключается
в следующем: сначала ищутся частные
решения основного уравнения в виде
 где функция
где функция  ограничена в точке
ограничена в точке  ,
функция
,
функция  ограничена по переменной
ограничена по переменной  и перидична по переменной
и перидична по переменной  с периодом
с периодом  .
Функции
.
Функции  являются
собственными функциями отвечающими
собственным значениям
являются
собственными функциями отвечающими
собственным значениям  этими функциями являются сферические
функциями.
этими функциями являются сферические
функциями.


Функции
являются решениями уравнения (при 

ограниченными
в точке
.
Частные решения этого уравнения будем
искать в виде  Для определения k
получаем
Для определения k
получаем 
 которое имеет решения
которое имеет решения  Следовательно, это уравнение имеет два
линейно независимых решения
Следовательно, это уравнение имеет два
линейно независимых решения  .
Второе решение не ограничено при
.
Второе решение не ограничено при  ,
но ограничено при
,
но ограничено при  ,
поэтому оно используется для решения
внешней задачи Дирихле для шара. Для
решения внутренней задачи Дирихле для
шара. Для решения внутренней задачи
,
поэтому оно используется для решения
внешней задачи Дирихле для шара. Для
решения внутренней задачи Дирихле для
шара. Для решения внутренней задачи
Дирихле
выбираем  Таким образом, мы получили бесконечное
число частных решений уравнения
Таким образом, мы получили бесконечное
число частных решений уравнения

где n=0,1,2,.. Решение поставленной задачи будем искать в виде ряда


Коэффициенты этого ряда определяются так, чтобы выполнялось граничное условие . Полагая в решении



Отсюда следует, что

Рассмотрим
отдельно случай, когда решение задачи
Дирихле для шара не зависит от
переменной ,
то есть решение обладает осевой
симметрией. В этом случае функция
,
то есть решение обладает осевой
симметрией. В этом случае функция
является решением уравнения

и удовлетворяет граничному условию

Частные решения нашего уравнения будут вида




Первое
уравнение с помощью замены переменной
 приводится к уравнению Лежандра
приводится к уравнению Лежандра

Поэтому
уравнение имеет решения, ограниченные
в точках только при
только при  ,
и этими решениями являются функции
,
и этими решениями являются функции
 -
многочлен
Лежандра n-ого
порядка. Второе уравнение при
-
многочлен
Лежандра n-ого
порядка. Второе уравнение при 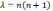 имеет
решение
имеет
решение  ограниченное
в точке
.
Следовательно, частные решения уравнения
, ограниченные при
ограниченное
в точке
.
Следовательно, частные решения уравнения
, ограниченные при  ,
имеют вид
,
имеют вид
 Дирихле в
этом случае находится в виде ряда
Дирихле в
этом случае находится в виде ряда

Коэффициенты этого ряда находятся так, чтобы выполнялось граничное условие . Полагая в равенстве , получим


Эллиптические уравнения
К этому типу относятся уравнения тепловодности
для
стационарного случая

где
искомая функция  .есть
стационарное распределение температуры
однородного тела в точке
.есть
стационарное распределение температуры
однородного тела в точке  , не зависящей от времени
, не зависящей от времени  . Наше уравнение есть уравнение Лапласа,
которое записывается еще в виде
. Наше уравнение есть уравнение Лапласа,
которое записывается еще в виде  (через оператор Лапласа
(через оператор Лапласа  ).
Для задач относящимся к плоским фигурам,
уравнение Лапласа имеет вид
).
Для задач относящимся к плоским фигурам,
уравнение Лапласа имеет вид  .
Будем рассматривать задачу Дирихле,
т.е. задачу отыскания гармонической в
области D
функции U(M)=U(x,y),
удовлетворяющей уравнению Лапласа,
непрерывной в области, включая границу
этой области , и удовлетворяющей краевому
условию
.
Будем рассматривать задачу Дирихле,
т.е. задачу отыскания гармонической в
области D
функции U(M)=U(x,y),
удовлетворяющей уравнению Лапласа,
непрерывной в области, включая границу
этой области , и удовлетворяющей краевому
условию  ,
где
,
где  - заданная непрерывная на поверхности
S
функция. Функция называется гармонической
в области D
, если в этой точке она непрерывна вместе
со своими производными до второго
порядка включительно и удовлетворяет
уравнению Лапласа. Например, для любой
плоской области, удовлетворяющей
уравнению , гармонической функцией
будет функция
- заданная непрерывная на поверхности
S
функция. Функция называется гармонической
в области D
, если в этой точке она непрерывна вместе
со своими производными до второго
порядка включительно и удовлетворяет
уравнению Лапласа. Например, для любой
плоской области, удовлетворяющей
уравнению , гармонической функцией
будет функция  (или
(или
 ),
где
),
где  ,
точки
,
точки  .
.
