1.15. Решение задачи теплопроводности в конечном стержне

Пусть в стержне длины l задано начальное распределение температур. Требуется найти температуру точек стержня при t>0. Рассмотрим сначала случай, когда на концах поддерживается нулевая температура, т.е. рассмотрим следующую задачу.

l,

t>0 дифференциальному уравнению

начальному условию

и граничным условиям

Найдем сначала ненулевые решения , удовлетворяющие только граничному условию. Эти решения будем искать в виде Дифференцируя функцию по переменным t и x дважды и подставляя результаты дифференцирования в основное уравнение получим

сюда следует, что

Задача имеет ненулевые решения только при

вид

следовательно,

поставленной задачи будем искать в виде ряда

коэффициенты которого подбираются таким образом, чтобы выполнялось начальное условие.

При t=0, получим

Рассмотрим теперь случай, когда на концах отрезка В этом случае требуется найти решение уравнения , удовлетворяющее начальному условию и граничным условиям

Эта задача сводится к предыдущей с помощью замены

неизвестной функции

Наше уравнение, удовлетворяет граничному условию и

начальному условию

,

где Аналогично решаются задачи теплопроводности конечного стержня при граничных условиях других типов.

1.16. Решение задачи теплопроводности в однородном шаре

Пусть в шаре распределение температур, и пусть в точках сферы

поддерживается нулевая температура. Мы рассмотрим частный случай этой задачи, когда начальная температура зависит лишь от расстояния точки от центра шара и не зависит от угловых координат этой точки. Поэтому и при t>0 температура в точках шара зависит лишь от расстояния этой точки от центра шара. По этой причине задачу целесообразно решать в сферической системе координат . Как известно, оператор Лапласа в сферической системе координат имеет вид

Следовательно, рассматриваемая задача заключается в следующем.

Найти функцию

Начальному условию

и граничным условиям

Условие

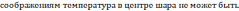
вспомогательную функцию

ренцирования в уравнение, приходим после сокращения на к следующей задаче.

Найти функцию

Решение этой задачи имеет вид

Таким образом, решение задачи теплопроводности в однородном шаре имеет вид

по формулам выше приведенным формулам.

1.17. Задачи, приводящие к уравнению Лапласа

Установившаяся температура в однородном твердом теле. В предыдущем параграфе было установлено, что уравнение распространения тепла в изотропном однородном теле в случае отсутствия источников тепла имеет вид

Допустим теперь, что температура в каждой точке (х, у, z) внутри тела установилась, т. е. что она не меняется с течением времени. Тогда и наше уравнение примет вид

Таким образом, уравнению Лапласа удовлетворяет темпера- тура и (х, у, z), установившаяся в однородном теле. Для определения и(х, y, z) теперь не надо уже задавать начальное распределение температуры (начальное условие), а достаточно задать одно граничное условие, не зависящее от времени. Задача определения решения уравнения Лапласа по его значениям на границе рассматриваемой области называется задачей Дирихле. Задача определения решения уравнения Лапласа, удовлетворяющего граничному условию , называется задачей Неймана. Потенциальное движение несжимаемой жидкости. Рассмотрим установившееся движение несжимаемой жидкости. Пусть движение жидкости невихревое или, иначе говоря, потенциальное, т. е. скорость v (х, у, z) есть потенциальный вектор v=grad . Для несжимаемой жидкости плотность ρ постоянна, и из уравнения неразрывности имеем div =0.

Далее получим

или

т.е. потенциал скорости удовлетворяет уравнению Лапласа.