4. Задачи электротехники

4.1. Дифференциальные уравнения свободных электрических колебаний

При прохождении по проводу электрического тока вокруг него образуется электромагнитное поле, которое вызывает изменения как силы тока, так и величины напряжения. Благодаря этим изменениям в проводе возникает определенный колебательный процесс, изучением которого мы и займемся. Проведем ось Ох вдоль оси провода, а начало координат поместим в один из его концов; длину провода обозначим через l. Сила тока i и напряжение v в какой-нибудь точке провода будут функциями абсциссы х и времени t. Величины i и v связаны между собой некоторыми дифференциальными уравнениями с частными производными 1-го порядка. При выводе этих уравнений мы будем предполагать, что емкость, активное сопротивление, самоиндукция и утечка распределены вдоль провода непрерывно и равномерно, и что постоянные С, R, L и G, их характеризующие, рассчитаны на единицу длины провода.

Рассмотрим часть провода, заключенную между двумя сечениями х = х₁ и х=х₂. Применяя закон Ома к этой части провода, будем иметь

Так как, с другой стороны

то имеет место равенство

из которого, в силу произвольности х₁ и х₂, следует, что

Количество электричества, протекающего через рассматриваемый участок (х₁, х₂) провода за единицу времени

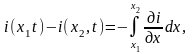
равно сумме количества электричества, необходимого для зарядки этого участка провода, и количества электричества, теряющегося вследствие несовершенства изоляции:

Таким образом,

откуда

4.2. Телеграфное уравнение

Используя результаты предыдущего раздела можно

получить:

Аналогично выводится дифференциальное уравнение

которому удовлетворяет сила тока i. Таким образом, получим, что напряжение v и сила тока i удовлетворяют одному и тому же дифференциальному уравнению

где

Это уравнение называют телеграфным уравнением. Если ввести новую функцию u(х, t), положив

то уравнение примет более простую форму:

где

4.3. Интегрирование телеграфного уравнения по методу Римана

Применим метод Римана к нахождению решения телеграфного уравнения, удовлетворяющего начальным условиям

Прежде всего преобразуем это уравнение к каноническому виду, введя новые независимые переменные £ и г] по формулам

Тогда уравнение примет вид

Рис. 4.1.

Прямая t = 0 в новых переменных будет биссектрисой (рис. 4.1): Далее, можно записать

откуда следует, что

или, в силу начальных условий , имеем

а также

Полагая в формуле Римана а = 0, b = 0, f= 0 получим

Найдем теперь функцию Римана . Она должна удовлетворять сопряженному уравнению

и обращаться на характеристиках MP и MQ в единицу. Будем искать решение уравнения в виде

Подставив это выражение в уравнение для ν и обозначив через λ корень , найдем, что функция v удовлетворяет обыкновенному дифференциальному уравнению

частным решением, которого является функция Бесселя нулевого порядка:

Тогда v=J₀(λ) получим решение уравнения, которое имеет на

характеристиках ξ=ξ₀ , η=η₀ значение 1, так как здесь λ=0. И

_{Вычисляя}

_{Получим, используя}

В старых координатах имеем:

где