1.13. Решение задачи теплопроводности бесконечного и полуограниченного стержня

а) Пусть в стержне бесконечной длинны задано начальное распределение температур. Требуется найти температуру в любой точке в любой момент времени Это означает, что требуется найти решение дифференциального уравнения

удовлетворяющее начальному условию

Пусть преобразования Фурье по переменной х функций ,

тогда

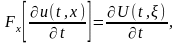
Применяя преобразование Фурье к левой и правой части основного уравнения и начального условия , приходим к следующей задаче. Найти решение дифференциального уравнения

удовлетворяющее начальному условию

Решение этой задачи имеет вид Искомая функция находится с помощью обратного преобразования Фурье:

или

где

то есть

Вычислим интеграл . Имеем

Функция - четная, а функция - нечетная по переменной . Поэтому Следовательно В последнем интеграле сделаем замену переменной и обозначим получим

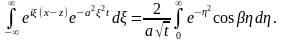
Положим

Тогда

Так как (интеграл Пуассона), то функция удовлетворяет дифференциальному уравнению

и начальному условию Решение этой задачи

Таким образом,

следовательно,

Полученная формула называется формулой Пуассона.

б) Пусть в точках х, стержня задано начальное распределение температур . Требуется найти температуру стержня в любой точке в момент времени при условии, что граничная точка либо поддерживается при ненулевой температуре, либо теплоизолирована. Это значит, что требуется найти решение дифференциального уравнения

при , ,

удовлетворяющее начальному условию

и одному из граничных условий

или

Чтобы решить эти задачи, рассмотрим решение задачи теплопроводности бесконечного стержня

где

Докажем следующее утверждение.

Лемма. Если функция нечетная, то решение удовлетворяет условию , если же функция четная, то удовлетворяет условию

В самом деле, если функция нечетная, то в силу нечетности подынтегральной функции. Если функция четная, то

так как функция четная.

Чтобы получить решения задач теплопроводности полубесконечного стержня, построим продолжение функции на всю числовую ось Ох нечетным или четным образом, то есть построим функции

если

если x<0;

если

если x<0;

_{Решение задачи теплопроводности для бесконечного стержня с начальным условием} удовлетворяет при

основному дифференциальному уравнению , начальному условию и граничному условию то есть функция рассматриваемая только при , является решением . Точно так же функция

рассматриваемая только при , является решением основного дифференциального уравнения, удовлетворяет начальному условию и граничному условию

Решения и можно преобразовать:

Если в первых интегралах сделать замену переменной то получим

или

,

.