3. Уравнения гиперболического типа с двумя независимыми переменными

3.1. Задача Коши

Рассмотрим уравнение

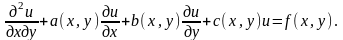
К такому виду приводится линейное гиперболическое уравнение с двумя независимыми переменными - непрерывные функции).

Уравнение характеристик для основного уравнения имеет вид

или

Эти уравнения имеют соответственно решения у и х. Следователь­но, x = const, у = const—суть характеристики уравнения.

Пусть в плоскости хОу дана дуга кривой l, которая пересе­кается не более чем в одной точке с прямыми, параллельными осям координат. Уравнение этой дуги может быть записано в виде y = g(x) или x = h(y). Будем считать, что существуют производные g' (х) и h' (х), отличные от нуля.

Пусть вдоль дуги кривой l заданы значения u и

Данные Коши позволяют на кривой y = g(x) найти значения производной Действительно, дифференцируя по x первое из условий, получим

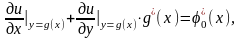
откуда

Задача Коши ставится так: требуется найти решения основного уравнения в некоторой окрестности кривой l, удовлетворяющее данным Коши .

Введем функции

Тогда наше уравнение равносильно системе трех уравнений

Рис. 3.1.

Возьмем в прямоугольнике ABCD (рис. 3.1) произвольную точку N (х> у) и прове­дем через нее характеристики NP и NQ до пересечения с кривой l. Интегрируя первое и третье уравнения системы по прямой QN, а второе—по PN, получим:

Очевидно, что если u(x_, у) есть решение нашего уравнения , удов­летворяющее данным Коши , то функции v, w и u удовлетво­ряют системе интегральных уравнений. Обратно, непрерывное решение (и, v, w) системы уравнений удовлетворяет, очевидно, системе дифференциальных уравнений, а функция u(х, у) удовлетворяет основному уравнению и условиям . Действительно, из третьего уравнения системы имеем

Кроме того,

Следовательно, оба уравнения выполняются. Легко видеть что u(х, у) удовлетворяет и данным Коши .

Таким образом, задача Коши свелась к доказательству существования непрерывного решения системы интегральных уравнений .

Решение системы будем искать методом последовательных приближений. За нулевое приближение берем

и следующие приближения вычисляются по формулам: и следующие приближения вычисляются по формулам:

Докажем равномерную сходимость последовательностей {v_n, w_n, u_n} в криволинейном треугольнике BCD (рис. 3.1).

Имеем:

Покажем, что разности (v_n-v_n-1), (w_n-w_n-1), (u_n-u_n-1) удовлетворяют неравенствам:

где При n=1 справедливость вышеприведенной системе очевидна, если выбрать А доста­точно большой. Покажем, что эти неравенства останутся справед­ливыми при замене n на n+1. Имеем

Точно так же оцениваются и другие и . Из оценок следует абсолютная и равномерная сходимость рядов

члены которых по абсолютной величине меньше членов равномерно сходящегося ряда

.

Следовательно, последовательные приближения v_n, w_n и u_n в кри­волинейном треугольнике BCD равномерно стремятся соответственно к определенным пределам v, w и u. Предельные функции непре­рывны, так как все последовательные приближения непрерывны. Переходя к пределу в формулах , мы получим, что предельные функции v{x_, у), w(x, у) и u(х, у) удовлетворяют системе .

Единственность решения системы . Допустим, что существуют два различных непрерывных решения системы v_l, w_1, u₁ и v_2, w_2, u₂. Обозначим V=v₁—v_2, W=w₁—w₂, U = u₁—u₂. Тогда V, W, U удовлетворяют однородной системе уравнений

Нужно доказать, что V = W = U = 0. Функции V, W и V не­прерывны и ограничены, как разности непрерывных функций в замкнутом криволинейном треугольнике BCD. Значит, суще­ствует такая постоянная В, что

Из (10) имеем:

Применив метод математической индукции, получим следующие оценки

для любого n. Отсюда следует, что V = W = U = 0, т. е. v_l = v₂, w_l=w_2, u₁ = u₂.