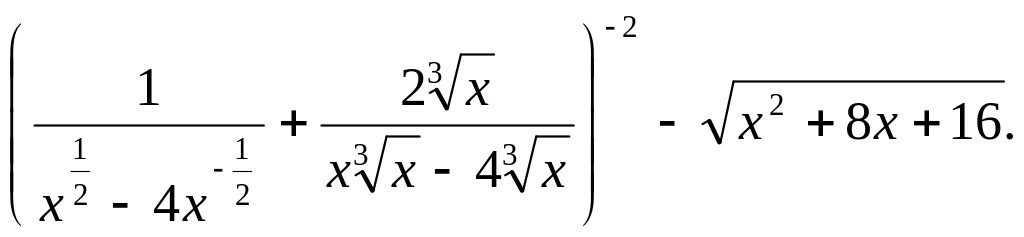2.4.3. Формулы сокращенного умножения

Для любых а и b верны равенства:

a²-b²=(a-b)(a+b);

(a+b)²=a²+2ab+b²;

(a-b)²=a²-2ab+b²;

(a+b)³=a³+3a²b+3ab²+b³;

(a-b)³ =a³-3a²b+3ab²-b³;

a³+b³=(a+b)(a²-ab+b²);

a³-b³=(a-b)(a²+ab+b²);

Пример 2.12. Разложить на множители (а+b+c)³-a³-b³-c³.

Представим выражение в виде ((а+b)+c)³-a³-b³-c³ и воспользуемся формулой куба суммы, получим (a+b)³+3(a+b)²c+3(a+b)c²+c³-(a³+b³)-c³=

(a+b)(a²+2ab+b²+3ac+3bc+3c²-a²+ab-b²), после приведения подобных членов (a+b)(3ab+3ac+3bc+3c²)=3(a+b)(a(b+c)+c(b+c))=3(a+b)(b+c)(a+c).

Ответ: 3(a+b)(b+c)(a+c).

Пример 2.13. Разложить на множители х⁴+4.

Представим х⁴+4=х⁴+4х²+4-4х²=(х²+2)²-(2х)²=(х²+2х+2)(х²-2х+2)

(использована формула а²+b²=(a+b)²-2ab).

2.4.4. Деление многочлена на многочлен

Стандартным видом многочлена Р(х) называется выражение

Р(х)=а₀хⁿ+a₁x^n-1+a₂x^n-2+…+a_n-1x+a_n,

где nN, a₀, a₁, …,a_n – действительные числа, причем а₀0.

Если существует многочлен S(x) такой, что Р(х)=Q(x)^/S(x), то говорят, что многочлен Р(х) делится на многочлен Q(x). Р(х) называется делимым, Q(x) – делителем, S(x) – частным.

Если многочлен Р(х) не делится на многочлен Q(x), то рассматривают деление с остатком, т.е. Р(х)=Q(x)^/S(x)+R(x), где степень многочлена R(x) меньше степени многочлена Q(x).

При делении многочленов, приведенных к стандартному виду, применяется правило «деления углом», аналогичное в некотором смысле правилу деления целых чисел.

Пример 2.14. Разделить многочлен на многочлен

(2х⁴-х³-6х²+7х-2): (х²+х-2)=2х²-3х+1.

2х⁴-х³-6х²+7х-2 х²+х-2

2х⁴+2х³-4х² 2х²-3х+1

-3х³-2х²+7х

-3х³-3х²+6х

х²+х-2

х²+х-2

0

Пример 2.15. Разделить многочлен на многочлен

х⁴-х³-6х²+10х-4 х³+5х²+4х-6

х⁴+5х³+4х²-6х х-6

-6х³-10х²+16х-4

-6х³-30х²-24х+36

20х²+40х-40

При тождественных преобразованиях алгебраических выражений применяются следующие приемы:

1) приведение алгебраических дробей к общему знаменателю;

2) разложение многочленов на множители;

а) с помощью формул сокращенного умножения;

б) с помощью их корней;

в) вынесением общего множителя за скобку;

г) способом группировки, а также их комбинации.

Тождественные преобразования алгебраических выражений

приведением алгебраических дробей к общему знаменателю

Пример 2.16. Упростить выражение

Будем последовательно приводить дроби к общему знаменателю

воспользуемся правилом деления дробей и снова приведем к общему знаменателю, получим

Ответ: 1/2.

Тождественные преобразования алгебраических выражений

на основании определения степени с отрицательным показателем

и с помощью формул сокращенного умножения

Пример 2.17. Упростить выражение

Воспользуемся определением степени с отрицательным показателем

(а>0), получим

Приведем к общему знаменателю числитель и знаменатель первой дроби и знаменатель второй

4х²+2х+1 – неполный квадрат суммы чисел 2х и 1, поэтому числитель разложим по формуле разности квадратов 1-64х⁶=(1-8х³)(1+8х³), а 4х²-4х+1=(1-2х)², затем разложим 1-8х³ как разность кубов, получим

Ответ: 1+2х.

Тождественные преобразования алгебраических выражений

разложением квадратного трехчлена на линейные множители

Пример 2.18. Упростить выражение х>1.

Воспользуемся формулой ax²+bx+c=a(x-x₁)(x-x₂), где х₁, х₂ – корни уравнения ах²+bx+c=0, разложим на множители квадратные трехчлены в числителе и знаменателе дроби:

Так как х>1, то в силу соотношения имеем Значит

откуда после сокращения получим Ответ:

Тождественные преобразования алгебраических выражений

методом группировки

Пример 2.19. Упростить выражение

Сгруппируем первое и второе слагаемые и третье и четвертое слагаемые, как в числителе, так и в знаменателе, получим

затем вынесем общие множители из каждой скобки

Из условия примера очевидно х>0, у>0, поэтому аналогично и в результате

Ответ:

Тождественные преобразования алгебраических выражений

делением многочлена на многочлен

Пример 2.20. Упростить выражение

Приведем каждую скобку к общему знаменателю, получим

• 17 –

разделим многочлен на многочлен

4х³-3х+1 2х²+х-1

4х³+2х²-2х 2х-1

-2х²-х+1

-2х²-х+1

0 Ответ: 2х-1.

Тождественные преобразования алгебраических выражений

освобождением от иррациональности знаменателей дробей

Пример 2.21. Упростить выражение

Избавимся от иррациональности в знаменателях первой и второй дроби, получим

Ответ:

Тождественные преобразования алгебраических выражений

приведением радикалов к одному показателю

Пример 2.22. Упростить выражение

Воспользуемся свойством приведем корни к одному показателю и предварительно вынесем общий множитель под вторым корнем

Ответ:

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ВАРИАНТ 1

1. 108, 216 и 135.

2. 

3. 

4. 

5. 

6. 

7. 

8. (ab+ac+bc)(a+b+c)-abc.

9. (x³+3x²+x-2): ( x+2).

10. 

11. 

12. 

13. 

ВАРИАНТ 2

1.360, 540 и 640.

2.

3.

4.

5.

6.

7.

8.а³+b³+c³-3abc.

9.(x⁴+2x³+2x²+2x+1) : (x+1).

10.

11.

12.

13.

ВАРИАНТ 3

1.680, 612.

2.

3.

4.

5.

6.

7.

8.х³+5х²+3х-9.

9.

10.

11.

12.

13.

ВАРИАНТ 4

1.195, 156 и 260.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13. х>а>0.

3. РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. УРАВНЕНИЯ,

СОДЕРЖАЩИЕ НЕИЗВЕСТНОЕ ПОД ЗНАКОМ МОДУЛЯ.

ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ

3.1.Рациональные уравнения

Рациональным называется уравнение, которое может быть приведено к виду Р(х)=0, где Р(х) – многочлен с действительными коэффициентами.

Основные методы решения рациональных уравнений

3 .1.1. Простейшие: решаются путем обычных упрощений – перенесения всех членов уравнения в одну часть, приведения к общему знаменателю, приведения подобных членов, в результате получается уравнение вида Р(х)/Q(х)=0, где Р(х) и Q(х) – многочлены первой или второй степени, решение которого сводится к решению системы Р(х)=0

Q(х)0