
917
.pdf
Пример 2.50. Даны векторы |
|
1; 3; 4 , |
|
3; |
4; 2 , |
̅ |
|
|||||||||||
1; 1; 4 . Найти пр с . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Предварительно найд м вектор |
|
с, учитывая, что при |
||||||||||||||||
сложении векторов их соответствующие координаты складывают: |
|
|
||||||||||||||||
с |
3 |
|
|
1 ; 4 1; 2 4 |
2; 3; 6 . |
|
|
|
|
|
|
|||||||
Искомую проекцию найд м по формуле: пр |
с |
|
|
с |
. |
|
|
|||||||||||
| |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
с| |
|
|
|||
Найд м модуль вектора |
|
с: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
2 |
|
3 |
6 |
|
7. |
|
|
|
|
|
|
|
|
||
Найд м скалярное произведение векторов |
и |
с: |
|
|
|
|
||||||||||||
|
с |
1 ∙ 2 |
|
|
3 ∙ 3 |
|
4 ∙ 6 35. |
|
|
|
|
|
|
|
||||
Тогда проекция вектора |
на ось вектора |
с: |
|
|
|
|
|
|
||||||||||
пр с |
|
|
с |
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| |
с| |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2.51. |
Даны точки |
|
2; 4; 7 , |
|
1; 1; 8 , |
|
5; 7; |
6 , |
||||||||||
7; 9; 9 . Найти пр |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Предварительно найд м координаты векторов |
и |
, |
||||||||||||||||
учитывая, что при нахождении координат вектора нужно из координат конца вектора вычесть координаты его начала:
1 |
2 ; 1 4; 8 7 |
|
1; 3; 1 , |
7 |
5 ; 9 7; 9 |
6 |
12; 16; 15 . |
Искомую проекцию найд м по формуле: пр
Найд м модуль вектора |
: |
|
|
|
||
| | |
|
|
|
|
|
|
12 |
16 |
15 |
|
25. |
|
|
Найд м скалярное произведение векторов |
и : |
|||||
∙ |
1 ∙ 12 |
3 ∙ |
16 |
1 ∙ 15 |
75. |
|
Тогда проекция вектора |
на ось вектора |
: |
||||
| ∙ | .
пр
Ответ: 3.
∙ |
|
3. |
| | |
|
|
|
||
|
|
2.14. Векторное произведение векторов
Векторным произведением вектора на вектор называется вектор ̅,
удовлетворяющий следующим условиям: |
|
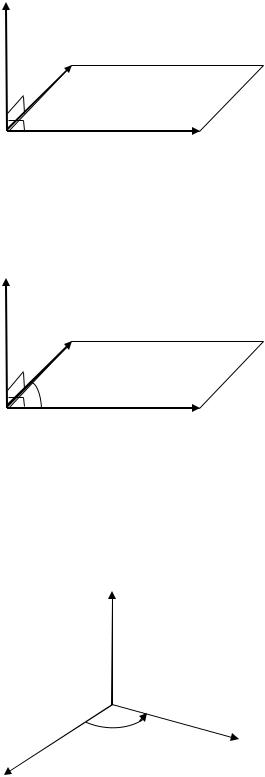
1. вектор ̅перпендикулярен векторам и , то есть ̅ , ̅ |
; это |
условие можно интерпретировать как перпендикулярность вектора |
̅плос- |
кости, в которой лежат векторы и (рис. 2.37); |
|
71
̅
Рис. 2.37. Перпендикулярность вектора ̅плоскости, в которой лежат векторы и
2. модуль вектора ̅равен площади параллелограмма, построенного на
векторах и как на сторонах, то есть | ̅| | | ∙ |
∙ sin , где – угол |
между векторами и (рис. 2.38); |
|
̅
Рис. 2.38. Площадь параллелограмма, построенного на векторах и
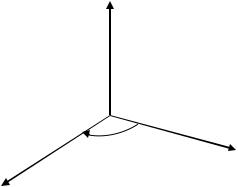
3. Векторы , , ̅образуют правую тройку векторов.
Три некомпланарных вектора , , ̅, взятые в указанном порядке, образуют правую тройку векторов, если с конца третьего вектора ̅кратчайший поворот от первого вектора ко второму вектору виден совершающимся против часовой стрелки (рис. 2.39), и левую, если виден совершающимся по часовой стрелке (рис. 2.40).
̅
Рис. 2.39. Векторы , , ̅образуют правую тройку векторов
|
Используется следующее обозначение векторного произведения век- |
|||
торов: |
или |
, . |
|
|
|
Пример 2.52. Векторы и образуют угол |
|
. Зная, что | | 6, |
|
|
|
|||
5, вычислить |
. |
|
|
|
|
|
72 |
|
|
̅
|
Рис. 2.40. Векторы |
, , ̅образуют левую тройку векторов |
|||||||||||||||||||||||
|
Решение. По определению векторного произведения |
|
|
|
|
||||||||||||||||||||
| |
| ∙ ∙ sin |
. Подставляя значения, получаем: |
6 ∙ 5 ∙ sin |
|
|
||||||||||||||||||||
|
|||||||||||||||||||||||||
15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 2.53. Найти скалярное произведение векторов |
и , зная, что |
|||||||||||||||||||||||
| | |
3, |
26, |
|
|
72. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Решение. По определению векторного произведения векторов: |
||||||||||||||||||||||||
|
|
|
|
| |
| ∙ |
∙ s |
|
, где |
– угол между векторами |
и . |
|||||||||||||||
|
Отсюда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
s |
| |
|
| |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
| |
|∙| |
| |
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
По определению скалярного произведения векторов: |
|
|
|
|
||||||||||||||||||||
|
| |
|
| ∙ |
|
∙ |
|
|
|
|
3 ∙ 26 ∙ |
|
|
30. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Ответ: |
|
|
30. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгебраические свойства векторного произведения векторов |
||||||||||||||||||||||||
|
1. |
|
|
|
|
|
|
. Свойство антиперестановочности сомножи- |
|||||||||||||||||
телей. Это свойство говорит о том, что при перестановке сомножителей векторное произведение меняет знак.
Доказательство. Векторы |
и |
коллинеарны, имеют одина- |
|||||
ковые модули, но противоположно направлены, так как тройки |
, |
, |
и |
||||
, , |
противоположной ориентации (рис. 2.41). Поэтому |
|
|
||||
|
. |
|
|
|
|
|
|
2. |
|
|
. Свойство сочетательности по |
||||
отношению к скалярному множителю. |
|
|
|
|
|||
Доказательство. Пусть |
0. Вектор |
перпендикулярен век- |
|||||
торам и |
. Вектор |
также перпендикулярен векторам |
и |
. Значит, |
|||
векторы |
и |
коллинеарны. Направления их совпадают. Они |
|||||
имеют одинаковые длины:
73
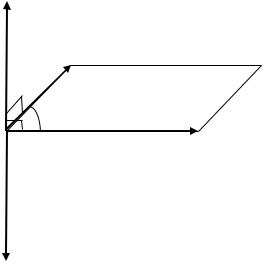
Рис. 2.41. Противоположная ориентация троек векторов |
, |
, |
и |
, , |
|||||||||
|
|
|
|
|
| |
| ∙ |
∙ |
, |
, |
|
|
|
|
|
|
|
| |
| ∙ |
∙ sin |
, |
| |
| ∙ |
∙ sin |
, . |
|
||
|
Поэтому |
|
|
|
. |
|
|
|
|
|
|
|
|
|
Доказательство проводится аналогично для |
|
0. |
|
|
||||||||
|
Аналогично доказывается равенство |
|
|
|
|
. |
|
||||||
|
3. |
|
с |
|
|
с. Свойство распределительности отно- |
|||||||
сительно сложения. Без доказательства. |
|
|
|
|
|
|
|
||||||
|
Пример 2.54. Раскрыть скобки и упростить выражение: |
|
|||||||||||
5 |
7 |
4 ̅ |
̅. |
|
|
|
|
|
|
|
|
|
|
|
Решение. |
5 |
7 |
4 ̅ |
̅ |
5 |
7 |
|
|
4 ̅ |
5 |
7 |
|
|
̅ |
4 ̅ 5 |
7 |
|
̅ |
5 |
7 |
|
|
4 ̅ 5 |
4 ̅ |
||
|
7 |
̅ |
5 |
|
̅ 7 |
20 |
̅ |
|
|
28 |
̅ |
|
|
5 ̅ |
7 ̅ |
20 |
|
̅ 28 |
̅ 5 |
|
|
̅ 7 |
̅. |
||||
Заметим, что векторное умножение векторных двучленов выполняется как в обычной алгебре за исключением свойства антиперестановочности сомножителей.
Ответ: 20 |
̅ |
28 |
̅ |
5 |
̅ 7 |
̅. |
Геометрические свойства векторного произведения векторов |
||||||
1. Если векторы |
|
и |
коллинеарны, то их векторное произведение |
|||
равно нулевому вектору. |
|
|
|
|
|
|
Доказательство. Если векторы |
и |
коллинеарны, то угол между |
||||
ними равен 0 или 180 . Рассмотрим модуль векторного произведения век-
торов и : |
| | ∙ ∙ sin , |
0. Модуль векторного произведе- |
|
ния равен нулю, а значит векторное произведение |
равно нулевому век- |
||
тору. |
|
|
|
Следствие. Векторное произведение вектора на этот же вектор равно
нулевому вектору: |
̅. |
|
74 |
|
Доказательство. |
Так как вектор |
коллинеарен самому себе, |
то по |
|||||||
свойству 1 его векторное произведение на себя равно нулевому вектору. |
|||||||||||
|
2. Если векторное произведение векторов и |
равно нулевому век- |
|||||||||
тору, то векторы |
и коллинеарны. |
|
|
|
|
|
|||||
|
Доказательство. Пусть |
|
̅. Тогда |
0 и | |
| ∙ |
∙ |
|
||||
∙ |
, |
0. Следовательно, |
угол между векторами |
и |
равен 0 |
или |
|||||
180 , а значит векторы |
и |
коллинеарны. |
|
|
|
|
|||||
|
3. Если векторы |
и приведены к общему началу, то модуль вектор- |
|||||||||
ного произведения векторов |
и |
равен площади параллелограмма, постро- |
|||||||||
енного на векторах |
и |
: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
парал. |
. |
|
|
|
|
|
Доказательство. Из элементарной геометрии известно, что площадь |
||||||||||
параллелограмма равна произведению его смежных сторон на синус угла
между ними: |
парал. |
| | ∙ |
∙ sin |
, . А это и есть модуль векторного |
||
произведения векторов |
и : |
парал. |
. |
|||
В частности, площадь треугольника, построенного на векторах и , |
||||||
привед нных к общему началу, находят по формуле: |
||||||
|
|
|
∆ |
|
|
. |
|
|
|
|
|||
Пример 2.55. Векторы |
и |
взаимно перпендикулярны. Зная, что |
||||
| | 3, |
4, найти |
3 |
|
2 . |
||
Решение. Применяя алгебраические и геометрические свойства векторного произведения, найд м векторное произведение векторных двучленов:
|
3 |
|
2 |
3 |
|
|
|
3 |
2 |
|
|
||
|
3 |
2 |
3 |
|
|
|
3 |
|
|
|
|
||
|
2 |
3 |
2 |
|
|
3 |
|
|
|
6 |
|
|
|
|
2 |
|
3 ̅ |
6 |
|
2 ̅ |
5 |
. |
|
|
|
||
|
Найд м модуль искомого векторного произведения: |
|
|||||||||||
|
3 |
|
2 |
5 |
|
|
5 |
5| | ∙ |
∙ |
||||
∙ |
, |
5 ∙ 3 ∙ 4 ∙ sin |
|
60. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Ответ: 60. |
|
|
|
|
|
|
|
|
|
|
||
|
Пример 2.56. Найти площадь параллелограмма, построенного на век- |
||||||||||||
торах |
3 ̅ |
2 и |
2 ̅ , где | |
̅| |
4, | |
| |
3, ̅, |
|
|
. |
|||
|
|||||||||||||
|
Решение. Воспользуемся формулой нахождения площади параллело- |
||||||||||||
грамма, построенного на векторах |
и |
: |
парал. |
. Найд м векторное |
|||||||||
произведение |
, используя алгебраические и геометрические свойства |
||||||||||||
векторного произведения. Получаем: |
|
|
|
|
|
|
|
||||||
|
|
|
3 ̅ 2 |
|
2 ̅ |
|
|
3 ̅ 2 |
2 ̅ |
|
|||
|
3 ̅ 2 |
|
2 ̅ 3 ̅ 2 |
|
|
|
3 ̅ 2 |
|
|||||
|
2 ̅ |
3 ̅ |
2 ̅ |
2 |
|
|
3 ̅ |
|
2 |
|
|
|
|
|
6 ̅ ̅ 4 ̅ |
3 |
̅ 2 |
|
|
6 ̅ 4 ̅ |
|
||||||
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
3 |
|
̅ |
|
|
2 ̅ |
7 |
̅ . |
|
|
|
|
|
|
|
||
|
|
Найд м модуль искомого векторного произведения: |
|
|||||||||||||
|
|
|
|
|
| 3 ̅ 2 |
2 ̅ |
|
| | 7 ̅ |
| 7| ̅ | |
|
||||||
|
| |
| |
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
∙ |
|
, |
|
7 ∙ 4 ∙ 3 ∙ sin |
|
42√2. |
|
|
|||||||
|
|
|
|
|||||||||||||
|
̅∙ |
|
|
|
|
|
|
|||||||||
|
|
Ответ: 42√2. |
|
|
|
|
|
|
|
|
||||||
|
|
Выражение векторного произведения векторов через коорди- |
||||||||||||||
наты перемножаемых векторов |
|
|
|
|
|
|
||||||||||
|
|
Векторы |
и |
заданы своими координатами: |
; ; |
и |
||||||||||
; |
; |
|
|
. Запишем разложение векторов |
|
и по ортам координатных |
||||||||||
осей: |
|
|
|
̅ |
|
|
̅ |
, |
̅ |
|
̅ |
. Используя определение век- |
||||
торного произведения, его алгебраические и геометрические свойства,
найд м векторное произведение векторов |
и : |
|
|||
|
̅ |
̅ |
̅ |
̅ |
|
̅ |
̅ |
̅ ̅ |
̅ |
̅ ̅ |
̅ ̅ |
̅ |
|
̅ |
|
̅ |
|
̅ |
|
̅ |
|
̅ |
̅ |
̅ |
̅ |
̅ |
|
̅ |
̅ |
|
|
|
|
|
̅ ̅ |
|
|
|
̅ |
̅ |
. |
Получили следующую формулу нахождения векторного произведения векторов через координаты перемножаемых векторов:
̅ ̅
.
Таким образом, векторное произведение векторов, заданных своими координатами, находят с помощью определителя третьего порядка, элементами первой строки которого являются орты координатных осей, элементами второй строки являются координаты первого вектора, элемен-
тами третьей строки являются координаты второго вектора. |
|
||||||||
Пример 2.57. Даны векторы |
|
5 ̅ 3 ̅ |
и |
2 ̅ 4 ̅ 7 . |
|||||
Найти их векторное произведение. |
|
|
|
|
|
|
|||
Решение. Векторы |
и заданы через разложение по ортам коорди- |
||||||||
натных осей. Запишем координаты векторов: |
5; 3; |
1 , |
|
||||||
2; 4; |
|
7 . Применяя формулу нахождения векторного произведения |
|||||||
векторов через координаты перемножаемых векторов, получаем: |
|
||||||||
|
|
̅ ̅ |
̅ |
̅ |
|
̅3 |
1 |
̅ 5 |
1 |
|
|
|
5 |
3 |
1 |
||||
|
|
|
2 |
4 |
7 |
4 |
7 |
2 |
7 |
|
|
|
|
|
|
|
|||
5 |
3 |
17 ̅ 37 ̅ 26 . |
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Ответ: 17 ̅ 37 ̅ 26 .
76

В условиях примера |
∆ |
|
| |
|
|. Найд м координаты векто- |
|||||||||||||||
|
|
|||||||||||||||||||
ров |
и |
, учитывая, что при нахождении координат вектора нужно из |
||||||||||||||||||
координат конца вектора вычесть координаты его начала: |
|
|
||||||||||||||||||
|
|
5 1; 6 |
|
1 ; 2 2 |
|
4; 5; 0 ; |
|
|
|
|
|
|||||||||
|
|
1 1; 3 |
1 ; 1 2 |
|
0; 4; 3 . |
|
|
|
|
|
||||||||||
Далее найд м векторное произведение векторов |
и |
: |
||||||||||||||||||
|
|
|
|
|
̅ |
̅ |
|
|
|
|
̅ |
̅ |
|
|
̅ 5 |
0 |
||||
|
|
|
|
|
|
|
4 |
|
5 |
0 |
|
|||||||||
|
|
|
|
|
|
|
0 |
|
4 |
3 |
|
4 |
|
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
̅4 0 |
4 |
5 |
|
15 ̅ 12 ̅ 16 . |
|
|
|
|
|
|
|
|||||||||
0 |
3 |
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда площадь треугольника: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
| |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∆ |
|
|
|
|
|
√15 |
|
12 |
16 |
|
|
√625 |
|
12,5. |
|||||
|
|
|
|
|
|
|
||||||||||||||
Ответ: 12,5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 2.61. Вектор ̅, перпендикулярный к оси |
|
и к вектору |
||||||||||||||||||
8; 15; 3 , образует острый угол с осью |
. Зная, что | ̅| |
51, найти его |
||||||||||||||||||
координаты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Так как по условию вектор |
̅перпендикулярен оси , то |
|||||||||||||||||||
вектор |
̅перпендикулярен орту оси |
|
, то есть вектору |
|
0; 0; 1 . Вектор |
|||||||||||||||
̅перпендикулярен также по условию вектору . Поэтому можно найти не-
который вектор |
, |
коллинеарный вектору |
̅, как векторное произведение |
||||||||||||
векторов |
и |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅ |
̅ |
̅ |
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
15 ̅ 8 .̅ |
|
|
|||
|
|
|
|
|
8 |
15 |
3 |
|
|
|
|
|
|
|
|
|
: | |
| |
|
|
|
|
|
||||||||
Далее найд м модуль вектора |
√15 |
8 |
|
17. По условию |
|||||||||||
| ̅| 51 и вектор |
̅образует острый угол с осью |
|
, поэтому |
̅ 3 |
|
||||||||||
45; 24; 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
45; 24; 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2.15. Смешанное произведение векторов |
|
|
|||||||||||
Смешанным произведением тр х векторов |
, |
, ̅называется скаляр- |
|||||||||||||
ное произведение векторного произведения векторов |
и |
на вектор |
̅: |
||||||||||||
∙ |
̅. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это произведение называют ещ |
векторно-скалярным произведением |
||||||||||||||
тр х векторов |
, |
, |
̅. |
|
|
|
|
|
|
|
|
|
|
|
|
Используется обозначение: |
̅. |
|
|
|
|
|
|
|
|
|
|||||
Пример 2.62. Вектор ̅перпендикулярен векторам |
и |
, угол между |
|||||||||||||
векторами |
и |
равен 30 . Зная, что | |
| |
6, |
|
|
3, | ̅| |
3, вычислить |
|||||||
̅. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Так как по условию вектор |
̅перпендикулярен векторам |
и |
|||||||||||||
, то вектор ̅коллинеарен некоторому вектору |
, равному векторному про- |
||||||||||||||
изведению векторов |
и |
: |
(рис. 2.43). |
|
|
|
|
|
|
||||||
|
|
|
|
|
78 |
|
|
|
|
|
|
|
|
|
|

̅
|
|
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.43. Вектор |
̅, коллинеарный вектору , равному векторному произведению |
|||||||||||||||
|
|
|
векторов и |
(к Примеру 2.62) |
|
|
|
|
|
|
|
|||||
В условии примера не указано, является тройка векторов |
, |
, |
̅левой |
|||||||||||||
или правой, поэтому угол между векторами |
и |
̅равен 0 |
или 180 . С уч - |
|||||||||||||
том сказанного находим смешанное произведение векторов |
, |
, |
̅: |
|
||||||||||||
̅ |
|
∙ |
̅ |
|
∙ | |
̅∙| cos 0 |
, |
|
|
|
|
∙ | |
̅∙| |
1, |
||
|
∙ | |
̅∙| cos 180 |
|
|
|
∙ | |
̅| ∙ |
1 |
||||||||
|
|
|
|
|
|
|
||||||||||
∙ | |
̅|, |
| |
| ∙ |
∙ sin 30 |
∙ | |
̅,| |
6 ∙ 3 ∙ |
|
|
∙ 3, |
27. |
|
|
|||
|
|
|
||||||||||||||
∙ | |
̅| |
| |
| ∙ |
∙ sin 30 |
∙ | ̅| |
6 ∙ 3 ∙ |
|
|
∙ 3 |
|
|
|||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||
Ответ: |
27. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геометрические свойства смешанного произведения векторов |
||||||||||||||||
1. Смешанное произведение векторов |
, |
, ̅– это число, абсолютная |
||||||||||||||
величина которого равна объ му параллелепипеда, построенного на векто-
рах , , ̅как на р брах: парал. |
̅. |
|
Доказательство. Построим параллелепипед, р брами которого явля- |
||
ются векторы , , ̅. Построим вектор |
̅ |
(рис. 2.44). |
̅
̅
Рис. 2.44. Объ м параллелепипеда, построенного на векторах , , ̅
Рассмотрим смешанное произведение векторов , , ̅:
79
