
917
.pdf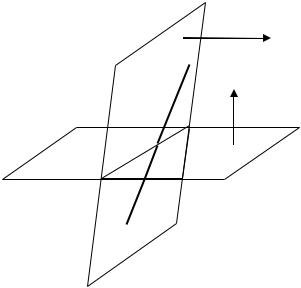
Пример 4.17. Составить уравнения проекции прямой 5 |
4 |
2 |
|||
5 0 и |
2 |
2 0 на плоскость 2 |
1 0. |
|
|
Решение. Проекцией данной прямой на данную плоскость является прямая. Эта прямая образуется при пересечении проектирующей плоскости с данной плоскостью. Исходная прямая задана как пересечение двух плоскостей. Поэтому проектирующая плоскость проходит через прямую пересечения этих плоскостей перпендикулярно заданной плоскости.
Обозначим:
–исходная прямая;
–плоскость, на которую прямая проектируется;
–проектирующая плоскость;
– нормальный вектор плоскости |
; |
– нормальный вектор плоскости |
(рис. 4.4). |
|
Рис. 4.4. Составление проекции прямой |
на плоскость |
|
||||||
Для составления уравнения проектирующей плоскости |
воспользу- |
||||||||
емся уравнением пучка плоскостей. Получаем: |
|
|
|||||||
5 |
4 |
2 |
5 |
|
2 |
2 |
0. |
|
|
Преобразуем к общему уравнению плоскости: |
|
||||||||
5 |
|
4 |
|
2 |
2 |
5 |
2 |
0. |
|
Запишем координаты нормального вектора плоскости |
: |
||||||||
|
5 |
; |
4; |
2 |
2 . |
|
|
|
|
Запишем координаты нормального вектора плоскости |
: |
||||||||
|
2; |
1; 1 . |
|
|
|
|
|
|
|
Так как плоскости |
и перпендикулярны, то их нормальные векторы |
||||||||
итакже перпендикулярны. Если векторы перпендикулярны, то их скалярное произведение равно нулю. Найд м скалярное произведение векторов
ичерез координаты векторов:
∙ |
5 |
∙ 2 |
4 ∙ 1 |
2 2 ∙ 1 4 |
12. |
Приравниваем полученное выражение к нулю:
4 12 0.
160
Отсюда |
|
3. |
|
|
|
|
Подставляем значение |
3 в уравнение пучка плоскостей, приве- |
|||||
д нного к общему уравнению: |
|
|
|
|||
5 3 |
4 |
2 2 ∙ 3 |
5 2 ∙ 3 |
0. |
||
Преобразуем: |
|
|
|
|
||
2 |
4 |
8 |
1 0. |
|
|
|
Получили уравнение проектирующей плоскости .
Искомые уравнения проекции запишем в виде системы уравнений
проектирующей плоскости |
и данной плоскости : |
||||||
2 |
4 |
|
8 |
1 |
0, |
|
|
|
2 |
|
|
1 |
0. |
|
|
Ответ: |
2 |
|
4 |
8 |
1 |
0, |
|
2 |
|
|
|
1 |
0. |
||
4.5. Переход от уравнения прямой, заданной как пересечение двух плоскостей, к каноническим уравнениям прямой
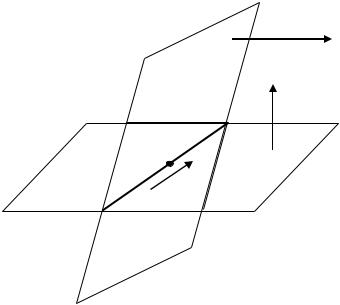
Пусть прямая задана как пересечение двух плоскостей (рис. 4.5):
0,
0.
Рис. 4.5. Переход от уравнения прямой, заданной как пересечение плоскостей, к каноническим уравнениям прямой
Для составления канонических уравнений прямой необходимо выполнить следующие действия.
1. Найти точку ; ; прямой. Прямая задана как пересечение двух плоскостей. Поэтому любая точка прямой принадлежит одновременно обоим плоскостям. Для нахождения точки прямой нужно задать численное значение одной из координат, подставить его в каждое уравнение системы.
161
В результате получим систему из двух уравнений с двумя неизвестными. Решив систему, найд м значения остальных координат.
2. Найти направляющий вектор |
; ; |
прямой, учитывая, что он |
|
перпендикулярен нормальным векторам |
; |
; |
и |
;; плоскостей, определяющих прямую. Такой вектор можно
найти как векторное произведение нормальных векторов: |
|
. |
||
Пример 4.18. Составить канонические уравнения прямой, заданной |
||||
как пересечение двух плоскостей 5 |
0 и 2 |
3 |
2 |
5 0. |
Решение. Для составления канонических уравнений прямой нужно знать точку прямой и направляющий вектор прямой. Прямая задана как пересечение двух плоскостей. Поэтому любая точка прямой принадлежит одновременно обоим плоскостям. Зададим численное значение, например, 0, и подставим в каждое уравнение плоскости. Получаем систему уравнений:
|
|
0, |
|
|
|
3 |
2 |
5 |
0. |
|
|
|
Решаем полученную систему. Сложим уравнения, предварительно |
||||
умножив первое уравнение на 2. Получаем: 5 |
5 0. Отсюда |
1. |
|||
Подставив |
|
1 в первое уравнение, найд м |
1. Получаем точку пря- |
||
мой: |
0; |
|
1; 1 . |
|
|
|
Далее находим направляющий вектор прямой как векторное произве- |
||||
дение нормальных векторов плоскостей. Нормальный вектор первой плоско-
сти: |
|
|
|
5; 1; 1 , нормальный вектор второй плоскости: |
||||||||||||||||||||||||||||||||
2; 3; |
|
|
|
2 . Находим направляющий вектор прямой: |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅ |
|
̅ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
5 |
|
|
1 |
|
|
|
|
1 |
|
|
5 ̅ 12 ̅ 13 . |
|
|
|||||||||||||||||||||
|
|
2 |
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
5; 12; 13 . |
||||||||||||||||||
Таким, образом, направляющий вектор прямой: |
|
|
|
|||||||||||||||||||||||||||||||||
|
Составляем канонические уравнения прямой: |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.6. Угол между двумя прямыми |
|
|
||||||||||||||||||
|
Пусть две прямые |
|
|
|
и |
заданы каноническими уравнениями: |
||||||||||||||||||||||||||||||
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Угол между двумя прямыми определяется как угол между их направ- |
|||||||||||||||||||||||||||||||||||
ляющими векторами |
; |
; |
|
|
и |
; ; |
. Получаем: |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|∙| |
| |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
162

Полученная формула позволяет находить угол между двумя прямыми через координаты их направляющих векторов.
При нахождении острого угла между прямыми значение косинуса берут положительным. В этом случае формула нахождения угла принимает вид:
|
| |
∙ | |
|
|
|
| |
|
|
| |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
| |
|∙| |
| |
|
|
|
|
|
|
||||||||
|
|
∙ |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Эта формула позволяет находить острый угол между двумя пря- |
||||||||||||||||
мыми через координаты их направляющих векторов. |
|
|
|
|
|
|
|
|
||||||||
Пример 4.19. Найти острый угол между прямыми |
|
|
|
|
|
|
и |
|||||||||
|
|
|
|
|||||||||||||
.
Решение. Для нахождения угла между двумя прямыми нужно знать координаты их направляющих векторов и . Прямые заданы каноническими уравнениями. Поэтому координаты направляющих векторов находятся в знаменателях дробей. Находим направляющие векторы прямых:
11; 8; 7 , |
7; |
2; 8 . Находим косинус острого угла между направляю- |
|||||||||||||||||||||||||||
щими векторами прямой: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
cos |
| |
|
|
|
|
|
|
| |
|
|
|
| ∙ ∙ |
∙ | |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
√ |
|
∙ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
√ . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
√ ∙√ |
|
|
|
√ |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Отсюда |
|
|
. |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 , |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Пример 4.20. Найти острый угол между прямыми |
3 |
4 , и |
||||||||||||||||||||||||
7 |
|
10 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
11 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Решение. Для нахождения угла между двумя прямыми нужно знать |
||||||||||||||||||||||||||
координаты их направляющих векторов и |
. Прямые заданы параметри- |
||||||||||||||||||||||||||||
ческими уравнениями. Поэтому координаты направляющих векторов – это числовые множители перед параметром . Находим направляющие векторы
прямых: |
2; 4; 4 , |
|
|
10; 11; 2 . Находим косинус острого угла |
|||||||||||||||||||||
между направляющими векторами прямой: |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
cos |
| |
|
|
|
|
| |
|
|
|
|
| ∙ |
∙ |
∙ |
| |
|
| | |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|||||
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
∙√ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
. Отсюда |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 0, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Пример 4.21. Найти острый угол между прямыми |
||||||||||||||||||||||
3 |
|
4 |
|
|
7 0 и 5 |
3 |
1 0, 2 |
2 |
|
|
4 0. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
163 |
|
|
|
|
|
|
|
|
|
|
|||

Решение. Для нахождения угла между двумя прямыми нужно знать координаты их направляющих векторов и . Прямые заданы как пересечение плоскостей. Поэтому координаты направляющих векторов – это векторные произведения нормальных векторов плоскостей. Обозначим нор-
мальные векторы, определяющие первую прямую, через |
, и , |
. Обозна- |
|||||
чим нормальные векторы, определяющие вторую прямую, через |
, и , . |
||||||
Находим направляющий вектор первой прямой: |
|
|
|||||
|
|
̅ |
̅ |
|
|
|
|
, |
, |
1 |
2 |
0 |
2 ̅ ̅ 2 . |
|
|
|
|
3 |
4 |
1 |
|
2; |
1; 2 . |
Таким, образом, направляющий вектор первой прямой: |
|||||||
Находим направляющий вектор второй прямой:
|
|
|
̅ |
̅ |
|
|
|
|
|
|
|
|
|
|
, |
|
, |
5 |
3 |
1 |
|
̅ 3 ̅ 4 . |
|
|
|
|
|
||
|
|
|
2 |
2 |
1 |
|
|
|
|
|
1; |
3; 4 . |
||
Таким, образом, направляющий вектор второй прямой: |
|
|
||||||||||||
Находим косинус острого угла между направляющими векторами пря- |
||||||||||||||
мой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
| |
|
|
| |
|
|
|
| ∙ |
|
∙ |
∙ |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
∙ |
|
| | |
√ |
∙√ √ √
Ответ: √
. Отсюда |
√ |
|
. |
|
.
|
|
|
|
4.7. Угол между прямой и плоскостью |
||
|
Пусть прямая задана каноническими уравнениями: |
|||||
|
|
|
|
|
|
. |
|
|
|
|
|
||
и плоскость |
задана общим уравнением: |
|||||
|
|
|
0. |
|||
Угол |
между прямой и плоскостью можно определить следующим |
|||||
образом. Сначала найти угол между данной прямой и прямой, перпендикулярной плоскости. Этот угол определяется как угол между направляющим
вектором |
данной прямой и нормальным вектором данной плоскости. За- |
|||
тем угол |
между данной прямой и данной плоскостью можно определить |
|||
по формуле: |
|
|
(рис. 4.6). |
|
|
||||
Находим угол |
: |
|||
cos
∙ |
|
|
. |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
| |∙| | √ |
∙√ |
||||||
|
|||||||
Находим искомый угол : |
|
|
|
|
|
|||
sin |
sin |
|
cos |
|
|
|
|
. |
|
|
|
|
|
||||
|
√ |
∙√ |
||||||
|
|
|
|
|
||||
164


|
|
|
4.8. Взаимное расположение двух прямых |
|||||
Пусть две прямые |
|
и заданы каноническими уравнениями: |
||||||
|
: |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|||
|
: |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||
Данные прямые параллельны, если их направляющие векторы |
||||||||
; ; |
|
и |
; ; |
|
коллинеарны (рис. 4.7). |
|||
Рис. 4.7. Две параллельные прямые
Векторы коллинеарны, если их соответствующие координаты пропорциональны. Получаем:
.
Полученное равенство является условием параллельности двух пря-
мых.
Данные прямые перпендикулярны, если их направляющие векторы ; ; и ; ; перпендикулярны (рис. 4.8).
Рис. 4.8. Две перпендикулярны прямые
166

Если векторы перпендикулярны, то их скалярное произведение равно нулю, то есть сумма произведений соответствующих координат векторов равна нулю. Получаем:
.
Полученное равенство является условием перпендикулярности двух прямых.
Пример 4.23. Выяснить, параллельны ли прямые:
1) |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) |
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
; |
|
5 |
|
2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
3 |
|
|
|
2 |
0, |
||||||||||||
3) |
2 |
, |
и |
|
|
|
|||||||||||||||
3 |
2 |
0. |
|||||||||||||||||||
7 .
Решение. Прямые параллельны, если координаты их направляющих векторов пропорциональны.
1) Прямые заданы каноническими уравнениями. Поэтому координаты их направляющих векторов находятся в знаменателях дробей. Запишем направляющие векторы прямых:
3; 4; 2 , 6; 8; 4 .
Составляем пропорции из координат векторов:
.
Равенства верные, поэтому прямые параллельны.
2) Прямые заданы каноническими уравнениями. Поэтому координаты их направляющих векторов находятся в знаменателях дробей. Запишем направляющие векторы прямых:
2; 3; 5 , 4; 6; 5 .
Составляем пропорции из координат векторов:
.
Равенства неверные, поэтому прямые не параллельны.
3) Первая прямая задана параметрическими уравнениями. Поэтому координаты е направляющего вектора – это числовые множителями перед параметром . Запишем направляющий вектор первой прямой:
2; 1; 1 .
Вторая прямая задана как пересечение плоскостей. Поэтому е направляющий вектор можно найти как векторное произведение нормальных векторов плоскостей. Запишем направляющий вектор второй прямой:
̅̅
1 |
3 |
1 |
8 ̅ 4 ̅ 4 . Таким образом, направляющий вектор вто- |
1 |
1 |
3 |
8; 4; 4 . |
рой прямой: |
|||
Составляем пропорции из координат векторов:
.
Равенства верные, поэтому прямые параллельны.
167
Ответ: 1) прямые параллельны; 2) прямые не параллельны; 3) прямые параллельны.
Пример 4.24. Выяснить, перпендикулярны ли прямые:
|
5 |
|
2 |
, |
|
|
|
2 |
3 |
, |
|
|
|||
1) |
1 |
|
6 |
, и |
|
4 |
4 |
, |
|
|
|||||
|
3 |
|
9 . |
|
|
|
7 |
2 . |
|
|
|||||
|
|
|
|
4 |
|
|
3 , |
|
|
3 |
|
6 , |
|
|
|
2) |
|
|
|
|
7 , и |
|
5 |
|
2 , |
|
|
||||
3) |
2 |
2 . |
|
и |
12 |
|
3 . |
6 |
0, |
||||||
|
|
|
|
|
|
|
|
|
3 |
|
4 |
3 |
0. |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Прямые перпендикулярны, если сумма произведений соответствующих координат их направляющих векторов равна нулю.
1) Прямые заданы параметрическими уравнениями. Поэтому координаты их направляющих векторов – это числовые множителями перед параметром . Запишем направляющие векторы прямых:
2; |
6; 9 , |
3; 4; |
2 . |
Находим сумму произведений соответствующих координат направля- |
|||
ющих векторов: |
|
|
|
2 ∙ 3 |
6 ∙ 4 |
9 ∙ 2 |
0. |
Поэтому прямые перпендикулярны.
2) Прямые заданы параметрическими уравнениями. Поэтому координаты их направляющих векторов – это числовые множители перед параметром . Запишем направляющие векторы прямых:
3; 7; |
2 , |
6; 2; 3 . |
|
Находим сумму произведений соответствующих координат направля- |
|||
ющих векторов: |
|
|
|
3 ∙ 6 |
7 ∙ 2 |
2 ∙ 3 |
10 0. |
Поэтому прямые не перпендикулярны.
3) Первая прямая задана каноническими уравнениями. Поэтому координаты е направляющего вектора находятся в знаменателях дробей. Запи-
шем направляющий вектор первой прямой: |
1; 3; 5 . |
Вторая прямая задана как пересечение плоскостей. Поэтому е направляющий вектор можно найти как векторное произведение нормальных векторов плоскостей. Запишем направляющий вектор второй прямой:
̅̅
1 |
2 |
1 |
9 ̅ ̅ 7 . Таким образом, направляющий вектор второй |
3 |
1 |
4 |
9; 1; 7 . |
прямой: |
|
||
|
Находим сумму произведений соответствующих координат направля- |
||
ющих векторов: |
|||
|
|
1 ∙ 9 |
3 ∙ 1 5 ∙ 7 23 0. |
Поэтому прямые не перпендикулярны.
Ответ: 1) прямые перпендикулярны; 2) прямые не перпендикулярны; 3) прямые не перпендикулярны.
168

