
917
.pdf
|
; |
; |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Таким образом, при вычитании двух векторов их соответствующие |
|||||||||||||||||||||
координаты вычитают. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Пример 2.14. Заданы два векторы |
|
5; |
3; 1 |
и |
6; |
4; 7 . |
|||||||||||||||
Найти координаты следующих векторов: 1) |
; 2) |
; 3) |
3 ; 4) |
|
; |
|||||||||||||||||
|
||||||||||||||||||||||
5) 4 |
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1) Учитывая, что при сложении векторов их соответствующие коорди- |
|||||||||||||||||||||
наты складывают, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
5 6; |
3 |
|
|
4 ; |
1 |
7 |
|
11; |
7; 6 ; |
|
|
|
|||||||
|
2) Учитывая, что при вычитании векторов их соответствующие коор- |
|||||||||||||||||||||
динаты вычитают, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
5 6; 3 |
|
|
4 ; 1 7 |
|
1; 1; 8 ; |
|
|
|
|||||||||||
|
3) Учитывая, что при умножении вектора на число каждая координата |
|||||||||||||||||||||
вектора умножается на это число, получаем: |
|
|
|
|
|
|
||||||||||||||||
|
3 |
|
3 ∙ 5; |
3 ∙ |
3 ; |
3 ∙ |
1 |
|
15; 9; 3 ; |
|
|
|
||||||||||
|
4) Учитывая, что при умножении вектора на число каждая координата |
|||||||||||||||||||||
вектора умножается на это число, получаем: |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
∙ 6; |
|
∙ |
4 ; |
|
∙ 7 |
|
|
|
; |
|
; 1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
5) Найд м сначала координаты векторов 4 |
и 3 , |
учитывая, что при |
|||||||||||||||||||
умножении вектора на число каждая координата вектора умножается на это число:
4 |
4 ∙ 5; 4 ∙ |
3 ; 4 ∙ |
1 |
20; 12; |
4 , |
|
|
|
|
|
|
|
|||||
3 |
3 ∙ 6; 3 ∙ |
4 ; 3 ∙ 7 |
|
18; |
12; 21 . |
|
|
|
|
|
|
|
|
||||
Далее найд м координаты искомого вектора, учитывая, что при вычи- |
|||||||||||||||||
тании векторов их соответствующие координаты вычитают: |
|
|
|
|
|
|
|
||||||||||
4 |
3 |
20 |
18; 12 |
|
12 ; |
4 |
21 |
2; 0; |
25 . |
|
|
|
|
||||
Ответ: 1) |
11; |
7; 6 ; 2) |
1; 1; |
8 ; 3) |
15; 9; 3 ; 4) |
|
|
; |
|
|
; 1 |
; |
|||||
|
|
||||||||||||||||
5) 2; 0; |
25 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2.15. Даны точки |
6; 4; 1 , |
5; 3; 9 , |
|
2; 7; |
4 , |
||||||||||||
3; 2; |
8 . Найти координаты вектора |
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. |
Предварительно найд м координаты векторов |
|
|
и |
, |
||||||||||||
учитывая, что при нахождении координат вектора нужно из координат конца вычесть координаты его начала:
5 |
|
6 ; 3 |
|
4 ; 9 1 |
|
1; 7; 10 , |
||||
3 |
2; |
2 |
7; |
8 |
4 |
|
|
1; |
9; |
4 . |
Далее найд м координаты вектора |
|
|
, учитывая, что при умножении |
|||||||
|
||||||||||
вектора на число каждая координата вектора умножается на это число:
∙ 1; |
|
∙ 9 ; |
|
4 |
|
; 3; |
|
. |
|
|
|
|
Найд м координаты искомого вектора, учитывая, что при сложении векторов их соответствующие координаты складывают:
50

1 |
|
; 7 |
3 ; 10 |
|
|
|
; 4; |
|
. |
|
|
|
|
Ответ: |
|
; 4; |
|
. |
|
|
2.9.Условие коллинеарности двух векторов
вкоординатной форме
Даны векторы: |
; ; |
и |
; |
; |
. Если векторы |
и |
коллинеарны, то вектор |
может быть получен из вектора растяжением |
|||||
его в определ нное число раз. Иначе, вектор |
может быть получен из век- |
|||||
тора умножением его на действительное число |
. Можно записать: |
, |
||||
где – действительное число. Так как при умножении вектора на число каж-
дая координата вектора умножается на это число, то |
, |
, |
||||||
. Отсюда: |
|
|
||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
Полученное равенство является условием коллинеарности векторов. Таким образом, если векторы коллинеарны, то их соответствующие
координаты пропорциональны. Верно и обратное. |
|
|
|
Пример 2.16. Определить, коллинеарны ли векторы |
4; 6; 2 |
и |
2; 3; 1 . |
|
|
Решение. Векторы коллинеарны, если их соответствующие коорди- |
|
наты пропорциональны. Составим пропорции из соответствующих коорди- |
|
|||||||||
нат векторов: |
|
|
|
|
|
. Равенства верные, следовательно векторы кол- |
|
|||
|
|
|
|
|||||||
линеарны. |
|
|
|
|
|
|
|
|
|
|
Ответ: векторы коллинеарны. |
|
|
|
|
||||||
Пример 2.17. Даны точки |
2; 8; 3 , |
1; 5; 4 , 2; 0; 7 , |
|
|||||||
9; 6; 2 . Определить, коллинеарны ли векторы |
и . |
|
|
|||||||
Решение. |
Предварительно найд м координаты векторов |
и |
, |
|||||||
учитывая, что при нахождении координат вектора нужно из координат конца вектора вычесть координаты его начала:
1 |
|
2 ; 5 |
8 |
; |
4 |
3 |
1; 13; 7 , |
|
9 |
2; |
6 |
0; 2 |
7 |
|
7; |
6; |
5 . |
Векторы коллинеарны, если их соответствующие координаты пропорциональны. Составим пропорции из соответствующих координат векторов
и: . Равенства неверные, следовательно векторы не колли-
неарны.
Ответ: векторы не коллинеарны.
Пример 2.18. Определить, при каких значениях и векторы 2; 3; и ; 6; 2 коллинеарны.
Решение. Векторы коллинеарны, если их соответствующие координаты пропорциональны. Составим пропорции из соответствующих коорди-
нат векторов |
и : |
|
|
|
|
|
|
. Отсюда можно записать равенства: |
|||||
|
|
|
|
||||||||||
|
|
, |
4 и |
|
|
|
, |
1. |
|
||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
51 |
|||
Ответ: |
4, |
1. |
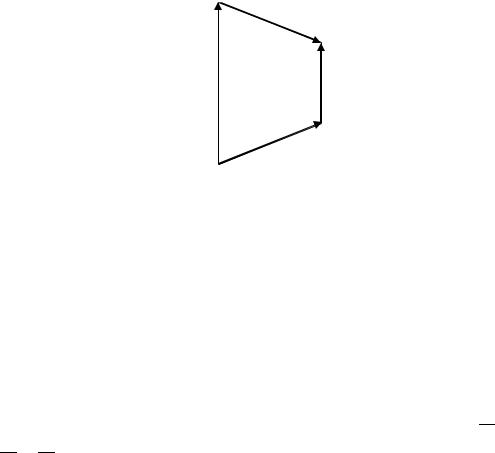
Пример 2.19. Проверить, что четыре точки 3; 1; 2 , 1; 2; 1 , 1; 1; 3 , 3; 5; 3 служат вершинами трапеции.
Решение. Выполним схематичный черт ж (рис. 2.30). Трапецией называется четыр хугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Покажем этот факт для данного четыр х- угольника. Для этого найд м координаты векторов, совпадающих со сторонами трапеции, то есть координаты векторов , , , . При нахождении координат вектора нужно из координат конца вектора вычесть координаты его начала. Получаем:
Рис. 2.30. Доказательство того, что четыр хугольник |
– трапеция |
|||||||
|
|
|
(к Примеру 2.19) |
|
|
|
||
1 3; 2 |
1 ; 1 2 |
2; 3; 3 , |
|
|
||||
1 |
1; 1 |
2; |
3 |
1 |
2; |
1; |
2 , |
|
1 |
3; 1 |
|
5 ; 3 3 |
4; 6; 6 , |
|
|||
3 3; 5 |
|
1 ; 3 2 |
0; 4; 1 . |
|
|
|||
|
Заметим, что векторы |
и |
коллинеарны, поскольку их соответ- |
||||||
ствующие координаты пропорциональны: |
|
|
|
|
|
. Значит стороны |
|||
|
|
|
|
||||||
и |
четыр хугольника параллельны. Векторы |
|
и |
не коллинеарны, |
|||||
поскольку их соответствующие координаты не пропорциональны:
. Значит стороны |
и |
четыр хугольника не параллельны. |
Таким образом, в данном четыр хугольнике две стороны параллельны, а две другие стороны не параллельны. Следовательно, четыр х- угольник является трапецией.
2.10. Нахождение модуля вектора через его координаты
Рассмотрим вектор |
; ; |
и совместим его с началом коор- |
|
динат. Конец вектора обозначим точкой |
. Провед м через точку |
плос- |
|
кости, перпендикулярные |
координатным |
осям. Точки пересечения |
этих |
плоскостей с осями координат обозначим , , . Провед нные плоскости вместе с координатными плоскостями образуют прямоугольный парал-
лелепипед, диагональю которого служит вектор |
(рис. 2.31). |
52 |
|

Рис. 2.31. Модуль вектора
Из элементарной геометрии известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин его смежных сторон. Поэтому:
|
|
. |
|
|
|
|
|
Но |
| |, |
, |
, |
. Из предыдущего равен- |
|||
ства получаем: |
|
|
|
|
|
|
|
| | |
|
или | |
| |
|
|
|
|
|
|
. |
|||||
Таким образом: |
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
. |
|
||
Полученная формула означает, что модуль вектора равен квадрат-
ному корню из суммы квадратов соответствующих координат вектора.
|
Пример 2.20. Вычислить модуль вектора |
5; |
1; |
|
3 . |
|||||||||
|
Решение. Для вычисления модуля вектора применяем формулу: | | |
|||||||||||||
|
|
|
|
. В условиях примера |
5, |
1, |
|
|
3. Подстав- |
|||||
|
|
|
|
|
|
|||||||||
ляем: |
|
|
|
|
|
|
|
|
||||||
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
3 |
|
√35. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ответ: √35. |
|
|
|
|
|
|
|
|
|||||
|
Пример 2.21. Даны точки |
5; |
1; 2 и |
3; |
|
2; 6 . Найти модуль |
||||||||
вектора . |
|
|
|
|
|
|
|
|
||||||
|
Решение. Предварительно найд м координаты вектора |
, учитывая, |
||||||||||||
что при нахождении координат вектора нужно из координат конца вектора вычесть координаты его начала:
|
3 |
|
5 ; 2 |
|
1 ; 6 2 |
2; 1; 4 . |
|
|
|||
Найд м модуль вектора |
: |
|
|
|
|
|
|||||
| | |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
4 |
√21. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: √21. |
|
|
|
|
|
|
|
|
|||
Пример 2.22. Даны две координаты вектора : |
4, |
12. |
|||||||||
Определить его третью координату при условии, что | | |
13. |
|
|||||||||
53

|
|
|
|
Решение. Воспользуемся формулой нахождения |
модуля |
вектора: |
|||||||||||||||||||||||||||||||||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4, |
12, |
| | |
13. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
В условиях примера |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляем: 13 |
|
|
4 |
|
|
12 |
|
. Отсюда |
|
3. |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
Ответ: |
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Пример 2.23. Найти орт вектора |
|
|
6; |
|
2; |
3 . |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
Решение. Для нахождения орта вектора используем формулу |
|
||||||||||||||||||||||||||||||||||
|
|
|
. Запишем иначе: |
|
|
|
|
|
|
|
|
|
|
. Эту формулу можно трактовать следующим |
|||||||||||||||||||||||||
|
| | |
|
|
|
| | |
||||||||||||||||||||||||||||||||||
образом: орт вектора – это вектор, полученный из вектора |
умножением его |
||||||||||||||||||||||||||||||||||||||
на число |
|
. Учитывая, что при умножении вектора на число каждая коор- |
|||||||||||||||||||||||||||||||||||||
| | |
|||||||||||||||||||||||||||||||||||||||
дината вектора умножается на это число, каждую координату вектора |
надо |
||||||||||||||||||||||||||||||||||||||
умножить на число |
|
|
|
|
|
|
или разделить на число | |. Находим | |: |
|
|
||||||||||||||||||||||||||||||
| |
| |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
2 |
|
|
3 |
|
7. |
Тогда орт вектора : |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
; |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Ответ: |
|
; |
|
|
|
|
; |
|
|
|
|
|
|
. |
|
|
|
|
|
7; 3; |
6 , |
|
5; 2; |
3 , |
4; 8; 4 , |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
Пример 2.24. Даны точки |
|
||||||||||||||||||||||||||||||||||
|
10; 11; |
|
|
5 . Проверить, что векторы |
и |
коллинеарны; установить, |
|||||||||||||||||||||||||||||||||
какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.
Решение. Предварительно найд м координаты векторов и , учитывая, что при нахождении координат вектора нужно из координат конца вектора вычесть координаты его начала:
5 |
7 ; 2 3; 3 |
6 |
2; 1; 3 , |
10 |
4 ; 11 8; 5 |
4 |
6; 3; 9 . |
Векторы коллинеарны, если их соответствующие координаты пропорциональны. Составим пропорции из соответствующих координат векторов
и: . Равенства верные, следовательно векторы коллине-
арны.
Установим, какой из векторов длиннее и во сколько раз. Для этого найд м модули векторов:
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
3 |
|
|
√14, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6 |
3 |
|
9 |
|
|
√126 |
3√14. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
|
|
|
|
|
|
|
|
Видно, что вектор |
длиннее вектора |
. Так как |
|
√ |
|
3, то |
||||||||||||||||||||
| |
| |
|
|
|
|
|
||||||||||||||||||||
√ |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вектор |
длиннее вектора |
в 3 раза. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Далее выясним, как направлены векторы |
и |
– в одну или в про- |
||||||||||||||||||||||||
тивоположные стороны. Заметим, что |
3 ∙ |
|
, то есть векторы |
и |
||||||||||||||||||||||
направлены в противоположные стороны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ответ: вектор |
|
длиннее вектора |
в 3 раза; векторы |
и |
||||||||||||||||||||||
направлены в противоположные стороны.
54
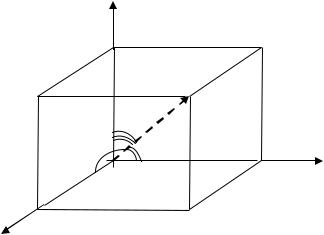
2.11. Направляющие косинусы вектора |
|
||
Рассмотрим вектор |
; ; |
и совместим его с началом коор- |
|
динат. Конец вектора обозначим точкой |
. Провед м через точку |
плос- |
|
кости, перпендикулярные |
координатным |
осям. Точки пересечения |
этих |
плоскостей с осями координат обозначим , , . Провед нные плоскости вместе с координатными плоскостями образуют прямоугольный парал-
лелепипед, диагональю которого служит вектор |
. |
||
Угол, который образует вектор с осью |
обозначим через , с осью |
||
обозначим через |
, с осью |
обозначим через (рис. 2.32). Косинусы |
|
этих углов: cos , cos |
, cos |
называются направляющими косинусами век- |
|
тора . |
|
|
|
Рис. 2.32. Углы, образуемые вектором с осями координат
Выразим координаты вектора через его модуль и направляющие косинусы, учитывая, что координатами вектора называются проекции вектора на оси координат, и учитывая формулу нахождения проекции вектора на ось через его модуль и направляющие косинусы:
|
|
|
|
пр |
| |
| ∙ cos , |
|
|
пр |
| |
|
| ∙ cos , |
|
|
|
пр |
|||||
| |
|
| ∙ cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Из этих равенств получаем формулы нахождения направляющих ко- |
|||||||||||||||||
синусов вектора через координаты вектора и его модуль: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
, |
|
|
|
, |
|
|
|
. |
|
||||
|
|
|
|
|
|
| | |
| | |
| | |
|||||||||||||
|
|
|
|
Возводя в квадрат левую и правую части каждого из равенств и сум- |
|||||||||||||||||
мируя полученные выражения, получаем: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
cos |
cos |
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
| | |
| | |
| | |
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
| |
| |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
|
|
|
|
При помощи этой формулы можно вычислить любой из углов , , , |
|||||||||||||||||
зная два других. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
|
|
|
|
|||
Если выразить модуль вектора |
через его координаты, |
то формулы |
||||||||||||||||
нахождения направляющих косинусов вектора принимают вид: |
|
|
|
|||||||||||||||
|
|
|
|
|
, |
|
|
|
|
, |
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
Направляющие косинусы вектора связаны с ортом вектора. Учитывая |
||||||||||||||||||
формулу нахождения |
орта вектора : |
|
|
|
|
и формулы |
нахождения |
|||||||||||
| | |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
направляющих косинусов вектора , получаем, что координатами орта век-
тора являются его направляющие косинусы: |
|
cos |
|
; cos ; cos . |
||||||||||||||||||||||||||||||||||||||||
Пример 2.25. Вычислить направляющие косинусы вектора |
|
|||||||||||||||||||||||||||||||||||||||||||
6; |
5; 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Вычислим модуль вектора |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
5 |
|
2 |
|
|
|
|
√65. |
|
||||||||
Тогда направляющие косинусы вектора : |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
, |
cos |
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
√ |
, |
|||||||||
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
√ |
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
√ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
| | √ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: cos |
|
|
|
|
|
|
|
|
√ |
|
, |
|
cos |
|
|
√ |
, cos |
|
√ |
. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Пример 2.26. Может ли вектор составлять с координатными осями |
||||||||||||||||||||||||||||||||||||||||||||
углы |
90 , |
|
|
|
|
150 , |
|
|
60 ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. Косинусы углов |
, |
, являются направляющими косину- |
||||||||||||||||||||||||||||||||||||||||||
сами вектора. Воспользуемся формулой, связывающей направляющие коси-
нусы вектора: cos |
|
cos |
cos |
1. Подставляем данные примера в |
||||
эту формулу: |
|
|
|
|
|
|||
cos |
90 cos |
150 |
cos 60 |
1. |
||||
Получаем: |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
√ |
|
|
|
1, |
|
||
|
|
|
|
|
|
|
||
1 |
1. |
|
|
|
|
|
|
|
Равенство верное, поэтому вектор может составлять с координатными осями указанные углы.
Ответ: может.
Пример 2.27. Может ли вектор составлять с двумя координатными
осями углы |
30 , |
45 ? |
Решение. Косинусы углов , являются направляющими косинусами вектора. Воспользуемся формулой, связывающей направляющие косинусы вектора: cos cos cos 1. Здесь – угол, составляемый вектором с третьей координатной осью. Подставляем данные примера в эту формулу:
cos 30 |
cos 45 |
|
|
cos |
|
1. |
|||
|
|
|
|
|
|
|
|
|
|
Получаем: |
√ |
√ |
cos |
1. |
|||||
Отсюда cos |
|
|
, что является противоречивым равенством, по- |
||||||
|
|
||||||||
скольку квадрат числа на множестве действительных чисел не может быть отрицательным.
56

Ответ: не может. |
|
|
|
|
Пример 2.28. Вектор составляет с осями |
и |
углы |
120 , |
|
45 . Какой угол он составляет с осью |
? |
|
|
|
Решение. Косинусы углов , |
являются направляющими косинусами |
|||
вектора. Воспользуемся формулой, связывающей направляющие косинусы
вектора: cos |
|
cos |
|
cos |
1. Здесь |
– угол, составляемый векто- |
|||||||||||||||||||||||
ром с осью . Подставляем данные примера в эту формулу: |
|
|
|
||||||||||||||||||||||||||
cos |
120 |
|
|
cos |
|
|
cos 45 |
1. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получаем: |
|
|
|
|
|
|
|
|
cos |
√ |
1. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Отсюда cos |
|
|
|
|
|
, cos |
|
|
|
, |
60 |
|
или |
|
120 . |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Ответ: 60 |
|
или 120 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 2.29. Вектор |
|
составляет с осью |
угол 60 , а с осью |
− |
|||||||||||||||||||||||||
угол 45 . Длина вектора |
|
|
равна 8. Найти координаты вектора |
, если его |
|||||||||||||||||||||||||
первая координата отрицательна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Решение. Воспользуемся формулами нахождения направляющих ко- |
|||||||||||||||||||||||||||||
синусов вектора для углов, которые составляет вектор |
с осями |
|
и |
: |
|||||||||||||||||||||||||
cos |
|
|
|
, cos |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
| | |
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Выразим отсюда координаты |
|
|
|
|
и |
: |
|
|
|
|
|
|
|
|
|||||||||||||||
|
| | cos |
, |
|
|
|
| |
|
| cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
По условию | |
| 8, |
60 , |
|
|
|
|
|
45 . |
|
|
|
|
|
|
|
|
|||||||||||||
Подставляем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
8 cos 60 |
4, |
|
|
8 cos 45 |
|
4√2. |
|
|
|
|
|
|||||||||||||||||
Далее найд м cos |
|
из формулы cos |
|
cos |
|
cos |
1. Так как |
||||||||||||||||||||||
по условию первая координата вектора |
отрицательна, то cos |
|
0. Полу- |
||||||||||||||||||||||||||
чаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
cos |
|
|
|
1 |
|
|
cos |
|
|
|
cos |
|
|
|
|
|
√1 |
cos |
60 |
cos 45 |
|
|
|
||||||
1 |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем воспользуемся формулой нахождения направляющего косинуса |
|||||||||||||||||||
вектора для угла, который составляет вектор |
с осью : cos |
|
|
. Выра- |
|||||||||||||||
|
| | |
||||||||||||||||||
зим отсюда координату : |
| | cos . Учитывая, что | | |
8, cos |
|
||||||||||||||||
|
|||||||||||||||||||
, получаем: |
8 ∙ |
|
|
4. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
Запишем координаты вектора : |
4; 4; 4√2 . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: |
|
|
4; 4; 4√2 . |
|
|
|
|
|
|
|
|
||||||||
2.12. Разложение вектора по ортам координатных осей
Рассмотрим тройку векторов ,̅ ,̅ . Эти векторы определяются следующими условиями:
1) вектор ̅лежит на оси Ox, вектор ̅лежит на оси Oy, вектор лежит на оси Oz;
57

2) каждый из векторов ,̅,̅ направлен на своей оси в положительную
сторону; |
|
3) векторы ,̅ ,̅ – единичные, то есть | |̅ | |̅ |
1 (рис. 2.33). |
̅
̅
Рис. 2.33. Орты координатных осей
Векторы ,̅ ,̅ называют ортами координатных осей.
Рассмотрим произвольный вектор |
и совместим его с началом коор- |
динат. Конец вектора обозначим точкой |
. Провед м через точку плос- |
кости, перпендикулярные координатным осям. Точки пересечения этих плоскостей с осями координат обозначим , , . Провед нные плоскости вместе с координатными плоскостями образуют прямоугольный парал-
лелепипед, диагональю которого служит вектор |
(рис. 2.34). |
̅̅
Рис. 2.34. Разложение вектора по ортам координатных осей
По правилу сложения векторов: |
|
|
|
|
. |
|
|
Так как векторы |
и ̅коллинеарны, то вектор |
может быть по- |
|
лучен растяжением вектора |
̅в определ нное число раз, то есть |
,̅где |
|
|
58 |
|
|
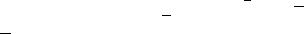
– некоторое положительное число. Аналогично, |
|
,̅ |
, где |
|||||||||
, – некоторые положительные числа. Таким образом, |
̅ |
̅ |
||||||||||
, то есть любой вектор в пространстве может быть выражен через век- |
||||||||||||
торы ,̅ ,̅ |
при помощи линейных операций. |
|
|
|
|
|||||||
|
Выясним геометрический смысл коэффициентов |
, , . |
|
|||||||||
|
Рассмотрим модуль вектора |
: |
|
|
|
|
|
|||||
|
| |
| |
| |̅ |
| |̅ |
∙ 1 |
. |
|
|
|
|
|
|
|
С другой стороны, | |
| |
пр |
|
. Следовательно, |
, то есть |
||||||
коэффициент |
равен первой координате вектора . |
|
|
|
||||||||
|
Аналогично: |
|
|
|
|
|
|
|
|
|
||
|
|
|
| |̅ |
| |̅ |
∙ 1 |
|
и |
|
пр |
|
. |
|
|
Следовательно, |
|
, то есть коэффициент |
равен второй коорди- |
||||||||
нате координате вектора . |
|
|
|
|
|
|
|
|
||||
|
Аналогично: |
|
|
|
|
|
|
|
|
|
||
|
| |
| |
|
|
∙ 1 |
|
и | |
| |
пр |
|
. |
|
|
Следовательно, |
|
, то есть коэффициент |
равен третьей коорди- |
||||||||
нате вектора |
, |
|
|
|
|
|
|
|
|
|
||
|
Таким образом, вектор можно представить следующим образом: |
|||||||||||
|
|
|
|
|
|
|
̅ |
̅ |
, |
|
|
|
где |
, |
, |
– координаты вектора |
, векторы |
,̅ ,̅ |
– орты координатных |
||||||
осей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Эту формулу называют разложением вектора по ортам координат- |
|||||||||||
ных осей. Кратко записывают |
|
; ; |
. |
|
|
|
|
|||||
|
Пример 2.30. Записать разложение вектора |
|
6; 4; 9 |
по ортам |
||||||||
координатных осей. |
|
|
|
|
|
|
|
|
|
|||
|
Решение. Воспользуемся формулой разложения вектора по ортам ко- |
|||||||||||
ординатных осей: |
̅ |
̅ |
|
. По условию заданы координаты век- |
||||||||
тора |
: |
|
6, |
4, |
9. Подставляем: |
|
6 ̅ 4 ̅ 9 . |
|||||
|
Ответ: |
6 ̅ 4 ̅ 9 . |
|
|
|
|
|
|
|
|||
|
|
|
2.13. Скалярное произведение векторов |
|
||||||||
|
Скалярным произведением вектора |
на вектор |
называется число, |
|||||||||
равное произведению модулей этих векторов на косинус угла между ними:
|
|
|
|
| | ∙ |
∙ |
, |
|
где |
– угол между векторами |
и . |
|
|
|
||
|
Обозначение: |
, ∙ , |
, . |
|
|
|
|
|
Пример 2.31. |
Найти скалярное произведение векторов и , если |
|||||
| | |
5, |
2, угол между векторами |
|
. |
|
||
|
|
||||||
Решение. Используем формулу нахождения скалярного произведения двух векторов через их модули и косинус угла между ними:
| | ∙ ∙ cos 5 ∙ 2 ∙ cos 5 ∙ 2 ∙ √ 5√3.
Ответ: 5√3.
59
