
917
.pdf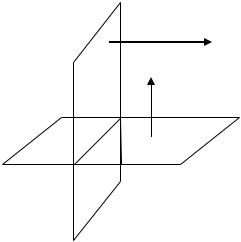
|
|
Решаем систему. Сложив уравнения, получаем: |
|
|
|
|
|
|
|
|
2. Отсюда |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
3. Подставляем это значение во второе уравнение системы: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1. Отсюда |
|
|
|
|
|
|
|
. |
|
|
3 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Подставляем значения |
|
в уравнение |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
Пример 3.12. Составить уравнение плоскости, перпендикулярной |
||||||||||||||||||||||||||||||||||
плоскости 2 |
2 |
4 |
|
|
|
|
|
5 0 и отсекающей на координатных осях |
|
и |
|||||||||||||||||||||||||||
|
|
отрезки |
|
|
2 и |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение. Обозначим искомую плоскость через , обозначим данную плоскость через , обозначим нормальный вектор искомой плоскости через
, обозначим нормальный вектор данной плоскости через
(рис. 3.19).
|
|
|
Рис. 3.19. Две перпендикулярные плоскости (к Примеру 3.12) |
|||||||||||||||||
|
|
Воспользуемся уравнением плоскости в отрезках: |
|
|||||||||||||||||
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
, |
|
и – это величины отрезков, которые плоскость отсекает на осях |
|||||||||||||||||
координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
По условию |
|
2 и |
|
|
. Подставляем: |
|
|
|
|
|
|
|
1. Преобра- |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
зуем полученное уравнение к общему уравнению плоскости. |
|
|||||||||||||||||||
|
|
Умножим уравнение на |
2 : |
|
|
|
|
|
|
|
|
|||||||||
|
|
3 |
2 |
2 |
0. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Запишем координаты нормального вектора искомой плоскости: |
||||||||||||||||||
; |
3 |
; 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Запишем координаты нормального вектора данной плоскости по е |
||||||||||||||||||
общему уравнению: |
|
2; |
2; 4 . |
|
|
|
|
|
|
|
|
|||||||||
|
|
Так как плоскости |
и |
|
перпендикулярны, то их нормальные век- |
|||||||||||||||
торы |
|
и тоже перпендикулярны. Если векторы перпендикулярны, то их |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
||
скалярное произведение равно нулю. Используя формулу скалярного произведения векторов через координаты этих векторов, получаем:
∙ ∙ 2 3 ∙ 2 2 ∙ 4 8 8.
Приравниваем скалярное произведение векторов к нулю:
8 8 0.
Отсюда |
1. |
|
|
|
|
|
|
|
|
|
Подставляя значение |
1 в уравнение |
3 |
2 |
2 |
0, по- |
|||||
лучим уравнение искомой плоскости: |
|
|
|
|
|
|
||||
1 ∙ |
3 ∙ 1 ∙ |
2 |
2 ∙ 1 0. |
|
|
|
|
|
|
|
Преобразуем: |
|
|
|
|
|
|
|
|
||
3 |
2 |
2 |
0. |
|
|
|
|
|
|
|
Ответ: |
3 |
2 |
2 0. |
|
|
|
|
|
|
|
3.4. Уравнение плоскости, проходящей через три данные точки |
||||||||||
Пусть |
|
; ; |
, |
; ; |
, |
; ; |
|
– заданные точки од- |
||
ной плоскости и |
; |
; |
– произвольная точка этой же плоскости. Рас- |
|||||||
смотрим три вектора: |
, |
, |
|
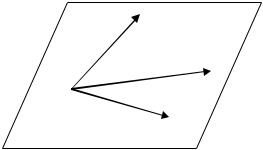
(рис. 3.20). |
|
|
|
|
||
Рис. 3.20. Плоскость, проходящая через три данные точки
Найд м координаты этих векторов:
; |
; |
, |
; |
; |
, |
; |
; |
. |
Эти векторы лежат в одной плоскости, то есть они компланарны и поэтому их смешанное произведение равно нулю:
0.
Используя формулу смешанного произведения векторов в координатной форме, получаем:
.
Полученное уравнение называется уравнением плоскости, проходя-
щей через три данные точки.
На практике полученный определитель удобно раскрывать разложением по первой строке. После преобразований уравнение приводится к общему уравнению плоскости.
121
|
Пример 3.13. Составить уравнение плоскости, проходящей через |
||||||
точки |
|
4; 2; |
5 , |
1; |
3; 2 , |
|
6; 0; 7 . |
|
Решение. Воспользуемся уравнением плоскости, проходящей через |
||||||
три данные точки: |
|
|
|
|
|||
|
|
|
|
|
|
0, |
|
где |
, , |
– координаты одной точки плоскости, , , – координаты |
|||||
другой точки плоскости и , |
, – координаты третьей точки плоскости, |
||||||
, , |
– координаты произвольной точки плоскости. Подставляем числовые |
||||||
данные: |
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
5 |
|
|
1 |
4 |
3 |
2 |
2 |
5 |
0. |
|
6 |
4 |
0 |
2 |
7 |
5 |
|
|
Преобразуем: |
|
|
|
|
||
|
|
4 |
2 |
5 |
|
|
|
|
3 |
|
5 |
7 |
0. |
|
|
|
10 |
|
2 |
2 |
|
|
|
|
Раскрывая определитель разложением по первой строке, получаем: |
||||||
|
24 |
4 |
76 |
2 |
44 |
5 |
0. |
|
Преобразуем: |
|
|
|
|
||
|
6 |
4 |
19 |
2 |
11 |
5 |
0, |
|
6 |
19 |
11 |
41 |
0. |
|
|
|
Ответ: 6 |
19 |
11 |
41 |
0. |
|
|
|
|
3.4. Нормальное уравнение плоскости |
|
|
|
|||
|
|
Рассмотрим плоскость . Опустим перпендикуляр из начала коорди- |
||||||
нат на эту плоскость. Получим точку . Рассмотрим орт вектора |
: |
|
||||||
|
. Обозначим вектор |
через , обозначим модуль вектора |
через . |
|||||
| | |
||||||||
Тогда |
| | . Пусть |
; ; – произвольная точка плоскости (рис. 3.21). |
||||||
Заметим, что вектор является нормальным вектором плоскости. |
|
|
||||||
|
|
Известно, что орт любого вектора имеет своими координатами |
||||||
направляющие косинусы этого вектора. Поэтому: |
cos |
; cos |
; cos |
, |
||||
где |
, |
, – углы, которые составляет вектор |
с осями |
, , |
соот- |
|||
ветственно. |
|
|
|
|
|
|
||
|
|
Далее найд м проекцию вектора |
на направление вектора , |
ис- |
||||
пользуя формулу нахождения угла между векторами через скалярное произведение векторов и модули векторов, а также, учитывая, что модуль орта равен 1:
пр |
| | cos |
| |
| |
∙ |
∙ |
∙ |
, |
|
|
|
|
||||||
| |∙| | |
|
|||||||
где – угол между векторами |
и |
|
. |
|
|
|
|
|
122

где cos , cos , cos – направляющие косинусы нормального вектора плоскости, – расстояние от начала координат до плоскости. Поэтому можно записать два условия: 1) 0; 2) cos cos cos 1. Первое условие говорит о том, что числовое слагаемое в уравнении должно быть отрицательным. Второе условие говорит о том, что сумма квадратов перед квадратами переменных равна 1.
Для каждого из данных уравнений будем проверять эти условия. Если оба условия выполняются, то уравнение является нормальным. Если одно из условий или оба условия не выполняются, то уравнение не является нормаль-
ным. |
|
|
|
||||
1) Проверяем первое условие: 5 |
0. Первое условие выполняется. |
||||||
Проверяем второе условие: |
|
|
|
|
|
|
1. Второе условие вы- |
|
|
|
|||||
полняется. Так как оба условия выполняются, то уравнение является нормальным.
2) |
Проверяем первое условие: 5 0. Первое условие не выполняется, |
|||||||||||||
поэтому уравнение не является нормальным. |
||||||||||||||
3) |
Проверяем первое условие: |
1 |
0. Первое условие выполняется. |
|||||||||||
Проверяем второе условие: |
|
|
|
|
|
|
|
|
|
|
|
|
1. Второе условие |
|
|
|
|
|
|
||||||||||
не выполняются, поэтому уравнение не является нормальным. |
||||||||||||||
4) |
Проверяем первое условие: |
1 |
0. Первое условие выполняется. |
|||||||||||
Проверяем второе условие: 0 |
|
|
|
|
|
|
|
|
1. Второе условие выпол- |
|||||
|
|
|
|
|
|
|
||||||||
няется. Так как оба условия выполняются, то уравнение является нормальным.
|
|
|
|
5) Проверяем первое условие: 2 0. Первое условие не выполняется, |
|||||||||||||||||||||||||||||||||||||||||||||
поэтому уравнение не является нормальным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
Ответ: 1), 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
Пример 3.15. Привести каждое из следующих уравнений к нормаль- |
|||||||||||||||||||||||||||||||||||||||||||||
ному виду: 1) 11 |
10 |
2 |
5 |
0; 2) |
|
|
|
|
|
|
|
|
|
3 0; 3) 5 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
12 26 0; 4) 2 |
|
|
1 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Решение. Все плоскости заданы общим уравнением. Для приведения |
|||||||||||||||||||||||||||||||||||||||||||||
общего уравнения плоскости |
|
|
|
|
|
|
|
|
|
0 к нормальному уравне- |
|||||||||||||||||||||||||||||||||||||||
нию, надо общее уравнение умножить на нормирующий множитель |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
, где знак |
выбирается противоположным знаку коэффициента |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
√ |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1) Вычисляем нормирующий множитель: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Умножая исходное |
|
уравнение |
на |
нормирующий |
множитель, |
получаем: |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. Преобразуем: |
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|
|
|
1. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2) Вычисляем нормирующий множитель: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Умножая исходное уравнение на нормирующий |
множитель, |
получаем: |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
0. |
|
|
124 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
3) Вычисляем нормирующий множитель: |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Умножая исходное уравнение на нормирующий |
множитель, |
|
получаем: |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0. Преобразуем: |
|
|
|
|
2 |
0. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
4) Вычисляем нормирующий множитель: |
|
|
|
|
|
|
|
|
. Умножая |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
√ |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
исходное уравнение на нормирующий множитель, получаем: |
|
|
|
|
0. |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
Ответ: 1) |
|
|
|
|
|
|
|
|
|
|
|
0; 2) |
|
|
|
|
|
|
|
|
|
3 |
|
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3) |
|
|
|
|
|
2 |
0; 4) |
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Пример 3.16. Для каждой из следующих плоскостей вычислить углы |
|||||||||||||||||||||||||||||||||||||||||
, , |
|
, образуемые нормальным вектором с осями координат, и расстояние |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
от начала координат до плоскости: 1) |
|
|
√2 |
16 0; 2) 2 |
|
3 |
|
|
||||||||||||||||||||||||||||||||||||
6 |
|
4 0; 3) |
|
|
2 0; 4) |
2 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Решение. Воспользуемся нормальным уравнением плоскости: |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
cos |
cos |
0, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
где cos , cos , cos |
– направляющие косинусы нормального вектора плос- |
|||||||||||||||||||||||||||||||||||||||||||
кости, поэтому , |
, , – углы, образуемые нормальным вектором с осями |
|||||||||||||||||||||||||||||||||||||||||||
координат; – расстояние от начала координат до плоскости. Для нахождения требуемых величин надо заданное уравнение плоскости привести к нормальному уравнению.
1) Вычисляем нормирующий множитель:
√
. Умножая исходное уравнение на нормирующий множитель, полу-
чаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
8 0. Отсюда: cos |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
120 ; |
cos |
|
|
|
|
|
|
|
|
, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
60 ; cos |
|
|
|
|
|
|
|
|
√ , |
|
|
|
|
|
45 ; |
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
2) Вычисляем нормирующий множитель: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Умножая исходное уравнение на нормирующий |
множитель, |
получаем: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. Отсюда: cos |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; cos |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; cos |
|
|
|
|
|
, |
|
|
|
|
|
; |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
3) Вычисляем нормирующий множитель: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
√ |
|
. Умножая исходное уравнение на нормирующий множитель, полу- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
√ |
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
чаем: |
|
|
|
|
|
|
√2 0. Отсюда: cos |
0, |
|
|
|
|
|
90 ; cos |
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
√ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
135 ; cos |
|
|
|
45 ; |
√2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
4) Вычисляем нормирующий множитель: |
|
|
|
|
|
|
|
|
|
|
|
|
|
1, то есть |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
√ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
плоскость задана нормальным уравнением. Отсюда: cos |
0, |
|
|
90 ; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
cos |
0, |
|
|
|
|
|
90 ; cos |
1, |
0 ; |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
Ответ: 1) |
120 , |
60 , |
45 , |
8; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
; |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
3) |
90 |
, |
135 , |
45 , |
√2; |
||
4) |
90 |
, |
90 , |
0 , |
2. |
|
|
|
3.5. Угол между двумя плоскостями |
||||||
Пусть плоскости |
|
и заданы общим уравнением: |
|||||
|
|
|
|
0 и |
0 |
||
соответственно. Угол между плоскостями определяется как угол между их нормальными векторами. Запишем нормальные векторы плоскостей:
; ; , |
; ; . |
|
|
Далее воспользуемся формулой угла между векторами через скаляр- |
|||
ное произведение этих векторов и их модули. Получаем: |
|||
|
|
∙ |
|
|
|
, |
|
|
| |∙| | |
||
где – угол между векторами и .
Используя формулу скалярного произведения векторов в координатной форме и формулу для нахождения модуля вектора через его координаты, получаем следующую формулу, позволяющую находить угол между двумя плоскостями по заданным общим уравнениям плоскостей:
|
|
|
|
|
. |
|
|
|
|
||
|
|
||||
|
|
|
∙ |
||
Полученная формула позволяет находить угол между двумя плоскостями по заданным общим уравнениям плоскостей.
Пример 3.17. Определить двугранный угол, образованный пересече-
нием следующих пар плоскостей: |
|
|
|
|
|
|||||
1) 3 |
|
0, 2 |
0; |
|
|
|
|
|
|
|
2) 3 |
4 |
12 |
7 0, 8 |
6 |
11 0. |
|
||||
Решение. Для нахождения двугранного угла между плоскостями вос- |
||||||||||
пользуемся формулой: |
|
|
|
|
|
|
|
|
||
|
|
|
cos |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
∙ |
|||
где , , |
– координаты нормального вектора одной плоскости, , , |
|||||||||
– координаты нормального вектора другой плоскости.
Обе плоскости заданы общим уравнением. В качестве координат нормального вектора каждой плоскости можно взять коэффициенты перед пере-
менными в общем уравнении плоскости. |
|
|
1) Запишем нормальные векторы: |
0; 3; 1 , |
0; 2; 1 . |
Вычисляем угол: cos
|
∙ ∙ |
|
∙ |
|
|
|
|
|
√ |
|
. Отсюда |
|
|
|
|
|
|
|
|
|
|
||
|
|
∙√ |
|
√ ∙√ |
|||||||
|
|
|
|
|
|||||||
|
|
. |
|
|
|
|
|
|
|
3; |
4; 12 , |
8; 0; 6 . |
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
2) Запишем нормальные векторы: |
|||||||||||||||
|
|
Вычисляем угол: cos |
|
∙ |
∙ |
∙ |
|
|
|
|
. От- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∙ |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сюда |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Ответ: 1) |
|
|
; 2) |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
126 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Пример 3.18. Вычислить угол между плоскостями, проходящими че-
рез точку 1; 1; 1 , одна из которых содержит ось |
, а другая – ось . |
|||
Решение. Обозначим плоскость, проходящую через ось |
через . |
|||
Обозначим плоскость, проходящую через ось |
через |
. Обозначим нор- |
||
мальные векторы этих плоскостей через и |
соответственно. |
|
||
Так как плоскость |
проходит через ось |
, то е |
уравнение можно |
|
записать в виде |
0. Так как плоскость |
проходит через ось , то |
||
е уравнение можно записать в виде |
0. Так как обе плоскости |
|||
проходят через точку , то координаты этой точки удовлетворяют уравнениям обеих плоскостей.
|
Подставляем координаты точки |
в уравнение плоскости |
|
: ∙ |
|||||||||
1 |
∙ |
1 |
0. Отсюда |
|
. Подставляем полученное выражение |
||||||||
в уравнение плоскости : |
|
|
|
0. Отсюда |
0. Запишем нор- |
||||||||
мальный вектор плоскости |
: |
|
0; 1; |
1 . |
|
|
|
||||||
|
Подставляем координаты точки |
в уравнение плоскости |
: |
∙ 1 |
|||||||||
∙ |
1 |
0. Отсюда |
. Подставляем полученное выражение в уравне- |
||||||||||
ние плоскости |
: |
0. |
Отсюда |
|
|
0. Запишем нормальный |
|||||||
вектор плоскости |
: |
1; 1; 0 . |
|
|
|
|
|
|
|||||
|
Найд м угол между плоскостями по формуле: |
|
|
|
|||||||||
|
|
|
cos |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
∙ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
где |
, , |
– координаты нормального вектора одной плоскости, |
, |
, |
|||||||||
– координаты нормального вектора другой плоскости. |
|
|
|
||||||||||
Вычисляем угол: cos
Ответ: 60 .
|
∙ ∙ |
|
|
∙ |
|
|
. Отсюда |
60 . |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
∙√ |
|
|||||
|
|
|
|
|
|
|
||
3.6. Расположение двух плоскостей в пространстве |
|
Пусть плоскости и заданы общим уравнением: |
|
0 и |
0 |
соответственно. Рассмотрим случаи параллельности и перпендикулярности плоскостей.
Очевидно, если плоскости параллельны, то их нормальные векторы коллинеарны (рис. 3.22).
Если векторы коллинеарны, то их соответствующие координаты пропорциональны. Запишем нормальные векторы плоскостей:
; ; , ; ; .
Составим пропорции из координат нормальных векторов:
.
Полученное равенство является условием параллельности плоско-
стей. Оно означает, что если плоскости заданы общим уравнением, то условием их параллельности является пропорциональность коэффициентов перед переменными в общем уравнении.
127
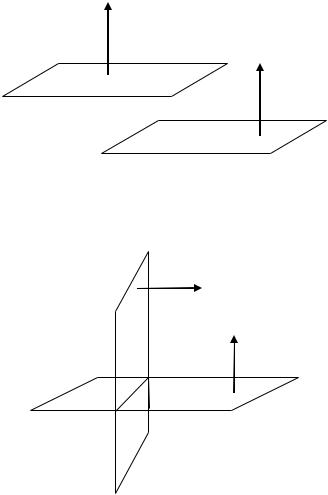
Рис. 3.22. Две параллельные плоскости и их нормальные векторы
Очевидно, если плоскости перпендикулярны, то их нормальные векторы перпендикулярны (рис. 3.23).
Рис. 3.23. Две перпендикулярные плоскости и их нормальные векторы
Если векторы перпендикулярны, то их скалярное произведение равно нулю: ∙ 0. Используя формулу нахождения скалярного произведения векторов через их координаты, получаем:
.
Полученное равенство является условием перпендикулярности плоско-
стей. Оно означает, что если плоскости заданы общим уравнением, то условием их перпендикулярности является равенство нулю суммы произведений коэффициентов перед соответствующими переменными в общем уравнении.
Пример 3.19. Установить, какие из следующих пар уравнений опре-
деляют параллельные плоскости: |
|
|
|
||||
1) 2 |
7 |
3 |
1 |
0, 4 |
14 |
2 |
5 0; |
2) 6 |
4 |
2 |
5 |
0, 3 |
2 |
|
2 0; |
3) 3 |
5 |
2 0, 2 |
4 |
1 0. |
|
|
|
Решение. Плоскости заданы общим уравнением. Поэтому условием их параллельности является пропорциональность коэффициентов перед переменными в общем уравнении плоскости.
1) Составляем пропорции: |
|
|
|
|
|
. Равенства неверные, поэтому |
|
|
|
||||
плоскости не параллельны. |
|
|
|
|
|
|
|
128 |
|
|
|
||

2) |
Составляем пропорции: |
|
|
|
|
|
|
|
. Равенства верные, поэтому |
||
|
|
|
|
||||||||
плоскости параллельны. |
|
|
|
|
|
|
|
|
|||
3) |
Составляем пропорции: |
|
|
|
|
|
|
|
. Равенство неверное, поэтому плос- |
||
|
|
|
|
|
|
||||||
кости не параллельны.
Ответ: 2).
Пример 3.20. Установить, какие из следующих пар уравнений опре-
деляют перпендикулярные плоскости: |
|
|
|||||
1) 9 |
3 |
2 |
8 0, 2 |
5 |
3 |
1 0; |
|
2) 4 |
|
3 |
3 0, 2 |
5 |
|
1 0; |
|
3) 8 |
4 |
5 0, |
3 |
2 |
2 0. |
||
Решение. Плоскости заданы общим уравнением. Поэтому условием их перпендикулярности является равенство нулю суммы произведений коэффициентов перед соответствующими переменными в общем уравнении плоскости.
|
1) Составляем сумму произведений коэффициентов перед соответ- |
|||||
ствующими переменными в общем уравнении плоскости: 9 ∙ 2 |
3 |
∙ 5 |
||||
|
2 ∙ 3 |
3 0. Условие перпендикулярности не выполняется, поэтому |
||||
плоскости не перпендикулярны. |
|
|
|
|||
|
2) Составляем сумму произведений коэффициентов перед соответ- |
|||||
ствующими переменными в общем уравнении плоскости: 4 ∙ 2 |
1 |
∙ 5 |
||||
3 ∙ |
1 |
0. Условие перпендикулярности выполняется, поэтому плоско- |
||||
сти перпендикулярны. |
|
|
|
|
||
|
3) Составляем сумму произведений коэффициентов перед соответ- |
|||||
ствующими переменными в общем уравнении плоскости: 8 ∙ 1 |
0 ∙ |
3 |
||||
4 ∙ |
2 |
0. Условие перпендикулярности выполняется, поэтому плоско- |
||||
сти перпендикулярны. |
|
|
|
|
||
|
Ответ: 2), 3). |
|
|
|
|
|
|
Пример 3.21. Определить, при каких значениях и плоскости |
|
||||
3 |
2 |
1 0 и 2 |
5 |
0 параллельны. |
|
|
|
Решение. Плоскости заданы общим уравнением. Поэтому условием |
|||||
их параллельности является пропорциональность коэффициентов перед переменными в общем уравнении плоскости. Составляем пропорции:
.
|
Запишем отсюда два равенства: |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Из первого равенства |
|
|
|
|
, из второго равенства |
|
|
. |
||||||||||
|
|
|
|
|
|
||||||||||||||
|
Ответ: |
|
|
, |
|
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
Пример 3.22. Определить, при каком значении плоскости 7 |
|
|||||||||||||||||
2 |
|
|
|
|
0 и |
3 |
1 0 перпендикулярны. |
|
|||||||||||
Решение. Плоскости заданы общим уравнением. Поэтому условием их перпендикулярности является равенство нулю суммы произведений коэффициентов перед соответствующими переменными в общем уравнении
129
