
917
.pdf
положительную сторону отрезок длины 7. Получим точку |
– проекцию |
||
точки на ось . В плоскости |
провед м через точки |
и пря- |
|
мые, параллельные координатной оси |
и отрезку |
соответственно. В |
|
пересечении этих прямых получаем точку (рис. 1.3).
7
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Рис. 1.3. Построение точки |
3; 5; 7 |
(К Примеру 1.1) |
|
|
|||||
|
Для построения точки |
4; |
2; 6 , отложим по оси |
в положитель- |
|||||||
ную сторону отрезок длины 4. Получим точку |
– проекцию точки |
|
на ось |
||||||||
. Далее отложим по оси |
в отрицательную сторону отрезок длины 2. |
||||||||||
Получим точку – проекцию точки |
на ось |
. В координатной плоскости |
|||||||||
|
провед м через точки |
и |
прямые, |
параллельные координатным |
|||||||
осям |
и |
соответственно. В пересечении этих прямых получаем точку |
|||||||||
– проекцию точки |
на координатную плоскость |
. Затем отложим по |
|||||||||
оси |
в положительную сторону отрезок длины 6. Получим точку |
|
– про- |
||||||||
екцию точки |
на ось |
. В плоскости |
провед м через точки |
и |
|||||||
прямые, параллельные координатной оси |
и отрезку |
|
соответ- |
||||||||
ственно. В пересечении этих прямых получаем точку |
(рис. 1.4). |
|
|
||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
2
4
Рис. 1.4. Построение точки 4; 2; 6 (К Примеру 1.1)
10
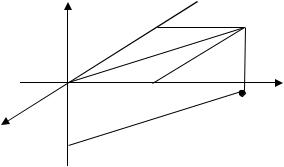
|
Для построения точки |
5; 4; |
3 |
отложим по оси |
в отрицатель- |
|||||
ную сторону отрезок длины 5. Получим точку |
– проекцию точки |
на ось |
||||||||
. Далее отложим по оси |
в положительную сторону отрезок длины 4. |
|||||||||
Получим точку – проекцию точки |
на ось |
. В координатной плоскости |
||||||||
|
провед м через точки |
и |
прямые, |
параллельные координатным |
||||||
осям |
и |
соответственно. В пересечении этих прямых получаем точку |
||||||||
– проекцию точки |
на координатную плоскость |
. Затем отложим по |
||||||||
оси |
в отрицательную сторону отрезок длины 3. Получим точку С |
– про- |
||||||||
екцию точки |
на ось |
. В плоскости |
|
провед м через точки С |
и С |
|||||
прямые, параллельные координатной оси |
и отрезку |
С |
соответственно. |
|||||||
В пересечении этих прямых получаем точку |
|
|
|
|
||||||
(рис. 1.5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Рис. 1.5. Построение точки |
5; 4; |
3 |
(К Примеру 1.1) |
|
|||||||
|
Для построения точки |
6; 8; |
5 |
отложим по оси |
в отрица- |
|||||||
тельную сторону отрезок длины 6. Получим точку |
– проекцию точки |
|||||||||||
на ось |
. Далее отложим по оси |
в отрицательную сторону отрезок длины |
||||||||||
8. Получим точку |
– проекцию точки |
на ось . В координатной плос- |
||||||||||
кости |
провед м через точки |
и |
прямые, параллельные координат- |
|||||||||
ным осям |
и |
соответственно. В пересечении этих прямых получаем |
||||||||||
точку |
– проекцию точки |
на координатную плоскость |
. Затем отло- |
|||||||||
жим по оси |
в отрицательную сторону отрезок длины 5. Получим точку |
|||||||||||
– проекцию точки на ось . В плоскости |
|
провед м через точки |
||||||||||
и |
прямые, параллельные координатной оси |
и отрезку |
соот- |
|||||||||
ветственно. В пересечении этих прямых получаем точку |
|
|
|
|||||||||
(рис. 1.6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как координата |
точки |
0; |
6; 4 |
равна нулю, то точка лежит в |
|||||||
плоскости |
. Для построения точки |
0; |
6; 4 отложим по оси |
в от- |
||||||||
рицательную сторону отрезок длины 6. Получим точку |
– проекцию точки |
|||||||||||
на ось . Далее отложим по оси |
в положительную сторону отрезок |
|||||||||||
длины 4. Получим точку |
– проекцию точки |
на ось |
. В координатной |
|||||||||
плоскости |
провед м через точки |
и |
прямые, параллельные коорди- |
|||||||||
натным осям |
и |
соответственно. В пересечении этих прямых получаем |
||||||||||
точку |
(рис. 1.7). |
|
|
|
|
|
|
|
|
|
|
|
11
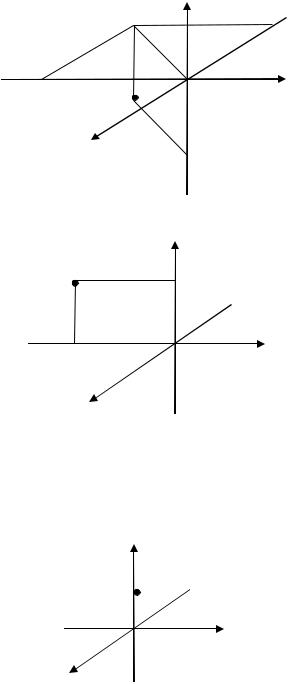
6
8
5
Рис. 1.6. Построение точки |
6; 8; 5 (К Примеру 1.1) |
4
6 |
|
|
|
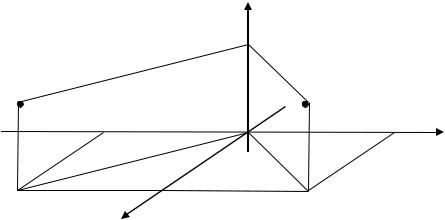
Рис. 1.7. Построение точки |
0; |
6; 4 |
(К Примеру 1.1) |
Так как координаты и точки |
0; 0; 1 |
равны нулю, то точка лежит |
|
на оси . Для построения точки 0; 0; 1 |
отложим по оси в положитель- |
||
ную сторону отрезок длины 1. Получим точку |
(рис. 1.8). |
||
1 |
|
|
|
Рис. 1.8. Построение точки |
0; 0; 1 (К Примеру 1.1) |
|
|
||||
Пример |
1.2. Найти |
координаты проекций |
точек |
7; 2; 9 , |
|||
1; 3; 4 , |
6; 0; 2 |
, |
5; 0; 0 на: 1) плоскость |
; 2) плоскость |
; |
||
3) плоскость |
; 4) ось |
; 5) ось |
; 6) ось . |
|
|
|
|
Решение. |
|
|
|
|
|
|
|
1) Для нахождения координат проекций точек на плоскость |
|
при- |
|||||
равняем координату точек к нулю. Получаем следующие координаты про-
екций точек: |
7; 2; 0 , |
1; 3; 0 , |
6;0; 0 , |
5; 0; 0 . |
12
|
|
2) Для нахождения координат проекций точек на плоскость |
при- |
|||||||||||
равняем координату |
точек к нулю. Получаем следующие координаты про- |
|||||||||||||
екций точек: |
7; 0; 9 , |
1; 0; |
4 , |
6;0; 2 , |
5; 0; 0 . |
|
||||||||
|
|
3) Для нахождения координат проекций точек на плоскость |
при- |
|||||||||||
равняем координату |
точек к нулю. Получаем следующие координаты про- |
|||||||||||||
екций точек: |
0;2; 9 , |
0; |
3; |
4 , |
0; 0; 2 , |
0;0; 0 . |
|
|||||||
|
|
4) Для нахождения координат проекций точек на ось |
приравняем |
|||||||||||
координаты |
и |
точек к нулю. Получаем следующие координаты проекций |
||||||||||||
точек: |
|
7; 0; 0 , |
1; 0; 0 , |
6; 0; 0 , |
5; 0; 0 . |
|
|
|||||||
|
|
5) Для нахождения координат проекций точек на ось |
приравняем |
|||||||||||
координаты |
и |
точек к нулю. Получаем следующие координаты проекций |
||||||||||||
точек: |
0; 2; 0 , |
0; 3; 0 , |
0; 0; 0 , |
0; 0; 0 . |
|
|
|
|||||||
|
|
6) Для нахождения координат проекций точек на ось |
приравняем |
|||||||||||
координаты |
и |
точек к нулю. Получаем следующие координаты проекций |
||||||||||||
точек: |
0; 0; 9 , |
0; 0; |
4 , |
0; 0; 2 , |
0; 0; 0 . |
|
|
|
||||||
|
|
Ответ: 1) |
|
7; 2; 0 , |
1; |
|
3; 0 , |
6; 0; 0 , |
5; 0; 0 ; |
|||||
2) |
|
7; 0; 9 , |
1; 0; |
4 , |
|
|
6; 0; 2 , |
5;0; 0 ; 3) |
|
0; 2; 9 , |
||||
|
0; |
3; |
4 , |
|
0;0; 2 , |
0; 0; 0 ; |
4) |
|
7; 0; 0 , |
|
1; 0; 0 , |
|||
|
6; 0; 0 , |
5; 0; 0 ; 5) |
0; 2; 0 , |
0; |
3; 0 , |
|
0;0; 0 , |
0;0; 0 ; |
||||||
6) |
0; 0; 9 , |
0; 0; |
4 , |
0;0; 2 , |
|
0;0; 0 . |
|
|
|
|
||||
|
|
Пример |
1.3. Найти координаты |
точки, |
симметричной |
точке |
||||||||
|
5; |
7; 4 относительно плоскости |
|
. |
|
|
|
|
|
|||||
|
|
Решение. Абсцисса и аппликата точки, симметричной относительно |
||||||||||||
плоскости |
, совпадают, а ордината отличается знаком. Поэтому искомая |
|||||||||||||
точка имеет следующие координаты: |
|
5; 7; 4 . Нахождение точек, симмет- |
||||||||||||
ричных относительно чего-либо удобно определять графически |
|
|
||||||||||||
(рис. 1.9). |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
7 |
7 |
|
5 |
|
|
Рис. 1.9. Построение точки, симметричной точке |
5; 7; 4 относительно |
||
|
плоскости |
(К Примеру |
1.3) |
Ответ: |
5; 7; 4 . |
|
|
13

1.3. Расстояние между двумя точками в пространстве
Пусть ; ; и ; ; – две данные точки пространства. Расстояние между этими точками равно длине диагонали прямоугольного параллелепипеда, грани которого параллельны координатным плоскостям и
проходят через точки |
и |
; а также равно длине направленного отрезка |
(рис. 1.10). |
|
|
|
Рис. 1.10. Расстояние между двумя точками в пространстве |
|
|
||||||||||||
Расстояние между точками |
|
и |
|
обозначим через |
. |
Из прямо- |
|||||||||
угольного треугольника |
|
|
по теореме Пифагора получаем: |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
| |
| |
| |
| . |
|
|
|
|
|
|
|
|
|
|
Выразим | |
| |
через координаты точек |
и |
. |
Спроектируем |
||||||||||
точки |
и |
на координатные оси |
|
и |
. Для этого опустим из этих |
||||||||||
точек перпендикуляры на координатную плоскость |
. Основания перпен- |
||||||||||||||
дикуляров обозначим |
|
и |
соответственно. Затем из точек |
и |
|||||||||||
опустим перпендикуляры на ось |
|
. Основания перпендикуляров обо- |
|||||||||||||
значим |
и |
|
соответственно. Это и будут проекции точек |
и |
на |
||||||||||
ось . Далее из точек |
|
и |
опустим перпендикуляры на ось |
. Ос- |
|||||||||||
нования перпендикуляров обозначим |
|
и |
соответственно. Это и будут |
||||||||||||
проекции точек |
и |
на ось |
. Учитывая, что | |
| |
|
|
|
|
|||||||
| |
|, |
|
|
|
| |
|
|, |
из |
|
прямоугольного |
|
треугольника |
|||
|
по теореме Пифагора получаем: |
|
|
|
|
|
|
||||||||
|
|
|
| |
|
| |
|
|
|
|
|
| |
|
| |
|
|
|
|
| |
| |
|
| |
|
| |
|
|
|
|
|
. |
|
|
Выразим | |
| |
через координаты точек |
и |
. |
Спроектируем |
||||||||||
точки |
и |
на координатную ось |
|
. Для этого опустим из этих точек |
|||||||||||
перпендикуляры на координатную ось |
|
. Основания перпендикуляров обо- |
|||||||||||||
значим |
и |
|
соответственно. Учитывая, что | |
| |
|
| |
|
|. По- |
|||||||
лучаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
| |
| |
|
| |
|
| |
| |
|
| |
|
|
. |
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|

Тогда расстояние между точками |
и : |
||||||
|
|
|
|
|
|
|
|
| |
| | |
| |
|
|
. |
||
Таким образом: |
|
|
|
|
|
||
.
Полученная формула означает, что расстояние между двумя точками равно квадратному корню из суммы квадратов разностей соответствую-
щих координат точек. |
|
Пример 1.4. Найти расстояние между точками |
1; 2; 3 и |
3; 1; 9 .
Решение. Воспользуемся формулой расстояния между двумя точ-
ками. Здесь |
1, |
3, |
2, |
1, |
3, |
|
9. Получаем: |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 1 |
|
1 |
2 |
9 |
3 |
|
√4 9 |
36 7. |
||||
|
Ответ: |
7. |
|
|
|
|
|
|
|
|
|
|
|
Пример 1.5. Доказать, |
что треугольник с вершинами 3; 1; 2 , |
||||||||||
0; 4; 2 , |
|
3; 2; 1 равнобедренный. |
|
|
|
|
|
|||||
|
Решение. |
Треугольник является равнобедренным, если длины двух |
||||||||||
его сторон равны. Найд м длину каждой стороны треугольника по формуле расстояния между двумя точками:
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
4 |
1 |
2 |
2 |
√9 |
9 |
0 |
|
3√2; |
||||||
| | |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
3 |
2 |
1 |
1 |
2 |
√36 9 |
1 |
√46; |
||||||||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
0 |
2 |
4 |
1 |
2 |
√9 |
36 |
1 |
√46. |
|||||||
Так как | | | |, то треугольник является равнобедренным. |
|||
Пример 1.6. Определить, есть ли тупой угол среди внутренних углов |
|||
треугольника с вершинами |
4; 1; 4 , |
0; 7; 4 , |
3; 1; 2 . |
Решение. Для выявления тупого угла треугольника нам понадобятся |
|||
длины сторон треугольника. Найд м длину каждой стороны треугольника по формуле расстояния между двумя точками:
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
4 |
7 |
1 |
4 |
4 |
√16 64 64 |
|
||||||||
12; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
4 |
1 |
1 |
2 |
4 |
√1 |
4 36 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√41; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
0 |
1 |
7 |
2 |
4 |
√9 |
36 4 |
|
7. |
||||||
Далее воспользуемся теоремой косинусов. Предварительно выполним
схематичное построение треугольника (рис. 1.11). |
|
|
|||||
Применим теорему косинусов к стороне |
|
: |
|
||||
| |
| |
| |
| | |
| 2 ∙ | |
| ∙ | |
| ∙ cos |
. |
|
|
|
|
15 |
|
|
|
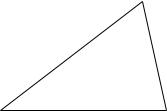
Рис. 1.11. Треугольник (к Примеру 1.6).
Выразим отсюда cos |
: |
|
|
||
cos |
| |
| | |
| | |
| |
. |
|
∙| |
|∙| |
| |
||
|
|
|
|||
Подставим числовые значения длин сторон треугольника:
cos |
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
∙√ |
∙ |
|
|
|
|
|
√ |
√ |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Так как cos |
|
|
|
|
|
|
отрицателен, то |
|
|
|
|
|
|
тупой. |
||||||||||||||||||||
Ответ: |
|
|
|
|
тупой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 1.7. На оси ординат найти точку, равноудал нную от точек |
||||||||||||||||||||||||||||||||||
1; 3; 7 |
|
и 5; 7; |
5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. |
Пусть |
0; |
; 0 |
|
– искомая точка. Запишем расстояние |
|||||||||||||||||||||||||||||
между точками |
и , используя формулу расстояния между двумя точками: |
|||||||||||||||||||||||||||||||||
| |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
0 |
|
|
|
|
|
|
3 |
|
|
7 |
0 |
|
|
|
50 |
3 . |
||||||||||||||
Аналогично запишем расстояние между точками |
и : |
|||||||||||||||||||||||||||||||||
| |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
5 |
0 |
|
7 |
|
|
|
|
5 |
0 |
|
|
|
50 |
7 . |
|||||||||||||||||
По условию точка |
|
|
|
равноудалена от точек |
|
|
и , то есть расстояние |
|||||||||||||||||||||||||||
между точками |
и равно расстоянию между точками |
и . Приравни- |
||||||||||||||||||||||||||||||||
ваем полученные выше выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
50 |
|
|
|
3 |
|
|
|
50 |
|
|
|
7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Возвед м обе части равенства в квадрат: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
50 |
|
|
|
|
3 |
50 |
|
|
|
|
|
7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Преобразуем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6 |
|
9 |
|
|
14 |
|
|
|
49, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
20 |
40, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Искомая точка: |
0; 2; 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ответ: |
0; 2; 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.4. Деление отрезка в заданном отношении в пространстве |
||||||||||||||||||||||||||||||||||
Пусть |
; |
; |
|
|
|
и |
|
|
; |
|
; |
|
|
– две данные точки пространства |
||||||||||||||||||||
и известно, что некоторая точка |
; |
; |
|
|
делит отрезок |
в отношении |
||||||||||||||||||||||||||||
, то есть |
|
|
|
|
. Здесь |
|
и |
|
|
– величины направленных отрезков |
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
и.
16
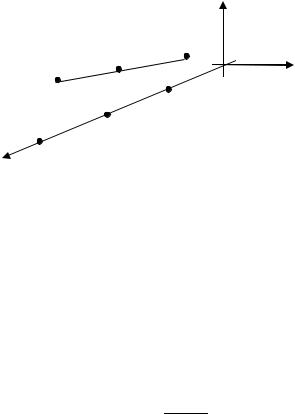
|
Получим формулы для вычисления координат точки . Спроектируем |
||||||||||
точки |
, |
, |
на ось |
. Для этого провед м через эти точки плоскости |
|||||||
перпендикулярно оси |
. Точки пересечения плоскостей с осью |
обозна- |
|||||||||
чим |
, |
, |
соответственно (рис. 1.12). Эти точки представляют про- |
||||||||
екции точек |
, |
, на ось . |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.12. Нахождение абсциссы точки , которая делит отрезок в заданном отношении
Так как отрезки прямых, заключ нные между параллельными плоско-
стями, пропорциональны, то можно записать: |
|
|
|
. Но |
|||
|
|
||||||
, |
. Тогда: |
|
. Выразим отсюда |
: |
|||
|
|||||||
1
.
Полученная формула позволяет вычислить координату точки . Аналогично рассуждая, можно получить формулы для координат и
точки .
Таким образом, получаем следующие формулы для нахождения коор-
динат |
точки |
; ; |
, |
которая |
делит отрезок между |
точками |
|||||||||||||||
; |
; |
и |
; |
; |
|
в отношении |
: |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
, |
|
|
|
|
|
, |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассмотрим частный случай, когда точка |
является серединой от- |
||||||||||||||||||||
резка |
|
. Тогда |
|
|
|
и |
1. Формулы нахождения координат |
||||||||||||||
середины отрезка принимают вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
, |
|
|
|
|
, |
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, координаты середины отрезка равны полусумме со- |
|||||||||||||||||||||
ответствующих координат его концов. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 1.8. Даны две точки |
9; |
3; 1 и |
6; 8; 5 . Найти коор- |
||||||||||||||||||
динаты середины отрезка |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Воспользуемся формулами нахождения координатсере- |
|||||||||||||||||||||
дины отрезка через координаты его концов. Здесь |
9, |
6, |
3, |
||||||||||||||||||
8, |
|
1, |
5. Найд м абсциссу середины отрезка: |
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
. Найд м ординату середины отрезка: |
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Найд м аппликату середины отрезка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Ответ: |
|
|
; |
|
|
; 3 . |
|
|
|
|
|
|
|
|
4; 3; 1 |
|
|
|
|
5; |
2; |
6 . Найти ко- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
Пример 1.9. Даны две точки |
и |
||||||||||||||||||||||||||||||||||||||||||||||||||
ординаты точки |
|
, которая делит отрезок |
в отношении |
|
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Решение. Воспользуемся формулами нахождения координат точки, |
|||||||||||||||||||||||||||||||||||||||||||||||||||
которая делит отрезок в заданном отношении. Здесь |
|
|
4, |
5, |
3, |
||||||||||||||||||||||||||||||||||||||||||||||||
2, |
|
|
1, |
|
|
|
|
|
|
6. Найд м абсциссу точки : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
∙ |
2. Найд м ординату точки |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
. Найд м |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
аппликату точки |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Ответ: |
|
2; |
|
|
; |
|
|
. |
|
|
|
|
|
|
2; 3; |
5 , |
|
|
1; 3; 2 параллело- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
Пример 1.10. Даны две вершины |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
грамма |
|
|
и точка пересечения его диагоналей |
4; |
|
|
|
1; 7 . Определить |
|||||||||||||||||||||||||||||||||||||||||||||
две другие вершины этого параллелограмма. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
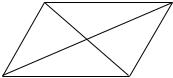
Решение. Выполним схематичный черт ж (рис. 1.13). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
Рис. 1.13. Параллелограмм |
(к Примеру 1.10) |
|
|
|
||
Известно, что диагонали параллелограмма в точке пересечения де- |
|||||||
лятся пополам. Поэтому точка является серединой отрезка |
. Воспользу- |
||||||
емся формулой для нахождения абсциссы середины отрезка: |
|
|
. По |
||||
|
|
||||||
условию |
4, |
2. Подставляем: 4 |
|
. Отсюда |
6. Затем вос- |
||
|
|||||||
пользуемся формулой для нахождения ординаты середины отрезка:
|
|
. По условию |
1, |
3. Подставляем: 1 |
|
|
|
. Отсюда |
||||
|
|
|
|
|||||||||
|
1. И воспользуемся формулой для нахождения аппликаты середины от- |
|||||||||||
резка: |
|
|
. По условию |
7, |
5. Подставляем: 7 |
|
. От- |
|||||
|
|
|
||||||||||
сюда |
19. Таким образом, вершина параллелограмма |
6; 1; 19 . |
|
|||||||||
|
|
Аналогично найд м другую вершину |
параллелограмма. Точка |
яв- |
||||||||
ляется серединой отрезка . Воспользуемся формулой для нахождения абс-
циссы середины отрезка: |
|
. По условию |
4, |
1. Подстав- |
||||
|
||||||||
ляем: 4 |
|
. Отсюда |
9. Затем воспользуемся формулой для нахож- |
|||||
|
||||||||
дения ординаты середины отрезка: |
18 |
|
. По условию |
1, |
||||
|
||||||||
|
|
|
|
|
|
|
|
|
3. Подставляем: 1 |
|
. Отсюда |
5. И воспользуемся формулой |
||||||
|
|||||||||
для нахождения аппликаты середины отрезка: |
|
|
. По условию |
||||||
|
|
||||||||
7, |
2. Подставляем: 7 |
|
|
. Отсюда |
|
12. Таким образом, вершина |
|||
|
|
|
|||||||
параллелограмма 9; 5; 12 . |
|
|
|
|
|||||
|
Ответ: 6; 1; 19 , |
9; 5; 12 . |
|
|
|
|
|||
|
Пример 1.11. Даны вершины треугольника 1; 2; 1 , 2; 1; 3 и |
||||||||
4; 7; 5 . Вычислить длину биссектрисы его внутреннего угла при вер- |
|||||||||
шине . |
|
|
|
|
|
|
|
||
|
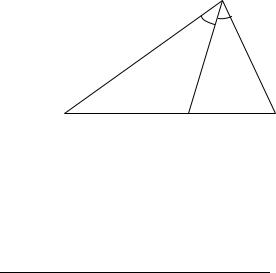
Решение. Обозначим точку пересечения биссектрисы со стороной |
||||||||
через |
(рис. 1.14). |
|
|
|
|
|
|
|
|
Рис. 1.14. Треугольник |
и биссектриса |
(к Примеру 1.11) |
Известно, что биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторо-
|
| |
| |
| |
| |
||
нам. Можно записать соотношение: |
|
|
|
|
|
. |
| |
| |
|
| |
| |
||
По формуле расстояния между двумя точками:
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 1 |
|
|
|
|
1 2 |
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
√26, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
4 2 |
|
7 |
|
|
|
1 |
|
|
5 |
3 |
|
|
|
|
|
|
√104 |
|
|
|
2√26. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Тогда |
|
√ |
|
|
, то есть точка |
|
делит отрезок |
|
|
|
в отношении |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
√ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
. Найд м координаты точки |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
; 1 . |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
Точка пересечения биссектрисы и стороны |
: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Вычислим длину биссектрисы |
, |
используя формулу расстояния |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
между двумя точками: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
19
