Задачи для самостоятельного решения:
1) Вычислите двойные интегралы, взятые по прямоугольным областям интегрирования D, заданным условиями в скобках:
а) 
(Ответ: /12);
б) 
(Ответ: – 2);.
2
) Представьте
двойной интеграл
,
где D
– области, указанные на рис. 3.2 а,
б,
в,
г,
в виде суммы двукратных интегралов
(с наименьшим числом слагаемых). Фигуры,
показанные на рис. 3.2 в,
г,
составлены из прямых линий и дуг
окружностей.
3) Вычислите
двойной интеграл
,
если D
– область, ограниченная параболам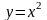и
и
(Ответ: 33/140).
4) Вычислите
двойной интеграл
,
если D
– область, ограниченная линиями
и
,
.
5) Вычислите
двойной интеграл
,
если D
– параллелограмм, ограниченный прямыми
,
,
,
.
6) Вычислите
двойной интеграл
,
если D
– треугольник с вершинами в точках:
O(0; 0),
A(0; 1),
B(1; 1).
Можно ли вычислить данный интеграл,
сводя его к повторному первым способом
(случай 2.1)?
вторым способом (случай 2.2)?
7) Вычислите
двойной интеграл
по области D,
заключенной между двумя квадратами
с центрами в начале координат и
сторонами, параллельными осям координат,
если сторона внутреннего квадрата равна
2, а внешнего – 4.
Фрагменты рабочей тетради по теме «Степенные ряды»
Проведите доказательство формулы Эйлера
с помощью степенных рядов.
Воспользуйтесь разложениями в ряд Маклорена следующих элементарных функций:
,
(3.1)
,
(3.2)
.
(3.3)
Эти разложения справедливы для любой точки x числовой прямой.
Замените в выражении (3.1) x на ix с учетом того, что
,
,
,
для 
.
,
.
(3.4)
Сравните правые части выражений (3.4), (3.2), (3.3).
Исторические сведения:
Степенные ряды начали широко использоваться в математике с работ И. Ньютона.
Формула бинома Ньютона для натурального показателя
,
где
,
была известна задолго до рождения
великого ученого.
Его заслуга заключалась в распространении этого результата на дробные показатели. По аналогии с известной формулой он пришел к равенству
,
для
произвольного рационального r.
Строгое доказательство этой формулы
было дано значительно позже (1811) Гауссом.
Для натурального показателя, т.е. для
,
коэффициенты
при 
,
поэтому в правой части остается
многочлен. Но если r
не является натуральным числом, этого
не происходит и правая часть
представляет собой бесконечную сумму
степенных функций.
Бесконечную сумму степенных функций с произвольными действительными коэффициентами называют степенным рядом.
Рассмотрим ряд, составленный из членов геометрической прогрессии:
.
Ее
знаменатель
.
Ряд сходится при 
.
Интегрируя обе части равенства на отрезке
[0; x],
,
получим:
.
С другой
стороны,
.
В результате имеем разложение в степенной ряд еще одной функции:
.
(3.5)
Оно
справедливо для всех
.
Разложение это впервые встречается в «Научном сборнике» (1501) индийского математика Нилоканты в виде
.
При x = 1 разложение (3.5) превращается в равенство
.
(3.6)
Этот ряд позволяет вычислить число с любой степенью точности, однако сделать это трудно: ряд (3.6) сходится очень медленно.
Например, для получения значения с точностью до 0,01 надо вычислить сумму 50 первых слагаемых (докажите самостоятельно). Эйлер для устранения этого недостатка использовал тождество
.
Полученные ряды
,
.
сходятся гораздо быстрее ряда (3.6). Покажите самостоятельно, что достаточно взять только по три первых слагаемых этих рядов, чтобы получить значение с двумя верными знаками после запятой.
Фрагмент
рабочего документа MathCAD
с исследованием
ряда Маклорена
для функции
Построены
график функции
и графики многочленов пятой степени
(взяли первые три члена ряда) и пятнадцатой
степени (взяли первые восемь членов
ряда).
По рисунку видно, что приближение функции рядом Маклорена имеет локальный характер: функция хорошо аппроксимируется частичными суммами ряда Маклорена в окрестности точки 0. Аппроксимация тем лучше, чем больше членов ряда мы берем.
Задание. Исследуйте графически поведение заданной функции и частичных сумм ее ряда Маклорена.
Применение рабочих тетрадей при работе со студентами позволяет преподавателю:
– усилить наглядность и «яркость» обучения (в тетради содержится наглядный материал в виде опорных конспектов, схем, таблиц, рисунков и т. п., задания на упорядочение информации, на построение графиков и др.);
– расширить виды деятельности на занятии (преподаватель может вести диалог со студентами, вовлекать их в дискуссию, побуждать к рассуждениям, совместному доказательству и выводам; осуществлять обучение через игровую или практическую деятельность; проводить контроль над качеством усвоения изучаемого материала);
– учесть индивидуальные особенности студентов (студент имеет возможность выбирать задания, которые соответствуют его творческому потенциалу).
Комплект рабочих тетрадей по высшей математике призван оказать студентам младших курсов реальную помощь в выполнении заданий по ряду сложных разделов высшей математики, научить их самостоятельно работать и тем самым повысить качество получаемого студентами образования, активизировать познавательную самостоятельность студентов.