Элементы квантовой механики
18.1. Волны де Бройля
Объектами изучения квантовой механики являются атомы, молекулы, а также атомные ядра и элементарные частицы. Одной из основ квантовой механики является идея де Бройля о том, что корпускулярно-волновой дуализм свойственен не только световым частицам – фотонам, но и частицам вещества, имеющим массу – электронам, протонам, нейтронам, атомам, молекулам и атомным ядрам. Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой – волновые характеристики – частота и длина волны λ. Со всякой частицей, имеющей массу m, которая движется со скоростью υ, связано распространение волны де Бройля λ:
.
(18.1.1)
Здесь h – постоянная Планка, p = mυ – импульс движущейся частицы. Волны де Бройля не являются электромагнитными волнами и не имеют аналогии среди всех видов волн, изучаемых в классической физике.
18.2. Соотношения неопределенностей
Для волны любой природы представление о том, что она имеет некоторые координаты, находится в определенном месте пространства, лишено физического смысла. Например, если волна, распространяющаяся по поверхности воды, достигла лодки, то не имеет смысла утверждать, что волна находится только в том месте, где она встретилась с лодкой. Когда частица, обладающая волновыми свойствами, движется вдоль некоторой оси, например оси ОX, ее координата на этой оси может быть определена лишь с точностью до величины Δх, называемой неопределенностью координаты частицы. Неопределенностью импульса частицы называется величина Δр, определяемая соотношением
.
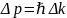(18.2.1)
Соотношение неопределенностей Гейзенберга:
.
(18.2.2)
Здесь
k
волновое число,
,
Δx,
Δу
и
Δz
— неопределенности координат частицы
по осям ОX,
ОY,
ОZ;
Δрх,
Δру,
Δрz
—
неопределенности проекций импульса
частицы по тем же осям, микрочастица не
может иметь одновременно определенную
координату (x,y,z)
и определенную соответствующую проекцию
импульса (рх,
ру,
рz).
Соотношение
неопределенностей допускает обращение
в нуль неопределенности одной из величин,
например Δр=0.
Это означает, что частица имеет строго
определенное значение импульса р
(или скорости υ),
но тогда Δх=∞.
Следовательно, положение частицы на
оси ОX
(ее
координата) становится совершенно
неопределенным: частицу можно обнаружить
в любом месте на оси ОX
в
пределах от 0 до ∞.
В связи с тем, что у макроскопических тел волновые свойства не обнаруживаются, соотношение неопределенностей не накладывает для таких тел никаких ограничений на возможность определения их координат и импульсов. Макроскопическое тело, движущееся по оси ОX, может одновременно иметь точные значения координаты и импульса.
18.3. Общее уравнение Шредингера
Уравнение Шредингера является уравнением движения в квантовой механике. Это уравнение является волновым уравнением, т.е. оно учитывает волновые свойства частиц. Оно не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом, что придает ему характер закона природы. Уравнение Шредингера имеет вид
,
(18.3.1)
где
,
m
– масса частицы, Δ
– оператор Лапласа, i
– мнимая единица, U(x,y,z)
– потенциальная функция частицы в
силовом поле, в котором она движется,
– оператор
Лапласа (Ψ
=
),
Ψ
–
искомая волновая функция частицы (Ψ
= Ψ(x,y,z,t)).
Уравнение (18.3.1) справедливо для любой
частицы, движущейся со скоростью υ<<c.
Оно дополняется условиями, накладываемыми
на волновую функцию:
волновая функция должна быть конечной, однозначной и непрерывной;
производные должны быть непрерывны;
функция
должна быть интегрируема.
Для многих физических явлений, происходящих в микромире, можно найти уравнение Шредингера для стационарных состояний – состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором движется частица, стационарно, т.е. функция U = U(x,y,z) не зависит явно от времени и имеет смысл потенциальной энергии. В этом случае уравнение Шредингера будет иметь вид
.
(18.3.2)
Здесь ψ=ψ(x,y,z) – волновая функция, не зависящая от времени, E – полная энергия частицы, постоянная в случае стационарного поля.
Решением уравнения Шредингера для стационарных состояний являются волновые функции – конечные однозначные и непрерывные вместе со своими первыми производными.