3.4 Проверка статистических гипотез. Проверка гипотез о законе распределения

Информация, полученная по выборке, может быть использована для оценки правомерности некоторых предположений (гипотез) о генеральной совокупности.

Статистической гипотезой называют любое утверждение о виде или свойствах распределения наблюдаемых в эксперименте случайных величин.

Гипотезы о неизвестном параметре Θ распределения бывают простые (Θ = Θ₀) и сложные (Θ < Θ₀, Θ > Θ₀, Θ ≠ Θ₀).

Проверяемую гипотезу обозначают H₀, альтернативную – H₁. Гипотезу проверяют на основании выборки. Случайный характер выборки может приводить к ошибкам. Ошибка первого рода имеет место тогда, когда отвергается верная гипотеза H₀. Вероятность такой ошибки называется уровнем значимости и обозначается α. Чем меньше α, тем меньше вероятность отклонить верную гипотезу.

При ошибке второго рода отвергается верная на самом деле альтернативная гипотеза – H₁ (принимается неверная гипотеза H₀). Вероятность этой ошибки обозначают через β, а (1–β) называется мощностью критерия. Обычно при заданном уровне значимости α отыскивается критерий с наибольшей мощностью.

Проверка статистической гипотезы состоит из следующих этапов:

• определение гипотез H₀ и H₁;

• выбор статистики критерия (испытывать гипотезу можно на основе любой статистики, имеющей любое вероятностное распределение) и задание уровня значимости α;

• по статистике критерия и уровню значимости α определяют границу (квантиль), определяющую критическую область (т.е. область отклонения гипотезы H₀);

• по выборке подсчитывают значение критерия;

• если фактически наблюдаемое значение критерия попадает в критическую область, то основная гипотеза H₀ отклоняется и принимается H₁.

Проверка гипотез о законе распределения

Рассмотрим, как можно проверить гипотезу о распределении генеральной совокупности.

Пусть (x₁, x₂, … x_m) – выборка из генеральной совокупности ξ с неизвестной функцией распределения, о которой выдвинута простая гипотеза H₀: F_ξ(x)=F(x), где F(x) полностью задана. Это распределение назовем теоретическим. Альтернативное распределение в данном случае не конкретизируется и речь идет просто о согласии данных и гипотезы H₀.

Для проверки таких гипотез разработано несколько критериев согласия, раиболее известным является критерий Пирсона (χ²: хи-квадрат). При использовании χ² –критерия вся область изменения генеральной совокупности делится на m интервалов (которые могут иметь различную длину). По выборке по этим же интервалам составляется статистический ряд (x_i → n_i, где n – объем выборки: ) и вычисляются оценки параметров теоретического распределения. Тем самым теоретическое распределение будет полностью определено. Теперь по теоретическому распределению подсчитывают вероятности p_i того, что случайная величина X принимает значения из i-го интервала по формуле

P(α≤X≤β) = F(β)–F(α).

По найденным p_i ищутся теоретические частоты (m_i=n·p_i).

Гипотеза H₀ верна, если теоретические (m_i) и эмпирические (n_i) частоты достаточно мало отличаются друг от друга. В 1900 году К. Пирсон предложил использовать в качестве меры отклонения эмирических данных (n_i) от гипотетических значений (m_i) следующую статистику

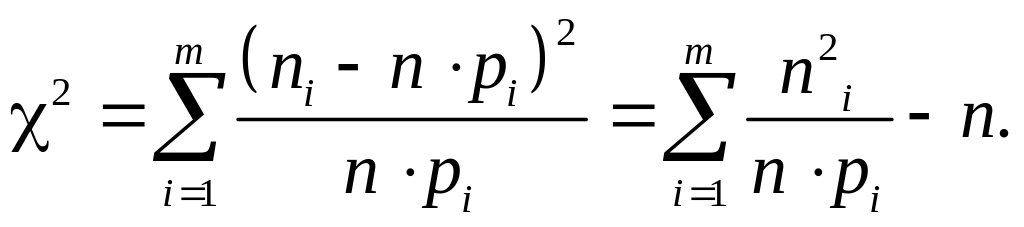
Согласно теореме Пирсона эта величина при имеет χ² – распределение с числом степеней свободы (k=m–r–1), m – число интервалов выборки, r – число параметров гипотетического распределения. Чем больше χ², тем хуже согласованы теоретическое и эмпирическое распределения.

Поскольку относительная частота события является состоятельной оценкой его вероятности, то при больших n разности в сумме должны быть малы и, следовательно, значение статистики не должно быть слишком большим. При достаточно большом значении χ² нужно отвергнуть гипотезу H₀. Поэтому естественно задать только правостороннюю критическую область для гипотезы H₀ в виде , где критическая граница t_α при заданном уровне значимости α должна быть выбрана из условия

Пример 32. Пользуясь критерием согласия Пирсона, проверить при уровне значимости α=0,01 гипотезу H₀ о том, что случайная величина X, статистический ряд которой приведен в таблице, распределена по нормальному закону.

Интервалы значений xi	(-4, -3)	(-3, -2)	(-2, -1)	(-1, 0)
Относительные частоты pi*	0,012	0,050	0,144	0,266
Интервалы значений xi	(0, 1)	(1, 2)	(2, 3)	(3, 4)
Относительные частоты pi*	0,240	0,176	0,092	0,020

Решение. Для вычисления вероятностей p_i необходимо вычислить параметры, определяющие нормальный закон распределения (a и σ). Их оценки, рассчитанные по выборке объемом n = 500, дадут значения и .

Используя формулу

,

находим для каждого i-го интервала вероятность p_i (вероятность попадания в i-й интервал случайной величины X, подчиненной нормальному закону распределения с параметрами , ) и результат оформим таблицей.

Интервалы значений xi	(-4, -3)	(-3, -2)	(-2, -1)	(-1, 0)
Вероятности pi	0,0126	0,0522	0,1422	0,2433
Интервалы значений xi	(0, 1)	(1, 2)	(2, 3)	(3, 4)
Вероятности pi	0,2668	0,1789	0,0770	0,0212

По данным двух таблиц вычислим наблюдаемое значение статистики Пирсона χ² . Получим χ² = 3,99.

Теперь определяем число степеней свободы k; так как количество интервалов равно m=8, а число параметров нормального распределения r=2, то k=8–2–1=5. По таблице распределения Пирсона для k=5 и α=0,01 найдем Так как , то нет оснований отвергать проверяемую гипотезу.