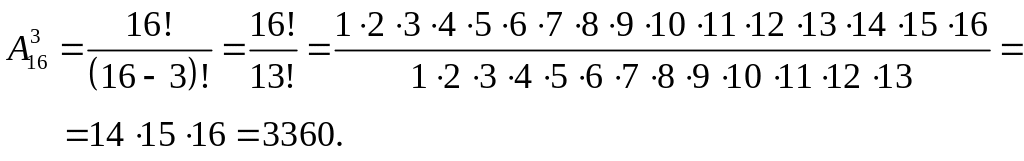Вероятностное пространство

(случай конечного или счетного числа исходов)

Введем аксиому (для случая конечного или счетного пространства элементарных исходов). Каждому элементарному исходу _i пространства  соответствует некоторая неотрицательная числовая характеристика P_i шансов его появления, называемая вероятностью исхода _i , причем

(здесь суммирование ведется по всем i, для которых выполняется условие: _i). Отсюда следует, что 0  P_i  1для всех i.

Вероятность любого события А определяется как сумма вероятностей всех элементарных исходов, благоприятствующих событию  А. Обозначим ее Р(А).

(1)

Отсюда следует, что

0P(A)1;

P()=1;

P()=0.

Будем говорить, что задано вероятностное пространство, если задано пространство элементарных исходов  и определено соответствие

_i  P(_i)=P_i.

Возникает вопрос: как определить из конкретных условий решаемой задачи вероятность P(_i) отдельных элементарных исходов?

2.2 Классическое определения вероятности. Комбинаторика

Вычислять вероятности P(_i) можно, используя априорный подход, который заключается в анализе специфических условий данного эксперимента (до проведения самого эксперимента). Классическое определение вероятностей основано на понятии равновозможных событий.

Два или несколько событий называются равновозможными, если условия их появления одинаковы и нет оснований считать, что какое-либо из них имеет больше шансов появиться в результате опыта, чем другое.

Возможна ситуация, когда пространство элементарных исходов состоит из конечного числа N элементарных исходов, причем случайный эксперимент таков, что вероятности осуществления каждого из этих N элементарных исходов представляются равными.

Примеры таких случайных экспериментов: подбрасывание симметричной монеты, бросание правильной игральной кости, случайное извлечение игральной карты из перетасованной колоды. В силу введенной аксиомы вероятности каждого элементарного исхода в этом случае равны . Из этого следует, что если событие А содержит N_A элементарных исходов, то

.

В данном классе ситуаций вероятность события определяется как отношение числа благоприятных исходов к общему числу всех несовместных равновозможных исходов.

Чтобы пользоваться этим классическим определением вероятности, нужно уметь подсчитывать общее число исходов эксперимента и число благоприятных исходов. Такой подсчет сводится к перебору вариантов. Раздел математики, в котором исследуются различные задачи на перебор, называется комбинаторикой.

Элементы комбинаторики

Пусть имеется множество U_n, состоящее из n элементов.

Перестановкой из n элементов называется заданный порядок во множестве U_n:

Размещением из n элементов по k элементов будет называться любое упорядоченное подмножество, состоящее из k элементов множества U_n:

Сочетаниями из n элементов по k элементов называются подмножества, состоящее из k элементов множества U_n. Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).

Пример 9. В соревнованиях принимают участие 16 команд. Сколькими способами могут распределиться три первых места

Решение. Иными словами, необходимо найти число всех подмножеств, состоящих из трех элементов, отличающихся составом (номерами команд) или порядком их размещения. Таким образом, необходимо определить число размещений из 16 по 3