
- •Часть 1
- •1. Линейная алгебра
- •1.1. Основные классы квадратных матриц
- •Задачи для самостоятельного решения
- •1.2. Определители. Ранг матрицы
- •1.2.1. Вычисление определителей
- •1.2.2. Вычисление ранга матриц
- •Задачи для самостоятельного решения
- •1.3. Обратная матрица
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Как изменится матрица , если совершить аналогичные преобразования со столбцами матрицы а?
- •1.4. Жорданова нормальная форма
- •1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
- •Задачи для самостоятельного решения
- •1.6. Многочлены
- •Задачи для самостоятельного решения
- •2. Введение в анализ
- •2.1. Метод математической индукции
- •Алгоритм метода математической индукции
- •Решение. Используем метод математической индукции.
- •Задачи для самостоятельного решения
- •2.2. Пределы последовательностей
- •Упражнение 14. Найти
- •Примеры решения задач
- •Пример 2. Пусть , . Найти .
- •Задачи для самостоятельного решения
- •1. Вычислить пределы:
- •2.3. Предел функции. Непрерывность
- •Примеры решения задач
- •Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.
- •Задачи для самостоятельного решения
- •3.1. Производная функции. Вычисление производной по определению
- •Если он существует и конечен, называется правосторонней (левосторонней) производной и обозначается . Если существует производная , то будем говорить, что дифференцируема в точке .
- •Теорема 2. Если существует производная , то функция непрерывна в точке .
- •Примеры решения задач Пример 1. Пусть Подобрать коэффициенты a и b так, чтобы функция была дифференцируемой в точке .
- •Заметим, что как произведение бесконечно малой функции на ограниченную , после замены получим
- •Задачи для самостоятельного решения
- •1. Показать, что функция , где – непрерывная функция и , не имеет производной в точке .
- •2. Пусть
- •3.2. Вычисление пределов функций с использованием методов дифференциального исчисления
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1. Вычислить пределы
- •3.3. Выпуклые и вогнутые функции. Точки перегиба
- •Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
- •В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
- •Задачи для самостоятельного решения
- •3.4. Основные теоремы дифференциального исчисления
- •Примеры решения задач
- •Обратим внимание на то, что является точкой перегиба функции . Оказывается, что этот факт верен для любой дважды дифференцируемой функции.
- •Так как , то , что и требовалось доказать.
- •Задачи для самостоятельного решения
- •6. Исследование функции нескольких переменных на экстремум
- •7. Доказательство тождеств с использованием свойств дифференцирования
- •Задачи для самостоятельного решения
- •3.6. Производные высших порядков
- •Задачи для самостоятельного решения
- •Заключение
- •Часть 1
- •394006 Воронеж, ул. 20-летия Октября, 84
Примеры решения задач
Пример 1.
Вычислить
![]() для
для
 .
.
Решение. Обозначим
 .
.
Из
равенства
![]() и правила умножения матриц получаем
систему для нахождения
и правила умножения матриц получаем
систему для нахождения
![]() :
:

Вычитая
из второго уравнения третье, из третьего
– четвертое и, наконец, из (n–1)-го
уравнения n-е уравнение
получаем
![]() .
Теперь из первого уравнения получаем
.
Теперь из первого уравнения получаем
![]() ,
из второго –
,
из второго –
![]() .
.
Аналогично
вычисляем элементы матрицы, состоящие
в остальных столбцах, и получаем
![]() ,
если
,
если
![]() ,
,
![]() .
.
Таким образом,
 .
.
Пример 2. Вычислить для
 .
.
Решение.
Используем метод элементарных
преобразований. Проиллюстрируем этот
метод для матрицы порядка 4. Построим
матрицу
![]() размерности
размерности
![]() и преобразуем ее следующим образом: из
третьей строки вычтем четвертую и
результат запишем вместо третьей строки,
затем из второй получившуюся третью и
из первой получившуюся вторую. В итоге
получим матрицу
и преобразуем ее следующим образом: из
третьей строки вычтем четвертую и
результат запишем вместо третьей строки,
затем из второй получившуюся третью и
из первой получившуюся вторую. В итоге
получим матрицу
![]() ,
где
,
где
![]() .
.

 .
.
Таким
образом,
 .
.
Очевидно, что описанный метод безо всяких изменений применим в общем случае и дает следующий результат:
 .
.
Пример
3.
Доказать, что если матрица
![]() обратима, то матрица
обратима, то матрица
![]() также обратима.
также обратима.
Решение.
Первый
способ.
Предположим, что матрица
![]() необратима, тогда найдется вектор
необратима, тогда найдется вектор
![]() такой, что
такой, что
![]() .
В этом случае
.
В этом случае
![]()
Так
как
– обратимая матрица, то
![]() .
Отсюда получаем, что
.
Отсюда получаем, что
![]()
что противоречит нашему предположению.
Второй способ. Непосредственной проверкой убедиться, что
![]()
Пример
4. Найти
матрицу, обратную
 ,
где А
и С
–обратимые матрицы одного порядка.
,
где А
и С
–обратимые матрицы одного порядка.
Решение.
Первый
способ.
Иногда (в частности, и в этом случае)
бывает удобно начинать решение задачи
с рассмотрения простейшего частного
случая. Для начала будем считать, что
А,
В,
С
– матрицы первого порядка, то есть
обыкновенные числа, причем
![]() и
и
![]() .
Тогда
.
Тогда

При переходе к
общему случаю нужно обратить внимание
на выбор порядка множителей
![]() ,
так как умножение матриц, в отличие от
умножения чисел, – некоммутативная
операция. Путем несложного перебора
убеждаемся, что
,
так как умножение матриц, в отличие от
умножения чисел, – некоммутативная
операция. Путем несложного перебора
убеждаемся, что
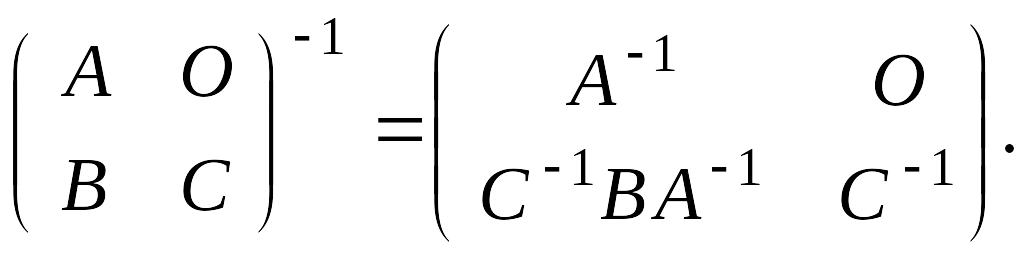 Действительно,
Действительно,

Второй
способ. Пусть
 – искомая матрица. Тогда
– искомая матрица. Тогда

Отсюда получаем четыре матричных уравнения
![]()
Так как А
обратима, то
![]() и
и
![]() .
.
Так как С
обратима, то
![]()
Таким образом,

Пример
5.
Пусть А – обратимая матрица
порядка n. Доказать,
что
![]() обратима
и
обратима
и
![]() .
.
Решение.
Возьмем два произвольных вектора
![]() и рассмотрим их скалярное произведение:
и рассмотрим их скалярное произведение:
![]() (согласно утверждению 2 раздела 1.1)
(согласно утверждению 2 раздела 1.1)
![]()
![]()
Отсюда следует, что
![]()
Так как x
– произвольный вектор, то можем
сделать подстановку
![]() ,
которая приводит к равенству
,
которая приводит к равенству
![]()
Так как модуль вектора равен нулю, только если этот вектор нулевой, то получаем равенство
![]()
Так как y –
произвольный вектор из
![]() то последнее равенство верно только в
случае, когда матрица
то последнее равенство верно только в
случае, когда матрица
![]() –
нулевая, то есть
–
нулевая, то есть
![]() .
По определению обратной матрицы это
означает, что
.
По определению обратной матрицы это
означает, что
![]() .
.
Задачи для самостоятельного решения
1.Найти обратные матрицы для следующих матриц:
а)
 б)
б)

в)
 г)
г)

2.
Найти матрицу
![]() из
уравнения
из
уравнения

3.
Найти обратную
матрицу для матрицы
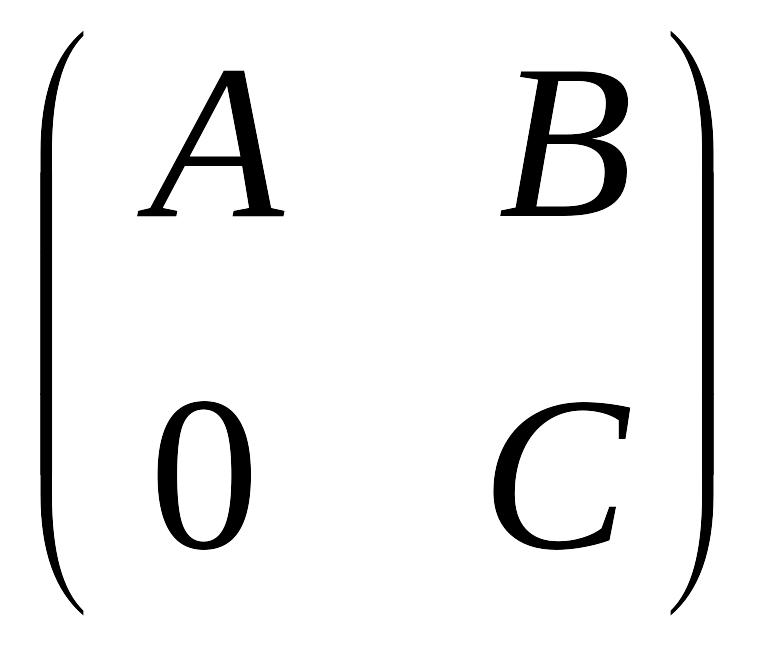 ,
где
,
где
![]() –
обратимые матрицы одного порядка.
Используя полученный результат, вычислить
–
обратимые матрицы одного порядка.
Используя полученный результат, вычислить

4.
Пусть
![]() –
обратимые матрицы одного порядка.
Показать, что равенства
–
обратимые матрицы одного порядка.
Показать, что равенства
![]()
равносильны.
5.
Пусть
![]() – матрицы
порядка
.
Доказать, что найдутся
– матрицы
порядка
.
Доказать, что найдутся
![]() чисел
чисел
![]() ,
не равные нулю одновременно, такие, что
матрица
,
не равные нулю одновременно, такие, что
матрица
![]() необратима.
необратима.
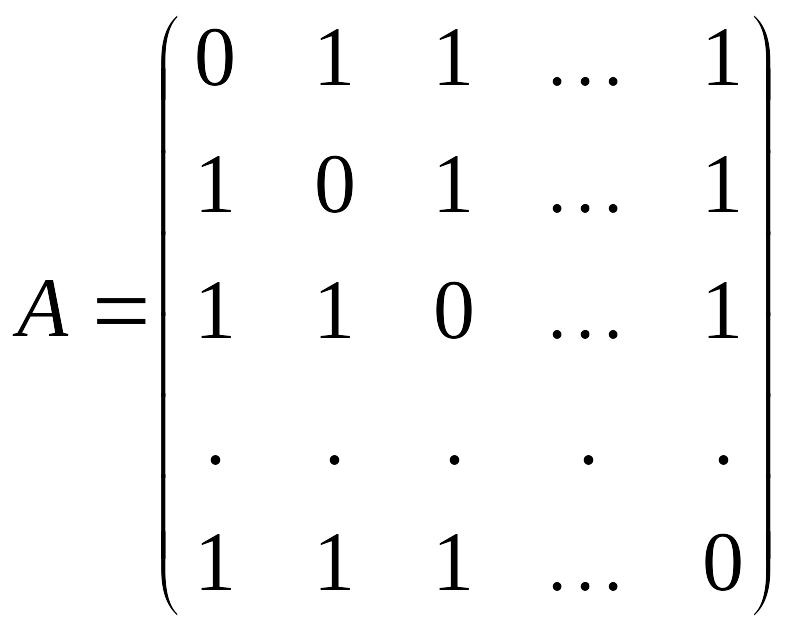
6. Пусть A – квадратная матрица порядка с нулями на главной диагонали и числами вне диагонали. Доказать, что при четных матрица А невырожденная, а при любом нечетном матрица А может быть и вырожденной и невырожденной. Привести соответствующие примеры.
7. Доказать, что если матрица А нильпотентная, то матрицы Е–А и Е+А обратимы.
8. Решить уравнение AX + X + A = 0, где А – заданная нильпотентная матрица.
9.
Указать, как изменится обратная матрица
![]() если в
матрице А:
если в
матрице А:
а) переставить i-ю и j–ю строки;
б) i-ю строку умножить на число с, не равное нулю;
в) к i-й строке прибавить j-ю, умноженную на число с.
