
- •Часть 1
- •1. Линейная алгебра
- •1.1. Основные классы квадратных матриц
- •Задачи для самостоятельного решения
- •1.2. Определители. Ранг матрицы
- •1.2.1. Вычисление определителей
- •1.2.2. Вычисление ранга матриц
- •Задачи для самостоятельного решения
- •1.3. Обратная матрица
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Как изменится матрица , если совершить аналогичные преобразования со столбцами матрицы а?
- •1.4. Жорданова нормальная форма
- •1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
- •Задачи для самостоятельного решения
- •1.6. Многочлены
- •Задачи для самостоятельного решения
- •2. Введение в анализ
- •2.1. Метод математической индукции
- •Алгоритм метода математической индукции
- •Решение. Используем метод математической индукции.
- •Задачи для самостоятельного решения
- •2.2. Пределы последовательностей
- •Упражнение 14. Найти
- •Примеры решения задач
- •Пример 2. Пусть , . Найти .
- •Задачи для самостоятельного решения
- •1. Вычислить пределы:
- •2.3. Предел функции. Непрерывность
- •Примеры решения задач
- •Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.
- •Задачи для самостоятельного решения
- •3.1. Производная функции. Вычисление производной по определению
- •Если он существует и конечен, называется правосторонней (левосторонней) производной и обозначается . Если существует производная , то будем говорить, что дифференцируема в точке .
- •Теорема 2. Если существует производная , то функция непрерывна в точке .
- •Примеры решения задач Пример 1. Пусть Подобрать коэффициенты a и b так, чтобы функция была дифференцируемой в точке .
- •Заметим, что как произведение бесконечно малой функции на ограниченную , после замены получим
- •Задачи для самостоятельного решения
- •1. Показать, что функция , где – непрерывная функция и , не имеет производной в точке .
- •2. Пусть
- •3.2. Вычисление пределов функций с использованием методов дифференциального исчисления
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1. Вычислить пределы
- •3.3. Выпуклые и вогнутые функции. Точки перегиба
- •Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
- •В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
- •Задачи для самостоятельного решения
- •3.4. Основные теоремы дифференциального исчисления
- •Примеры решения задач
- •Обратим внимание на то, что является точкой перегиба функции . Оказывается, что этот факт верен для любой дважды дифференцируемой функции.
- •Так как , то , что и требовалось доказать.
- •Задачи для самостоятельного решения
- •6. Исследование функции нескольких переменных на экстремум
- •7. Доказательство тождеств с использованием свойств дифференцирования
- •Задачи для самостоятельного решения
- •3.6. Производные высших порядков
- •Задачи для самостоятельного решения
- •Заключение
- •Часть 1
- •394006 Воронеж, ул. 20-летия Октября, 84
1.2. Определители. Ранг матрицы
1.2.1. Вычисление определителей
1. Метод приведения к треугольному виду
Этот метод основан на применении следующих двух теорем.
Теорема
1.
Определитель не меняется, если к элементам
одной из его строк (одному из его столбцов)
прибавить соответственные элементы
другой строки (другого столбца), умноженные
на некоторое число
![]() .
.
Теорема 2. Определитель верхней (нижней) треугольной матрицы равен произведению элементов главной диагонали.
Упражнение 1. Вычислить определитель
 .
.
Решение. Вычитаем первую строку из всех остальных и получаем:

2. Метод рекуррентных соотношений
Суть метода состоит в том, что исходный определитель разложением по строке или столбцу выражается через определители более низкого порядка, имеющие тот же вид.
Упражнение 2. Вычислить определитель
 .
.
Решение. Обозначим

Для
любого
![]() разложение определителя
разложение определителя
![]() по последнему столбцу приводит к
рекуррентному соотношению:
по последнему столбцу приводит к
рекуррентному соотношению:
![]() .
.
Непосредственные
вычисления показывают, что выполнены
равенства
![]()
![]()
![]() Предположим, что уже доказаны равенства
Предположим, что уже доказаны равенства
![]() для
для
![]() Разложим определитель
Разложим определитель
![]() по последнему столбцу и получим с учетом
сделанного предположения, что
по последнему столбцу и получим с учетом
сделанного предположения, что
![]()
Таким
образом, для любого
![]() верно равенство
верно равенство
![]() .
.
3. Метод разложения определителя на линейные множители
Метод
основан на возможности представления
произвольного многочлена
![]() степени
n
в виде
степени
n
в виде
![]() ,
где числа
,
где числа
![]() являются
корнями многочлена
.
являются
корнями многочлена
.
Предположим,
что требуется вычислить определитель
![]() ,
зависящий от параметра
,
причем известно, что
,
зависящий от параметра
,
причем известно, что
![]() является многочленом степени
от переменной
.
Если удается каким-либо образом установить
значения
является многочленом степени
от переменной
.
Если удается каким-либо образом установить
значения
![]() ,
при которых
,
при которых
![]() ,
то
,
то
![]() Чтобы найти
число аn
, нужно
любое число
Чтобы найти
число аn
, нужно
любое число
![]() ,
отличное от всех
,
отличное от всех
![]() ,
подставить вместо х
в исходный определитель и вычислить
его. Затем an
находится из равенства
,
подставить вместо х
в исходный определитель и вычислить
его. Затем an
находится из равенства
![]()
Упражнение 3. Вычислить определитель Вандермонда n – го порядка:

Решение.
Разложив определитель
![]() по последней строке, получим представление:
по последней строке, получим представление:
![]()
где
![]() –
алгебраическое дополнение элемента
–
алгебраическое дополнение элемента
![]() является определителем Вандермонда
порядка
является определителем Вандермонда
порядка
![]() ,
причем определители
не зависят от
,
причем определители
не зависят от
![]() .
Следовательно, определитель
является многочленом степени
переменной
:
.
Следовательно, определитель
является многочленом степени
переменной
:
![]() .
Заметим, что если
.
Заметим, что если
![]() ,
то i-я
строка совпадает с n-й
строкой. Следовательно,
,
то i-я
строка совпадает с n-й
строкой. Следовательно,
![]() для
для
![]() .
Таким образом,
.
Таким образом,
![]()
Аналогичным
образом получаем разложения для
![]() :
:
![]()
![]()
………………………………………………………
![]()
Окончательно получаем
![]()
![]()
то
есть
![]() – произведение всех множителей вида
– произведение всех множителей вида
![]() ,
где
,
где
![]() .
.
4. Применение теоремы Лапласа
Определение
1.
Пусть минор
![]() расположен на пересечении строк с
номерами
расположен на пересечении строк с
номерами
![]() и столбцов с номерами
и столбцов с номерами
![]() .
Дополнительным
минором
.
Дополнительным
минором
![]() минора
называется
минор, получающийся из
минора
называется
минор, получающийся из
![]() вычеркиванием строк
вычеркиванием строк
![]() и
столбцов
.
Алгебраическим
дополнением минора
называется
число
:
и
столбцов
.
Алгебраическим
дополнением минора
называется
число
:
![]()
Теорема
3. Пусть
в определителе
порядка
произвольно выбраны
![]() строк (или
столбцов).
Тогда сумма произведений всех миноров
строк (или
столбцов).
Тогда сумма произведений всех миноров
![]() го
порядка, содержащихся в выбранных
строках (столбцах),
на их алгебраические дополнения равна
определителю
.
го
порядка, содержащихся в выбранных
строках (столбцах),
на их алгебраические дополнения равна
определителю
.
Эта теорема обобщает правило разложения определителя по строке (столбцу).
Упражнение 4. Вычислить определитель
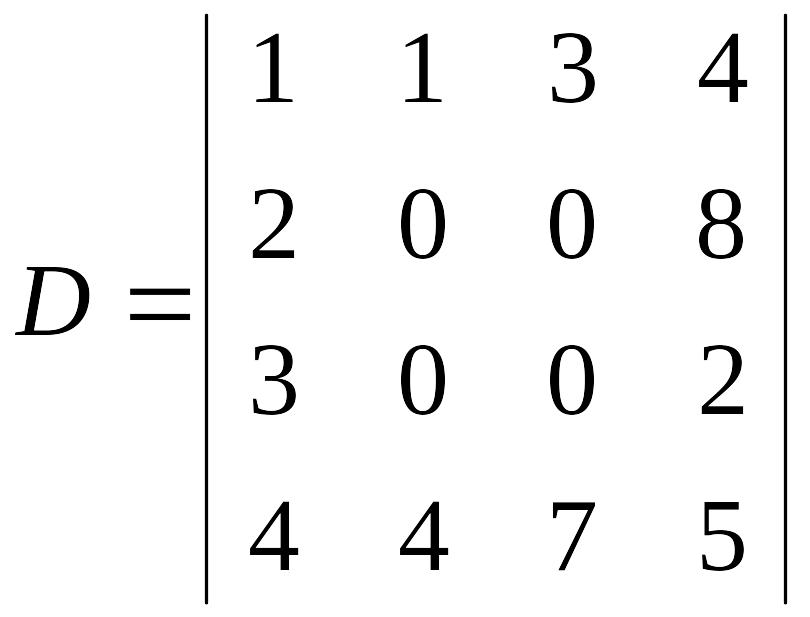 .
.
Решение. Зафиксируем 2-й и 3-й столбцы и в соответствии с теоремой Лапласа получим:



5. Использование теоремы о произведении определителей
Теорема
4. Определитель
произведения матриц равен произведению
их определителей:
![]() .
.
Эта теорема может быть применена различным образом в зависимости от того, вычисляем мы определитель произведения или определитель одного из множителей.
Упражнение 5. Вычислить определитель
 .
.
Решение.
Применим теорему 4, взяв
![]() и
и
![]() ,
и воспользуемся
свойством
,
и воспользуемся
свойством
![]() :
:
![]()

![]()
Следовательно,
![]() .
.
Заметим,
что использование равенства
![]() значительно менее эффективно для решения
этой задачи.
значительно менее эффективно для решения
этой задачи.
Упражнение 6. Вычислить определитель
 .
.
Решение. Из равенства

следует,
что
![]() ,
если
,
если
![]() , и
, и
![]() ,
если
,
если
![]() .
.
