
- •А. П. Бырдин, А. А. Сидоренко, О. А. Соколова
- •МАТЕМАТИКА
- •Практикум
- •А. П. Бырдин, А. А. Сидоренко, О. А. Соколова
- •Решение. Объем тела
- •Ответы
- •Формула
- •Задачи для самостоятельного решения
- •Ответы
- •Задачи для самостоятельного решения
- •Ответы
- •5.1. Понятие числового ряда
- •Суммы конечного числа членов ряда
- •Возьмем какой-нибудь знакопеременный ряд
- •Таким образом, при любом х имеет место разложение
- •Запишем разложение в ряд Маклорена других функций.
- •Задачи для самостоятельного решения
- •Ответы
- •6. СОБЫТИЕ И ВЕРОЯТНОСТЬ
- •Решение. Используя полученную в предыдущем примере таблицу, имеем
- •Задачи для самостоятельного решения
- •Ответы
- •Учебное издание
Решение. Здесь возможные значения для Xесть: х1 = 0,
х2 = 100, х3 = 10000, х4= 100000. Вероятности их будут:
р2 = 0.01, р3 = 0.001, р4 = 0.0001, р1 = 1 − 0.01 − 0.001 − 0.0001 = 0.9889. Следовательно, закон распределения выигрыша Xможет быть задан таблицей:
Х |
0 |
100 |
10000 |
100000 |
р |
0.9889 |
0.01 |
0.001 |
0.0001 |
Закон распределения полностью задает дискретную случайную величину. Однако часто встречаются случаи, когда закон распределения случайной величины неизвестен. В таких случаях случайную величину изучают по ее числовым характеристикам. Одной из таких характеристик является матема-
тическое ожидание.
Пусть некоторая дискретная случайная величина Xсконечным числом своих значений задана законом распределения:
X |
x1 |
x2 |
x3 |
… |
xn |
p |
p1 |
p2 |
p3 |
… |
pn |
Определение. Математическим ожиданием М(Х) дис-
кретной случайной величины Xназывают сумму произведений всех возможных значений величины X на соответствующие вероятности:
М(Х) = х1 р1 + х2 р2 + + хn pn . |
(6.10) |
Пример. Найти математическое ожидание выигрыша X в предыдущем примере.
Решение. Используя полученную в предыдущем примере таблицу, имеем
М(Х) = 0 0.9889+100 0.01+10000 0.001+100000 0.0001=
=1+10+10 = 21 р.
Очевидно, М(Х) = 21 р. есть справедливая цена одного лотерейного билета.
121
Теорема. Математическое ожидание дискретной случайной величиныX приближенно равно среднему арифметическому всех ее
значений(при достаточно большом числеиспытаний). |
|
|||||||||
|
Из статистического определения вероятности следует, |
|||||||||
что |
|
при |
достаточно |
большом |
числе |
испытаний |
||||
p* |
≈ p |
i |
(i =1, 2, , k).Поэтому х |
≈ х р |
+ х |
р |
+ + х |
p |
||
i |
|
|
|
ср. |
1 1 |
2 |
2 |
k |
k |
|
Или xср. ≈ М(Х).
Примечание. В связи с только что приведенной теоремой математическое ожидание случайной величины называют также ее средним значением, или ожидаемым значением.
Рассмотрим свойства математического ожидания дискретной случайной величины.
1. Математическое ожидание постоянной величины С равно этой величине.
Постоянную С можно рассматривать как дискретную случайную величину, принимающую лишь одно значение С с вероятностью р = 1. Поэтому М(С)= С 1= С.
2. Постоянный множитель можно выносить за знак математического ожидания, то есть М(СХ) = С М(Х).
3. Математическое ожидание суммы двух случайных величин X и Y равно сумме их математических ожиданий:
M (X +Y ) = M (X )+ M (Y ).
Определение. Случайные величины Xи Yназывают независимыми, если закон распределения каждой из них не зависит от того, какое возможное значение приняла другая величина.
Примером двух независимых случайных величин могут служить суммы выигрышей по каждому из двух билетов по двум различным денежно-вещевым лотереям. Здесь ставший известным размер выигрыша по билету одной лотереи не влияет на ожидаемый размер выигрыша и соответствующую ему вероятность по билету другой лотереи.
Несколько случайных величин называют независимыми, если закон распределения любой из них не зависит от того, ка-
122
кие возможные значения приняли остальные случайные величины.
4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M (XY ) = M (X ) M (Y ).
Следствием свойств 2 и 3 является свойство 5.
5. Математическое ожидание разности двух случайных величин Х и Y равно разности их математических ожиданий:
М(Х −Y) = M(X)−M(Y).
Примечание 1. Свойства 3 и 4 имеют место и для любого конечного числа случайных величин.
Примечание 2. Если множество возможных значений дискретной случайной величины X бесконечно, то математическое ожидание М(Х) определяется суммой число-
∞
вого ряда М(Х) = ∑ xk pk при условии, что этот ряд абсо- k =1
лютно сходится (в противном случае говорят, что матем а- тическое ожидание не существует). Перечисленные свойства математического ожидания остаются в силе и для таких случайных величин.
Пример. Найти математическое ожидание случайной величины Z = X + 2Y, если известны математические ожидания случайных величин X и Y: М(Х)= 5, M(Y) = 3.
Решение. Используя свойства 3 и 2 математического ожидания, получаем
М(Z) = M (X + 2Y ) = M (X )+ M (2Y ) =
=M (X )+ 2M (Y ) = 5+ 2 3 =11.
123
Пример. Независимые случайные величины заданы законами распределения
X |
1 |
2 |
P |
0.2 |
0.8 |
|
|
|
Y |
0.5 |
1 |
p |
0.3 |
0.7 |
Найти математическое ожидание случайной величиныXY. Решение. Найдем математические ожидания каждой из
данных величин:
М(Х) = 1 0.2 + 2 0.8= 1.8,
M(Y) = 0.5 0.3+1 0.7= 0.15 + 0.7 = 0.85.
Случайные величины X и Y независимы, поэтому искомое математическое ожидание
M(XY) = М(Х) М(Y ) =1.8 0.85= 1.53.
Математическое ожидание не дает полной характеристики закона распределения случайной величины.
Например, при одинаковой средней величине годовых осадков одна местность может быть засушливой и неблагоприятной для сельскохозяйственных работ (нет дождей весной и летом), а другая − благоприятной для ведения сельского хозяйства.
Из сказанного вытекает необходимость введения новой числовой характеристики случайной величины, по которой можно судить о «рассеянии»возможных значений этой случайной величины. Пусть задана дискретнаяслучайная величина X:
X |
|
x1 |
|
x2 |
|
… |
xn |
p |
|
p1 |
|
p2 |
|
… |
pn |
Определение. Отклонением случайной величины X от ее |
|||||||
математического |
ожидания |
M (X ) (или |
просто |
отклонением |
|||
124
случайной величины X) называют случайную величину
X − M (X ).
Видно, что для того, чтобы отклонение случайной величины X приняло значение x1−M (X ) , достаточно, чтобы слу-
чайная величина X приняла значение x1. Вероятность же этого события равна р1, следовательно, и вероятность того, что от-
клонение случайной величины Xпримет значение х1− M (X )
также равна р1.Аналогично обстоит дело и для остальных возможных значений отклонения случайной величины X. Используя это, запишем закон распределения отклонения случайной величины X:
Х−M (X ) |
x1 −M (X ) |
x2 −M (X ) |
… |
xn−M (X ) |
|
|
|
|
|
р |
р1 |
р2 |
… |
рn |
Вычислим теперь математическое ожидание отклонения Х −M (X ) .Пользуясь свойствами математического ожидания, получаем
М[Х −M (X ) ] = M (X ) −M (X ) = 0.
Следовательно, справедлива следующая теорема.
Теорема. Математическое ожидание отклонения X−M (X ) равно нулю: М[Х −M (X ) ] = 0.
Из теоремы видно, что с помощью отклонения X−M (X )
не удается определить среднее отклонение возможных значений величины Х от ее математического ожидания, то есть степень рассеяния величины X. Это объясняется взаимным погашением положительных и отрицательных возможных значений отклонения. Однако можно освободиться от этого недостатка, если рассматривать квадрат отклонения случайной величины X. Запишем закон распределения случайной величины [X−M (X ) ]2 (рассуждения те же, что и в случае случайной ве-
личины Х −M (X ) ).
125
[Х-М(Х)]2 |
[x1-M(X)]2 |
[x2-M(X)]2 |
… |
[xn-M(X)]2 |
р |
р1 |
р2 |
… |
рn |
Определение. Дисперсией D(X) дискретной случайной величины X называют математическое ожидание квадрата отклонения случайной величины Xот ее математического ожида-
ния: D(X ) = M[(X − M (X ))2].
Из закона распределения величины [Х −M (X ) ]2 следует,
что D(X ) = [x1 − M (X )]2 p1 +[x2 − M (X )]2 p2 + +
+[xn − M (X )]2 pn.
Свойства дисперсии дискретной случайной величины. 1. Дисперсия дискретной случайной величины X равна
разности между математическим ожиданием квадрата величины X и квадратом ее математического ожидания:
D(X) = M(X2 )−M2(X).
С помощью этого свойства и свойства математического ожидания устанавливаются следующие свойства.
2.Дисперсия постоянной величины С равна нулю.
3.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX) = C2D(X).
4.Дисперсия суммы двух независимых случайных величин
равна сумме дисперсий этих величин:D(X +Y ) = D(X )+ D(Y ).
Следствием свойств 3 и 4 является свойство 5.
5. Дисперсия разности двух независимых случайных вели-
чин X и Y равна сумме их дисперсий:D(X−Y) = D(X)+D(Y).
Пример. Дисперсия случайной величины X равна 3.
Найти дисперсию следующих величин: а) −3Х; б) 4Х + 3. Решение.Согласно свойствам 2, 3 и 4 дисперсии имеем
а)D(−3X ) = 9D(X ) = 9 3 = 27 ;
б) D(4X + 3) = D(4X) + D(3) = 16D(X)+ 0 =16 3 = 48.
Определение. Средним квадратическим отклонением
126

s (X) случайной величины X называется корень квадратный из ее дисперсии: s(X ) = 
 D(X ).
D(X ).
Введение среднего квадратического отклонения объясняется тем, что дисперсия измеряется в квадратных единицах относительно размерности самой случайной величины. Например, если возможные значения некоторой случайной величины измеряются в метрах, то ее дисперсия измеряется в квадратных метрах. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, и используется среднее квадратическое отклонение.
Пример. Случайная величина X − число очков, выпавших при однократном бросании игральнойкости. Определить s(X ).
Решение. Имеем
M (X ) =1 16 + 2 16 +3 16 + 4 16 +5 16 +6 16 = 3.5;
D(X ) = (1 −3.5)2 16 + (2−3.5)2 16 + (3−3.5)2 16 +
+ (4 |
−3.5) |
2 |
|
1 |
+ (5 |
−3.5) |
2 |
|
1 |
+ (6 |
−3.5) |
2 |
|
1 |
= |
35 |
; |
|
6 |
|
6 |
|
6 |
12 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
s(X ) = |
|
35 |
≈1.71. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
6.6.2. Непрерывные случайные величины
Для непрерывной случайной величины в отличие от дискретной нельзя построить таблицу распределения. Поэтому непрерывные случайные величины изучают другим способом. Пусть X−непрерывная случайная величина с возможными значениями из некоторого интервала (а; b) и х −действительное число. Под выражением X < x понимается событие «случайная величина X приняла значение, меньшее х». Вероятность
127

этого события P(X < x)есть некоторая функция переменной х:
F(x) = P(X < x).
Определение. Интегральной функцией распределения
(или кратко функцией распределения)непрерывной случайной величины Xназывается функция F(x),равная вероятности того, что Xприняла значение, меньшее х:
F(x) = P(X < x). |
(6.11) |
Отметим, что функция распределения совершенно также определяется для дискретных случайных величин.
Укажем свойства, которыми обладает функция F(x). 1. 0 ≤ F(x) ≤1.
2.F(x) − неубывающая функция, то есть, если х1< х2 , то
F(x1)≤F(x2).
3. Вероятность попадания случайной величины X в полуинтервал [а;b) равна разности между значениями функции распределения в правом и левом концах интервала (а; b):
P(a ≤ X < b) = F(b)− F(a). |
(6.12) |
|||||
Пример. Случайная величина X задана функцией рас- |
||||||
пределения: |
|
|
|
|
|
|
|
|
|
0 |
при |
x ≤ −1; |
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
||
F(x) = |
|
+ |
|
при |
−1< x ≤ 3; |
|
4 |
4 |
|
||||
|
|
при |
x > 3. |
|
||
|
|
|
1 |
|
||
|
|
|
|
|
|
|
Найти вероятности того, что в результате испытания X примет значение, принадлежащее полуинтервалу [0;2).
Решение.Так как на полуинтервале [0;2) F(x) = 4x + 14 , то
P(0 ≤ X < 2) = F(2)− F(0) = 12 + 14 − 14 = 12.
128
В дальнейшем случайную величину X будем называть непрерывной, если непрерывна ее функция распределения F(x).
4. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:
P(X = x1) = 0. |
(6.13) |
5. Вероятности попадания непрерывной случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы
P(a < X < b) = P(a ≤ X ≤ b) = P(a ≤ X < b) = P(a < X ≤ b).
6. Если возможные значения случайной величины X принадлежат интервалу (а;b), то 1) F(x) = 0 при х ≤ а;
2) F(x) = 1 при х ≥ b.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то спра-
ведливы следующие предельные соотношения: |
|
||
F(−∞) = lim |
F(x) = 0; |
F(+∞) = lim |
F(x) =1. |
x→−∞ |
|
x→+∞ |
|
Дифференциальной функцией распределения непрерыв-
ной случайной величины X (или ее плотностью вероятности) называется функция f (x), равная производной интегральной
функции: f (x) = F ′(x).
Так как F(x) − неубывающая функция, то f (x) ≥ 0.
Теорема. Вероятность попадания непрерывной случайной величины X в интервал (а;b) равна определенному интегралу от дифференциальной функции распределения величины
X, взятому в пределах от а до b:
b
P(a < X < b) = ∫
a
f (x)dx. (6.14)
Из (6.14) следует, что геометрически вероятность P(a < X < b)представляет собой площадь криволинейной тра-
пеции, ограниченной графиком |
плотности вероятности |
y = f (x)и отрезками прямых у = 0, |
x = a и x = b . |
129

Следствие. В частности, если f (x)− четная функция и концы интервала симметричны относительно начала коорди-
a
нат, то P(−a < X < a) = P( X < a) = 2∫f (x)dx.
0
Пример. Продолжительность жизни растений данного вида в определенной среде представляет собой непрерывную случайную величину X. Пусть функцией плотности вероятно-
сти для X является f (x) = 1201 e−120x . Какая доля растений данного вида умирает за период 100 дней?
Решение. По свойству 5, согласно формуле(6.14)
|
100 |
|
|
1 |
|
− |
x |
|
− |
x |
|
|
100 |
−5 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
P(0 ≤ X ≤100) |
= ∫ |
|
|
|
e |
|
120dx = −e |
120 |
|
|
=1 −e |
6 ≈ 0.7. |
|||
120 |
|
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
||||
В силу приведенного выше, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||
|
F(x) = |
∫ f (x)dx. |
|
|
|
|
|
(6.15) |
|||||||
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
||
Формула (6.15) дает возможность отыскать интегральную |
|||||||||||||||
функцию распределенияF(x)по ее плотности вероятности. |
|||||||||||||||
Отметим, что из формулы (6.15) и из только что отм е- |
|||||||||||||||
ченного следствия вытекает, что |
|
|
|
|
|
|
|||||||||
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∫ |
f (x)dx =1. |
|
|
|
|
|
(6.16) |
||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
||
Пример. Задана плотность вероятности случайной вели- |
|||||||||||||||
чины X f (x) = |
A |
|
|
(−∞ < x < +∞).Требуется найти коэф- |
|||||||||||
1 + x2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
фициент А,функцию распределения F(x) и вероятность попадания случайной величины Х в интервал (0; 1).
Решение. Коэффициент А найдем, воспользовавшись соотношением (6.16). Так как
130

+∞ |
f (x)dx = |
+∞ |
Adx |
= |
0 |
Adx |
+ |
+∞ |
|
|
Adx |
= |
∫ |
∫ |
|
∫ |
|
∫ |
|
|
|
||||
|
|
1 |
+ x2 |
|||||||||
−∞ |
|
−∞1 + x2 |
|
−∞1 + x2 |
|
0 |
|
|||||
=Aarctg x 0−∞ + Aarctg x 0+∞ = A[arctg(+∞)−
−arctg(−∞)] = Aπ,
то Aπ =1 , откуда A = π1 .
Применяя формулу (6.15), получаем функцию распределения F(x):
F(x) = |
x |
dx |
|
|
1 |
arctg x |
|
x |
|
|
|
||||||
∫ |
= |
|
|
= |
||||
|
−∞π(1+ x2) |
|
π |
|
−∞ |
|||
= π1 [arctg x − arctg(−∞)] = 12 + π1 arctg x.
Наконец, формулы (6.11) и ( 6.13) с учетом найденной функции F(x) даютP(0 < X <1) = F(1)− F(0) = 14 .
Определение. Математическим ожиданием непрерывной случайной величины X с плотностью вероятности f (x) называют
величинунесобственного интеграла (если он сходится):
+∞
M (X ) = ∫ x f (x)dx.
−∞
Определение. непрерывной случайной величины X, мате-
матическое ожидание которой М(Х) = а и функция f (x)явля-
ется ее плотностью вероятности, называется величина несобственного интеграла (если он сходится):
D(X ) = +∞∫ (x − a)2 f (x)dx.
−∞
Можно показать, что математическое ожидание и дисперсия непрерывной случайной величины имеют те же свойства, что и математическое ожидание и дисперсия дискретной случайной величины.
131

Для непрерывной случайной величины X среднее квадратическое отклонение s (Х) определяется, как и для дискретной
величины, формулой s(X ) = 
 D(X ) .
D(X ) .
Пример. Случайная величина X задана плотностью вероятности
0 |
при |
x < 0, |
|
|
|
|
|
f (x) = |
x |
при |
0 ≤ x ≤ 2, |
|
|||
2 |
при |
x > 2. |
|
0 |
|||
|
|
|
|
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины X.
Решение.Согласно определениям
|
|
+∞ |
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
x3 |
|
2 |
|
4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
M (X ) = |
∫ |
x f (x)dx = |
|
∫ x |
|
|
dx = |
|
|
|
|
|
|
= |
|
, |
|||||||||
2 |
|
|
6 |
|
|
|
3 |
||||||||||||||||||
|
|
−∞ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
||||||
D(X ) = |
+∞ |
|
|
4 |
|
2 |
f (x)dx = |
2 |
|
|
4 2 |
1 |
x dx = |
||||||||||||
∫ x − |
3 |
|
|
∫ |
x − |
3 |
|
2 |
|||||||||||||||||
|
−∞ |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||
|
= |
1 |
2 |
|
|
|
− |
8 |
x2 |
+ |
16 |
x |
|
= |
2 |
|
|
|
|
||||||
|
2 |
∫ |
x3 |
3 |
9 |
|
dx |
9 |
|
|
|
|
|
||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и, наконец, s(X ) = 
 D(X ) =
D(X ) =  32 ≈ 0.47.
32 ≈ 0.47.
6.7. Некоторые законы распределения случайных величин
6.7.1. Биномиальное распределение
Пусть производится п испытаний, причем вероятность появления события А в каждом испытании равна р и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события А в одном испыта-
нии равна р, то вероятность его ненаступления равна q = 1−р.
132

Найдем вероятность того, что приn испытаниях событие А наступит т раз (т ≤ п).
Пусть событие А наступило в первых т испытаниях т раз и не наступило во всех последующих испытаниях. Это сложное событие можно записать в виде произведения:
AA...A AA...A.
mраз n−m раз
Общее число сложных событий, в которых событие А наступает т раз, равно числу сочетаний из п элементов по т элементов. При этом вероятность каждого сложного события равна: pmqn-m.Так как эти сложные события являются несовместимыми, то вероятность их суммы равна сумме их вероятно-
стей. Итак, если Pn (m) есть вероятность появления события А
т раз в п испытаниях, тоP |
(m) = C m pmqn−m или |
|
||||
|
|
n |
n! |
n |
|
|
P |
(m) = |
|
pmqn−m . |
(6.17) |
||
|
|
|
||||
n |
|
m!(n − m)! |
|
|
||
|
|
|
|
|||
Формулу (6.17) называют формулой Бернулли.
Пример. Пусть всхожесть семян данного растения составляет 90 %. Найти вероятность того, что из четырех посеянных семян взойдут: а) три; б) не менее трех.
Решение. а) В данном случае n = 4, т = 3, р = 0.9, q = 1−p = 0.1.Применим формулуБернулли (6.17):
P4 (3) = 3!1!4! (0.9)3 0.1= 0.2916.
б) Здесь событие А состоит в том, что из четырех семян взойдут или три, или четыре. По теореме сложения вероятно-
стейP(A) = P4 (3)+ P4 (4). Но Р4(4)= (0.9)4= 0 .6561. Поэтому
Р(А) = 0.2916 + 0.6561 = 0.9477.
Снова рассмотрим n независимых испытаний, в каждом из которых наступает событие А с вероятностью р. Обозначим
133

через X случайную величину, равную числу появлений события А в п испытаниях.
Понятно, что событие А может вообще не наступить, наступить один раз, два раза и так далее, и наконец, наступить п раз. Следовательно, возможными значениями величины X
будут числа 0, 1, 2, ..., n− 1, п. По формуле Бернулли можно найти вероятности этих значений:
|
|
|
P |
(0) |
= C 0qn |
= qn , |
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
P |
(1) |
= C1 qn−1 p, |
|
|
||
|
|
|
n |
|
n |
|
|
|
|
|
|
|
.............................. |
|
|
||||
|
|
|
P |
(n) = pn . |
|
|
|
||
|
|
|
n |
|
|
|
|
|
|
|
Запишем полученные данные в виде таблицы распреде- |
||||||||
ления: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
X |
|
0 |
1 |
… |
|
m |
… |
n |
|
p |
|
qn |
С1n pqn−1 |
… |
Cnm pm qn−m |
… |
pn |
||
Построенный закон распределения дискретной случай-
ной величины X называют законом биномиального распределе-
ния. Математическое ожидание такой случайной величины М(Х) = пр, дисперсия D(Х) = прq, среднее квадратическое от-
клонение s(X ) = 
 npq.
npq.
Пример. Случайная величина X определена как число выпавших гербов в результате 100 бросаний монеты. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение X.
Решение. Вероятность появления герба в каждом бросании монеты p = 12. Следовательно, вероятность не появления
134

герба q =1 − 12 = 12 .Случайная величина X имеет биномиальное
распределение при п = 100 и p = 12.Поэтому
M (X ) = np =100 12 = 50, D(X ) = npq =100 12 12 = 25,
s(X ) = 
 npq =
npq = 
 25 = 5.
25 = 5.
Пример. Допустим, что для хищника вероятность поимки отдельной жертвы составляет 0,4 при каждом столкновении с жертвой. Каково ожидаемое число пойманных жертв в 20 столкновениях?
Решение. Это пример биномиального распределения при п = 20 и р= 0.4. Ожидаемое число есть М(Х)= пр =20 0.4 = 8.
6.7.2. Локальная и интегральная предельные теоремы Лапласа
Если число испытаний п велико, то вычисления по формуле Бернулли становятся затруднительными. Лаплас получил важную приближенную формулу для вероятностиРn(т)появления события Аточно m раз, если пдостаточно большое число.
Локальная предельная теорема Лапласа. Пусть p = P(A) − вероятность события А, причем 0 < p <1. Тогда
вероятность того, что в условиях схемы Бернулли событие А при п испытаниях появится точно т раз, выражается приближенной формулой Лапласа
Pn (m) ≈
где q =1 − p, ϕ(x) =
1

 npq
npq
1

 2π
2π
ϕ m − np ,
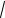 npq
npq
− x 2
e 2 .
Дляфункцииϕ(x)имеетсятаблица ( прил.1) еезначенийдляположительныхзначенийх(функция
(6.18)
ϕ(x)четная).
135

Пример. Вероятность поражения цели стрелком при одиночном выстреле равна р = 0.2. Какова вероятность того, что при 100 выстрелах цель будет поражена ровно 20 раз?
Решение. Здесь р = 0 .2, q= 0.8, n = 100 и т = 20. Отсюда
|
|
= |
|
|
|
|
= 4 и, |
следовательно,t = m −np |
= 20−100 0.2 =0. |
|||||||||||
|
npq |
100 0.2 0.8 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
|
4 |
|
|
Учитывая, |
что |
ϕ(0) = |
|
1 |
|
≈ 0.40, из формулы (6.18) |
||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
2π |
||||||||||||||||||
|
|
|
|
|
(20) ≈ 0.40 1 |
|
|
|
|
|
|
|
||||||||
получаемP |
= 0.10 (для получения приближен- |
|||||||||||||||||||
|
|
|
100 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
ного |
равенства |
|
|
≈ 0.40 можноиспользовать калькулятор). |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
2π |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Перейдем к интегральной предельной теореме Лапласа.
Поставим следующий вопрос. Какова вероятность того, что в условияхсхемы Бернулли событие А,имеющее вероятность P(A) = p (0 < p <1), при п испытаниях (как и прежде, число
испытаний велико) появится не менее kраз и не более l раз. Эту искомую вероятность обозначим через Pn(k, l).
|
xl |
|
|
|
|
|
1 |
|
|
|
xl |
2 |
|
|
||||||||
P (k,l) |
≈ ∫ ϕ(x)dx |
= |
|
|
|
|
∫ e−x |
|
/ 2dx, |
(6.19) |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|||||||||||||||||||
n |
xk |
|
|
|
|
|
|
2π xk |
|
|
|
|||||||||||
где |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
k |
− np |
|
|
|
|
|
|
|
|
|
l |
− np |
|
|
|
|
|
||||
xk |
= |
|
|
, |
|
|
xl |
= |
|
. |
|
|
(6.20) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
npq |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
|
|
|
||||||
Это составляет содержание интегральной предельной |
||||||||||||||||||||||
теоремы Лапласа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Введем функцию |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Ф(x) = |
|
|
|
|
∫e−t 2 / 2dt, |
|
|
(6.21) |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
2π |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
называемую функцией Лапласа или интегралом вероятно-
стей. Очевидно, Ф(х) есть первообразная для функции ϕ (х). Так как ϕ (х) > 0 в (− ∞, + ∞), то Ф(х) − возрастающая функ-
136

ция в этом интервале. На основании формулы НьютонаЛейбница из формулы (6.19) получаем
Pn (k,l) ≈ Ф(xl )−Ф(xk ). |
(6.22) |
|||||
Это − интегральная формула Лапласа. |
|
|||||
Как известно, интеграл |
|
1 |
|
∫e−x2 / 2dx не берется в эле- |
||
|
|
|
||||
2π |
||||||
|
|
|
|
|
||
ментарных функциях. Поэтому для функции (6.21) составлена таблица ее значений для положительных значений х (прил. 2), так как Ф(0) = 0 и функция Ф(x) нечетная,
|
|
1 |
|
−х |
|
|
1 |
|
x |
|
Ф(−х) = |
|
|
∫ |
е−t 2 / 2dt = − |
|
|
∫e−z 2 / 2dz = −Ф(х) |
|||
|
|
|
|
|
|
|||||
2π |
2π |
|||||||||
|
|
0 |
|
|
0 |
|||||
(t = −z, dt = −dz).
Пример. Вероятность того, что изделие не прошло проверку ОТК, равна 0.2. Найти вероятность того, что среди 400 случайно отобранных изделий окажутся непроверенными от 70 до 100 изделий.
Решение. Здесь n = 400 , k = 70 , l =100 , |
p = 0.2, |
q = 0.8. Поэтому, в силу равенств ( 6.20) xk = −1.25, x1 |
= 2.5 и |
согласно формуле (6.22),
P400(70, 100) = Ф(2.5) −Ф(−1.25) = Ф(2.5) + Ф(1.25) = = 0.4938 + 0.3944 = 0.8882.
6.7.3. Распределение Пуассона
Пусть производится серия п независимых испытаний (п = 1, 2, 3, ...), причем вероятность появления данного собы-
тия А в этой серии P(A) = pn > 0 зависит от ее номера п и
стремится к нулю при п →∞ (последовательность «редких событий»).Предположим, что для каждой серии среднее значе-
ние числа появлений события А постоянно, то есть прn = µ = =const. Отсюда pn = µn .
137
Исходя из формулы Бернулли (6.17), для вероятности появления события А в n-й серии ровно т раз имеем выражение
P (m) |
= C m pm (1 − p |
|
)n |
−m |
|
|
µ m |
− |
µ n−m |
|
||||||||||||||
n |
= C m |
|
1 |
. |
|
|||||||||||||||||||
n |
|
|
n n |
|
|
|
|
|
|
|
|
n |
n |
|
|
n |
|
|
|
|||||
Пусть т фиксировано. Тогда |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
lim |
m |
|
µ m |
= |
|
lim |
n(n |
−1)(n − 2) (n − (m |
−1)) |
µ |
m |
= |
||||||||||||
Cn |
|
|
|
|
|
|
|
|
|
m!nm |
|
|
|
|
|
|||||||||
n→∞ |
µm |
n |
|
n→∞ |
|
|
|
|
|
|
|
|
µm |
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
m − |
1 |
|
|
|
|
||||||
= |
|
|
lim 1 1 |
− |
|
1 − |
|
|
1 − |
|
|
|
= |
|
; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
m! |
|
|
|
|
|
n |
|
|
n |
|
|
|
n |
|
|
|
m! |
|
|
|
|||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
lim |
|
− |
µ n−m |
|
= e |
−µ |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
n→∞ |
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||
(здесь использован второй замечательный предел).
Поэтому |
lim P (m) = |
µm e−µ. |
|
|
|
|
n→∞ n |
m! |
|
|
|
Если п велико, |
то в силу определения предела, вероят- |
||||
ность Рп |
(т)сколь угодно мало отличается от |
µm |
e−µ . Отсюда |
||
m! |
|||||
|
|
|
|
||
при больших п для искомой вероятности Рn(т)имеем приближенную формулу Пуассона (для простоты знак приближенного равенства опущен)
|
P (m) = µm e−µ , |
где |
µ |
= np . |
|
|
|
|
||||
|
|
n |
m! |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определение. Говорят, что случайная величина X распреде- |
||||||||||||
лена позакону Пуассона, если эта величина задана таблицей: |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
0 |
|
1 |
|
2 |
|
|
3 |
|
|
… |
|
|
e−µ |
|
µe−µ |
|
µ2 |
−µ |
|
µ3 |
−µ |
|
|
|
P |
|
|
2! e |
|
|
3! e |
|
|
… |
|
||
138

Здесь µ − фиксированное положительное число (разным значениям µ отвечают разные распределения Пуассона).
Найдем математическое ожидание дискретной величины X, распределенной по закону Пуассона. Согласно определению математического ожидания
|
∞ |
µk |
|
−µ |
|
|
−µ |
∞ |
µk −1 |
|
|
−µ |
|
|
µ |
|||
M (X ) = |
∑ k |
|
e |
|
|
|
= µe |
|
∑ |
|
|
= µe |
|
e |
|
|||
k! |
|
|
|
|
(k −1)! |
|
|
|||||||||||
|
k =0 |
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|||
Найдем далее D(X).Сначала найдем М(Х 2): |
|
|
|
|||||||||||||||
M (X 2) = |
∞ |
|
2 |
µk |
|
|
|
∞ |
|
µk −1 |
|
|
|
|||||
∑ |
k |
|
|
|
e−µ = µe−µ ∑ k |
|
|
|
= |
|||||||||
|
|
k! |
(k −1)! |
|||||||||||||||
|
|
k =0 |
|
|
|
|
|
|
|
k =1 |
|
|
|
|||||
|
∞ |
µk −2 |
|
|
|
|
|
|
|
|
+ eµ ) = µ2 |
|||||||
= µe−µ |
µ ∑ |
|
|
|
|
+ eµ |
= |
µe−µ (µeµ |
||||||||||
|
|
|
|
|||||||||||||||
|
k =2 |
(k − 2)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теперь по известной формуле
D(X ) = M (X 2)− M 2(X ) = µ2 + µ − µ2 = µ.
=µ.
+µ.
Пример (радиоактивный распад). Рассмотрим пробу ра-
диоактивного вещества, которое в среднем дает r импульсов радиоактивности в одну секунду. Ожидаемое число импульсов за t секунд есть rt. Этот процесс можно описать распределением Пуассона. Проба состоит из очень большого числа п радиоактивных атомов, причем каждый атом имеет крайне малую вероятность р распада в течение одной секунды. Ожидаемое число распадов за 1 секунду есть r = пр . Ожидаемое число распадов за t секунд есть rt = npt. Это является математическим ожиданием распределения Пуассона, которое дает вероятность k распадов за t секунд:
P(k) = (rtk)!k e−rt .
Если, например, имеется три импульса радиоактивности в 1 секунду, то вероятность возникновения 10 импульсов за
139

5-секундный интервал составляет
P(10) = (3 5)10 e−35 = 1510 e−15. 10! 10!
6.7.4. Равномерное распределение
Распределение вероятностей непрерывной случайной величины X, принимающей все свои значения из отрезка [а; b], называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю, то есть
|
0 |
при |
x < a, |
|
f (x) |
|
при |
a ≤ x ≤ b, |
|
= c |
|
|||
|
|
при |
x > b. |
|
Отсюда |
0 |
|
||
|
|
b |
|
|
+∞ |
|
|
||
∫ f (x)dx = ∫c dx = c(b −a). |
(6.23) |
|||
|
||||
−∞ |
|
a |
|
|
Но, как известно,+∞∫ f (x)dx =1. Из сравнения этого равен-
−∞
ства с (6.23) получаем c = b −1 a .
Плотность вероятности, математическое ожидание и дисперсия непрерывной случайной величины X, распределенной равномерно на отрезке [а;b], имеет вид
|
0 |
|
при x < a, |
|
|||
|
|
1 |
|
|
|
||
|
|
|
|
|
|||
f (x) = |
|
|
при a ≤ x ≤ b, |
||||
|
|
||||||
|
b − a |
при x > b. |
|
||||
|
0 |
|
|
||||
|
|
|
|
|
|
||
M (X ) = |
a + b |
|
и D(X ) = |
1 |
(a − b)2. |
||
|
|
|
|
||||
2 |
|
|
|
12 |
|
||
140

Пример. На отрезке [а;b]наугад указывают точку. Какова вероятность того, что эта точка окажется в левой половине отрезка?
Решение. Пусть X-случайная величина, равная координате выбранной точки. X распределена равномерно (в этом и состоит точный смысл слов: «наугад указывают точку»), а так
как середина отрезка [а;b] имеет координату a +2 b , то искомая вероятность равна
|
a + b |
|
(a+b)/ 2 |
|
|
(a+b)/ 21 |
|
|||||
P a < X < |
|
|
= |
|
|
f (x)dx = |
|
|
|
dx = |
||
2 |
|
∫ |
|
∫b − a |
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
1 |
|
a + b |
|
|
1 |
|
|
|
||
|
= |
|
|
|
2 |
|
− a |
= |
2 |
. |
|
|
|
|
|
|
|
|
|||||||
|
|
b − a |
|
|
|
|
|
|
||||
6.7.5. Закон нормального распределения. Центральная
предельная теорема
Закон распределения вероятностей непрерывной случайной величины X называется нормальным, если ее диф-
ференциальная функция |
f (x)определяется формулой |
|
|||||
|
|
1 |
|
e− |
(x−a)2 |
|
|
f (x) = |
|
|
2s 2 , |
(6.24) |
|||
|
|
|
|
||||
s |
|
2π |
|||||
|
|
|
|
|
|
||
где параметр а совпадает с математическим ожиданием величины X:a = M (X ),параметр s является средним квадра-
тическим отклонением величины X :s =s(X ).
График функции (6.24) будет иметь вид, как на рис. 31. Причем его максимальная ордината равна 1/(s 
 2π ).
2π ).
Значит, эта ордината убывает с возрастанием значения s (кривая «сжимается» к оси Ох) и возрастает с убыванием
141

значения s «растягивается» в положительном направлении оси Оу), что отражено на рис. 32. Изменение значений параметра а (при неизменном значении s ) не влияет на форму кривой.
f(x)
0 |
|
|
|
a |
xx |
||
|
|
|
|
Рис. 31
Нормальное распределение с параметрамиa = 0 и s = 1 называют нормированным. Дифференциальная функция в слу-
чае такого распределения |
ϕ(x) = |
|
1 |
|
e |
−x2 |
/2 |
. |
|
|
|
|
|
||||
2π |
|
|
||||||
|
|
|
|
|
|
|
|
y
s1
s1 <s2 <s3
s2
s3
0 |
a |
x |
|
Рис. 32
Рис.
142

Пусть случайная величина Xраспределена по нормальному закону. Тогда вероятность того, что Xпримет значение, принадлежащее интервалу (α; β ),
|
|
1 |
|
β |
− |
(x−a)2 |
|
P(α < X < β) = |
|
|
∫e |
2s 2 dx. |
|||
s |
|
|
|
|
|||
2π |
|
||||||
|
|
|
|
|
α |
|
|
Вычислив этот интеграл, имеем
|
β − a |
|
α − a |
(6.25) |
|||
P(α < X < β) = Ф |
|
|
−Ф |
|
. |
||
s |
s |
||||||
|
|
|
|
|
|||
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Xот ее математического ожидания по абсолютной величине меньше заданного положительного числа δ , то есть найти
P( |
|
|
X − a |
|
< δ). Используя формулу (6.25) |
и нечетность функ- |
||||||||||||
|
|
|
||||||||||||||||
ции Ф(х), имеем |
|
δ |
|
δ |
|
δ |
||||||||||||
P( |
|
|
X − a |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
< δ) = P(a −δ < X < a +δ) = Ф |
|
−Ф − |
|
= 2Ф |
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
s |
s |
|||
то есть |
||||||||||||||||||
δ |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
P( |
|
X − a |
|
|
|
|
|
(6.26) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
< δ) = 2Ф |
.…………... |
||||||||
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Пусть случайная величина Х распределена по нормальному закону с параметрами а = 20 и s = 10. Найти
P( X − 20 < 3).
Решение.Используя формулу (6.26), имеем
|
|
|
3 |
|
|||
|
|
|
|||||
P( |
X − 20 |
< 3) |
= 2Ф |
|
|
. |
|
10 |
|||||||
|
|
|
|
|
|||
|
|
|
|||||
По таблице (прил. 2) находим Ф(0.3) = 0 .1179. Поэтому
P( X − 20 < 3)= 0.2358.
143

6.7.6. Распределение случайных ошибок измерения
Пусть производится измерение некоторой величины. Разность х − а между результатом измерения х и истинным значением а измеряемой величины называется ошибкой измерения. Вследствие воздействия на измерение большого числа факторов, которые невозможно учесть (случайные изменения температуры, колебание прибора, ошибки, возникающие при округлении, и т.п.), ошибку измерения можно считать суммой большого числа независимых случайных величин, которая по центральной предельной теореме должна быть распределена нормально. Если при этом нет систематически действующих факторов (например, неисправности приборов, завышающих при каждом измерении показания приборов), приводящих к систематическим ошибкам, то математическое ожидание случайных ошибок равно нулю.
Итак, принимается положение: при отсутствии систематически действующих факторов ошибка измерения есть случайная величина (обозначим ее через Т), распределенная нормально, причем ее математическое ожидание равно нулю, то
|
|
1 |
|
e− |
t2 |
||
есть плотность вероятности величины Т равна |
|
|
2s 2 |
, |
|||
|
|
|
|
||||
s |
|
2π |
|||||
|
|
|
|
|
|
||
где s − среднеквадратическое отклонение величины Т,характеризующее разброс результатов измерения вокруг измеряемой величины.
В силу предыдущего результат измерения есть также случайная величина (обозначим ее через X),связанная с Т зависимостью X = а+ Т . Отсюда: М(Х) = а,s (Х) =s (Т) = s и Xимеет нормальный закон распределения.
Заметим, что случайная ошибка измерения, как и результаты измерения, всегда выражаются в некоторых целых единицах, связанных с шагом шкалы измерительного прибора; в
144

теории удобнее считать случайную ошибку непрерывной случайной величиной, что упрощает расчеты.
При измерении возможны две ситуации:
а) известно s (это характеристика прибора и комплекса условий, при которых производятся наблюдения), требуется по результатам измерений оценить а;
б) s неизвестно, требуется по результатам измерений оценить а и s .
6.8. Неравенство Чебышева. Закон больших чисел
Лемма. Пусть X − случайная величина, принимающая только неотрицательные значения. Тогда
P(X ≥1) ≤ M (X ). |
(6.27) |
Теорема. Для любой случайной величины X при каждом положительном числе ε имеет место неравенство
P( |
|
X − M (X ) |
|
≥ ε) ≤ |
D(X ) |
. |
(6.28) |
|
|
||||||
|
|
|
|||||
|
|
|
|
|
ε 2 |
|
|
|
|
|
|
|
|
||
Неравенство (6.28) называют неравенством Чебышева.
Пример. Пусть случайная величина Xимеет D(X)=0.001. Какова вероятность того, чтоX отличается отМ(Х)более чем на 0.1?
Решение. По неравенству Чебышева
P( X − M (X ) ≥ 0.1) ≤ D0(.1X2) = 00.001.01 = 0.1.
Примечание. Отметим другую форму неравенства Чебышева. Так как событие, выражаемое неравенством
X − M (X ) < ε , противоположно событию, выражаемому неравенством X − M (X ) ≥ ε , то
P( X − M (X ) < ε)+ P( X − M (X ) ≥ ε) =1.
Отсюда получаем другую форму неравенства Чебышева:
145

P( |
|
X − M (X ) |
|
< ε) ≥1 − |
D(X ) |
. |
(6.29) |
|
|
||||||
|
|
|
|||||
|
|
|
|
|
ε 2 |
|
|
|
|
|
|
|
|
||
Теорема (теорема Чебышева; закон больших чисел). Ес-
ли дисперсии независимых случайных величин Х1,Х2, ...,Хп ограничены одной и той же постоянной С,D(Xi)≤ С (i = 1, 2,
..., n), то, каково бы ни было ε > 0, вероятность выполнения
|
|
|
|
|
|
|
|
1 |
|
|
неравенства |
|
− M ( |
X |
) |
< ε , где |
|
= |
(X1 + X2 + + Xn ), |
||
X |
||||||||||
X |
||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
будет сколь угодно близка к единице, если число случайных величин п достаточно велико, то есть
lim P( |
|
|
|
− M ( |
|
) |
|
< ε)=1. |
(6.30) |
|||||
|
X |
X |
|
|||||||||||
n→∞ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
Частный случай теоремы Чебышева. Если все Хkиме- |
||||||||||||||
ют одинаковые математические ожидания M(X1) |
= ... = |
|||||||||||||
M(Xn) = a и D(Xk) < C(k = l,2,...,n), то |
|
|||||||||||||
lim P( |
|
|
|
− a |
|
< ε)=1. |
(6.31) |
|||||||
|
|
|
|
|
||||||||||
X |
||||||||||||||
n→∞ |
|
|
|
|
|
|||||||||
|
|
|
||||||||||||
Сущность теоремы Чебышева состоит в следующем. Несмотря на то, что каждая из независимых случайных величинXk может принять значение, далекое от математического ожидания
М(Хk), среднее арифметическое Х достаточно большого числа случайных величин с большой вероятностью весьма близко к среднему арифметическомуих математических ожиданий.
Теорема Чебышева имеет большое практическое значение. Пусть, например, измеряется некоторая физическая величина. Обычно принимают в качестве искомого значения измеряемой величины среднее арифметическое результатов нескольких измерений. Можно ли считать такой подход верным? Теорема Чебышева (ее частный случай) отвечает на этот вопрос положительно.
На теореме Чебышева основан широко применяемый в статистике выборочный метод, согласно которому по сравни-
146
