
- •Закон сохранения заряда. Закон Кулона.
- •2. Уравнение непрерывности. Закон Ома для однородного участка проводника. Уравнение непрерывности
- •Закон Ома для однородного участка проводника
- •Сторонние силы. Эдс
- •Закон Ома для неоднородного участка цепи
- •Напряженность электростатического поля двух
- •Первое правило Кирхгофа
- •Переходные процессы в конденсаторах (зарядка конденсатора).
- •Формула 1 — закон электромагнитной индукции для движущегося точечного заряда
- •Формула 2 — модуль вектора индукции
- •Магнитное поле соленоида
- •Проводники в электрическом поле.
- •Зонная теория
- •Полупроводник n-типа
- •Полупроводник p-типа
- •16. Момент сил, действующий на контур с током
- •По модулю
- •После интегрирования получим
- •Плотность энергии электрического поля
- •Энергия заряженного конденсатора
- •. Индуктивность
- •1. Теорема Гаусса в интегральной форме
- •2. Теорема Гаусса в дифференциальной форме.
- •Электрическое поле равномерно заряженной плоскости
- •Энергия диполя
- •2.6.2. Теорема Гаусса для поля вектора электрического смещения
- •2.7. Связь между векторами и
Формула 1 — закон электромагнитной индукции для движущегося точечного заряда
Где r радиус-вектор, идущий от заряда к точке наблюдения
Q заряд
V вектор скорости движения заряда
![]()
Формула 2 — модуль вектора индукции
Где альфа это угол между вектором скорости и радиус вектором
Эти формулы определяют магнитную индукцию для положительного заряда. Если ее необходимо рассчитать для отрицательного заряда то нужно подставить заряд со знаком минус. Скорость движения заряда определяется относительно точки наблюдения.
Билет №7
1. Циркуляция вектора напряженности электрического поля. Связь между напряжённостью электростатического поля и потенциалом
Электростатическое поле является консервативным (потенциальным), следовательно, работа кулоновских сил на замкнутой траектории должна равняться нулю. Действительно, из формулы (16) следует, что работа на замкнутой траектории равна нулю, так как r1 = r2.
Если
в качестве пробного заряда, переносимого
из 1 в 2 данного электростатического
поля
,
взять единичный, положительный заряд
(например, в СИ, qo=
+1 Кл), то элементарная работа консервативных
кулоновских сил поля при перемещении
его на малый отрезок

 (21)
(21)
Полная работа на всем пути 12
 .
(22)
.
(22)
Циркуляцией
вектора
по произвольному замкнутому пути L
называют интеграл
 .
Так как на замкнутой траектории работа
консервативных кулоновских сил равна
нулю, то циркуляция вектора
электростатического поля равна нулю,
т. е.
.
Так как на замкнутой траектории работа
консервативных кулоновских сил равна
нулю, то циркуляция вектора
электростатического поля равна нулю,
т. е.
 (23)
(23)
Это положение называют теоремой о циркуляции вектора .
Замечание:
справедливо и обратное утверждение:
если циркуляция вектора
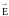 электростатического поля равна нулю,
то такое поле является потенциальным.
электростатического поля равна нулю,
то такое поле является потенциальным.
Связь между Е и
Согласно для единичного, положительного заряда (qo= +1 Кл) имеем
 .
(31)
.
(31)
Формула
(31) остается справедливой не только для
конечных, но и для элементарных перемещений
 ,
т. е.
,
т. е.
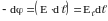
или
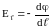 .
(32)
.
(32)
Следовательно,
проекция вектора
 на направление
равна со знаком минус первой производной
потенциала по данному направлению.
на направление
равна со знаком минус первой производной
потенциала по данному направлению.
Если
перемещение
параллельно оси Х, то
= dx,
где
единичный вектор оси Х; dx
приращение
координаты х. Исходя из этого, получим
dx,
где
единичный вектор оси Х; dx
приращение
координаты х. Исходя из этого, получим
(
)
= dx
= Exdx,
dx
= Exdx,
где Ех проекция вектора на ось Х.
Значит, с учетом (1.55) последнее выражение запишем в виде
 ,
(33)
,
(33)
где
символ частной производной
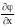 свидетельствует о том, что функцию
свидетельствует о том, что функцию
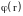 =
(х, у, z)
необходимо дифференцировать только по
х, считая у, и z постоянными.
=
(х, у, z)
необходимо дифференцировать только по
х, считая у, и z постоянными.
Аналогично можно найти выражения для проекций Еу и Еz, т. е.
 ,
,
 ,
,
 .
.
Зная проекции вектора на оси координат можно найти и сам вектор,
 .
(34)
.
(34)
В
формуле (34) выражение в скобках является
градиентом потенциала
(grad
или
 ).
Таким образом,
).
Таким образом,
= grad = . (35)
Знак «» означает, что вектор направлен в сторону убывания потенциала; векторный оператор «набла».
2. Магнитный поток. Циркуляция вектора индукции магнитного поля. Теорема о циркуляции вектора (В).
Густота
силовых линий прямо пропорциональна
модулю вектора индукции. Если в
неоднородное магнитное поле поместить
площадку dS,
в пределах которой магнитное поле
считается однородным, то силовые линии
пронизывают ее. В этом случае площадку
dS
пронизывает магнитный поток (рис. 5):
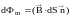 (19)
(19)
Рис.
5
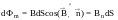 .
(20)
.
(20)
Тогда суммарный магнитный поток:
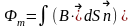 .
(21)
.
(21)
Если магнитное поле однородно, то магнитный поток
Фm= ВScosa. (22)
При a = 0о магнитный поток максимален, Фm= ВS. Магнитный поток измеряется в веберах (Вб).
(Теорема
Гаусса для вектора
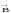 )
Магнитный поток пронизывающий произвольную
замкнутую поверхность, равен нулю
)
Магнитный поток пронизывающий произвольную
замкнутую поверхность, равен нулю
Число силовых линий, выходящих равно ввходящим в область, ограниченную этой поверхностью, и не зависит от формы и размеров ее.
Циркуляция вектора индукции магнитного поля
Это
криволинейный интеграл по произвольному
контуру L
скалярного произведения вектора индукции
 и вектора элемента этого контура
и вектора элемента этого контура

 ,
(6.25)
,
(6.25)
где
 -
проекция
-
проекция
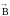 на
на
 .
.
Теорема о циркуляции вектора (В).
Циркуляция
 по произвольному контуру L
в вакууме равна произведению магнитной
постоянной 0
на алгебраическую сумму токов, охваченных
этим контуром.
по произвольному контуру L
в вакууме равна произведению магнитной
постоянной 0
на алгебраическую сумму токов, охваченных
этим контуром.
Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта, а ток противоположного направления отрицательным (рис. 6.7, где I1 > 0, I3 > 0, I2 < 0, I4 < 0).
Рис.6.7.
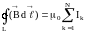
 .
.
Билет №8
1. Эквипотенциальные поверхности, их связь с силовыми линиями
Рис.
9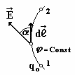
Поверхность, геометрическое место точек которой имеют одинаковый потенциал, называют эквипотенциальной.
При
перемещении по эквипотенциальной
поверхности на произвольный отрезок
 потенциал остается неизменным (d
= 0).
потенциал остается неизменным (d
= 0).
Тогда
касательная составляющая вектора
к поверхности равна нулю ( =
0). Следовательно, вектор
в каждой точке направлен по нормали к
эквипотенциальной поверхности.
Действительно, будем перемещать пробный
заряд q0 вдоль
эквипотенциальной поверхности из точки
1 в точку 2 (рис. 9). Допустим, что вектор
направлен произвольно к поверхности
под углом . При
перемещении пробного заряда в электрическом
поле должна совершаться работа. Используя
формулы, (15а) и (29) получаем
=
0). Следовательно, вектор
в каждой точке направлен по нормали к
эквипотенциальной поверхности.
Действительно, будем перемещать пробный
заряд q0 вдоль
эквипотенциальной поверхности из точки
1 в точку 2 (рис. 9). Допустим, что вектор
направлен произвольно к поверхности
под углом . При
перемещении пробного заряда в электрическом
поле должна совершаться работа. Используя
формулы, (15а) и (29) получаем
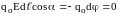 ,
так как = const.
,
так как = const.
Из последнего выражения следует, что cos = 0 при = 90о. Следовательно, вектор перпендикулярен касательной к эквипотенциальной поверхности в данной точке. Таким образом, линии напряженности проводятся всегда
Рис.
10
2. Дифференциальная форма теоремы о циркуляции вектора (В). Магнитное поле соленоида.
Рассмотрим
отношение циркуляции вектора
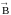 к площадке S,
натянутой на контур L.
Ориентация этого контура связана с
вектором нормали
к площадке S,
натянутой на контур L.
Ориентация этого контура связана с
вектором нормали к плоскости контура правилом правого
винта. В пределе при S
0, имеем
к плоскости контура правилом правого
винта. В пределе при S
0, имеем
 .
(6.29)
.
(6.29)
Формулу (6.29) называют ротором поля .
Следовательно,
этот предел представляет собой скалярную
величину, равную проекции вектора
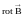 на нормаль. Используя (6.29), формулу (6.28)
представим в виде
на нормаль. Используя (6.29), формулу (6.28)
представим в виде
 (6.30)
(6.30)
или
 ,
(6.31)
,
(6.31)
где

векторный дифференциальный оператор.
векторный дифференциальный оператор.
Следовательно,
 .
(6.32)
.
(6.32)
Ротор
поля
 совпадает по направлению с вектором
плотности тока
совпадает по направлению с вектором
плотности тока
 в данной точке. Формула (6.32)
дифференциальная форма теоремы о
циркуляции
в данной точке. Формула (6.32)
дифференциальная форма теоремы о
циркуляции
 .
Дифференциальная форма теоремы о
циркуляции
.
Дифференциальная форма теоремы о
циркуляции
 расширяет ее возможности для исследования
и расчета сложных магнитных полей.
расширяет ее возможности для исследования
и расчета сложных магнитных полей.
