2.6. Функционалы, содержащие производные высшего порядка
Рассмотрим функционал вида
с граничными условиями
Применяя необходимое условие экстремума (7) и рассуждая, как при выводе уравнения (16), получим уравнение Эйлера
.
(17)
При этом слагаемое
надо интегрировать по частям один раз,
а слагаемое
- два раза. Получим обыкновенное
дифференциальное уравнение четвёртого
порядка. Четырех граничных условий как
раз достаточно, чтобы получить частное
решение (17),реализующее экстремум.
Функционалы с производными порядка до k>2 включительно рассматриваются аналогично. Уравнение Эйлера для такого функционала имеет порядок 2k. Иногда это уравнение называют уравнением Эйлера-Пуассона.
Пример8. Найти экстремаль функционала
при граничных условиях
.
Решение. Так как в данном случае
,
то уравнение Эйлера (17) имеет вид
или
.
Его общим решением будет многочлен
.
Используя граничные условия, получим
.
Таким образом, экстремум может достигаться
лишь на прямой y=x.
Пример9. Найти экстремаль функционала
при граничных условиях
.
Решение. Здесь
.
Поэтому уравнение Эйлера (1) в данном
случае имеет вид
или
.
Решением его, используя характеристичекое
уравнение.
.
Общее решение для этих корней имеет вид
.
Воспользуемся граничными условиями
.
Сложим
все уравнения. Получаем
.
Теперь второе уравнение умножим на
и сложим с третьим. Имеем
или
.
Отсюда следует, что
,
т.е.
.
Значит,
и
а
.
Таким образом, экстремум может достигаться
лишь на кривой
.
2.7. Функционалы от нескольких функций
Функционал может зависеть не от одной, а от нескольких функций одной переменной. Это встречается, например в задачах на экстремум, где искомой является не плоская, а пространственная линия. Пусть функционал
зависит от двух функций
и
,
заданных при
.
Эти функции между собой не связаны –
одну из них можно фиксировать, а другую
произвольно варьировать. Фиксируя
и
варьируя
мы получаем частную
,
аналогичную частному дифференциалу:
.(18)
Аналогично получается частная вариация
по
(19)
Если заданы простейшие граничные условия
то для функций
и
,
реализующих экстремум, обе частные
вариации должны равняться нулю , т.к.
при этом функционал превращается в
функционал, зависящий лишь от одной
варьируемой функции
или
,
то по аналогии с п.2.5.2 получим систему
уравнений Эйлера
,
(
)
Общее решение этой системы двух обыкновенных дифференциальных уравнений второго порядка содержит четыре произвольные постоянные, которые определяются из четырёх условий.
Аналогично рассматривается функционалы, зависящие от большего числа функций, а также функционалы, зависящие от нескольких функций и выражающееся через производные более высоких порядков.
Пример 10. Найти экстремали функционала.
Решение.
Здесь
и приходим к уравнению
.
Решаем его с помощью характеристического
уравнения (см. пример 9):
.
Используя граничные условия, получаем систему.
Сложим первое и третье и второе и
четвёртое уравнение. Получаем:
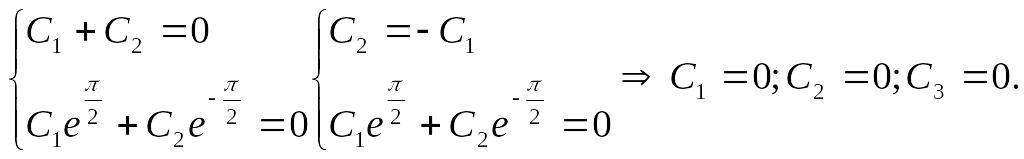
Из второго уравнения выведем четвёртое:
Следовательно, y=sinx; z=-sinx.
Задачи для самостоятельного решения
1. Найти экстремали функционала
.
2. Исследовать на экстремум функционал
.
3. Исследовать на экстремум функционал
.
4. Найти экстремали функционала
.
5. Найти экстремали функционала
.
6. Найти экстремали функционала
.
7. Найти экстремали функционала
.
8. Найти экстремали функционала
.
9. Найти экстремали функционала
.
10. Найти экстремали функционала
.
11. Найти экстремали функционала
12.
.
13. Найти экстремали функционала
.
14. Найти экстремали функционала
.
15. Найти экстремали функционала
.
16. Найти экстремали функционала
.
17. Найти экстремали функционала
.
18. Найти экстремали функционала
.
19. Найти экстремали функционала
.