6. Вариационные принципы

Каждый вариационный принцип утверждает, что для некоторого класса задач, если заданы условия задачи, то из всех мыслимых состояний, процессов и т.п., в определённом смысле совместимых с этими условиями, на самом деле реализуется такое состояние, такой процесс, которые придают некоторому характерному для этого принципа функционалу стационарное значение.

Иногда говорят не о стационарном, а об экстремальном значении. Таким образом, вариационный принцип характеризуется указанием класса задач, понятием совместимости сравниваемых процессов с условиями задачи и определённого на этих процессах функционала, который должен принимать стационарное значение.

Имеются две основные группы вариационных принципов. Один- «традиционный» -связан с задачами физики, математики. Другая группа вариационных принципов развилась сравнительно недавно и имеет дело с задачами регулирования, математической экономики и т. п. здесь речь идёт о выработке в заданных условиях определённой стратегии, обеспечивающей максимальную пользу.

6.1 . Принцип Гамильтона в простейшем случае

Этот принцип является одним из наиболее универсальных принципов современного естествознания. Рассмотрим его сначала на простом примере.

Пусть материальная точка массы может двигаться по оси OX. Тогда закон движения должен удовлетворять второму закону Ньютона

. (55)

Обозначим первообразную по для функции через , положив .

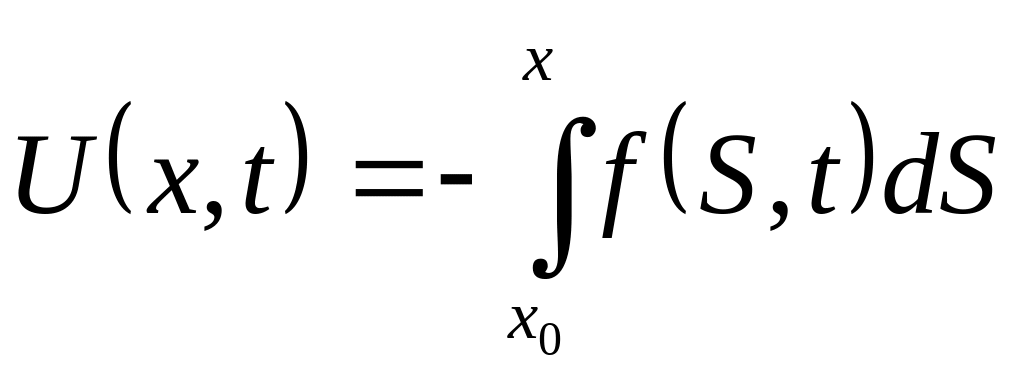Это потенциал рассматриваемого силового поля. Кроме того, обозначим .

Это кинетическая энергия движущейся точки. В таких обозначениях уравнение (53) можно переписать в виде

(56)

Заметим, что не зависит от скорости , а - от и обозначим

- функция Лагранжа рассматриваемой механической системы. Теперь уравнение (56) можно представить в виде

(57)

Но это уравнение является уравнением Эйлера для функционала

(58)

Этот функционал носит название действие.

В силу предыдущего условие его стационарности при фиксированных значениях , полностью равносильно уравнению (55). Следовательно, дифференциальный закон Ньютона можно сформулировать следующим образом: если заданные начальное и конечное состояние системы, то из всех возможных законов движения на самом деле реализуется такой, для которого действие принимает стационарное значение.

В этом состоит вариационный принцип Гамильтона. Из вида функционала (58) следует, что для любого реального закона движения точки на любом достаточно малом интервале времени действие принимает не просто стационарное, а минимальное значение. Поэтому принцип Гамильтона часто называют также принципом минимального действия, хотя для больших промежутков времени действие будет иметь не минимальное, а максимальное значение.

6.2. Принцип Гамильтона для систем с конечным числом степеней свободы

Рассмотрим теперь систему дифференциальных уравнений, обозначающих уравнение (55):

.

Этим уравнениями описывается, например, система из точек в пространстве, на которые не наложено никаких связей и действуют силы, зависящие от координат всех точек, и от времени. При этом - декартовы координаты первой точки массы ; - координаты второй точки массы и т. д. - число степеней свободы такой системы.

Пусть силовое поле потенциал , т. е. сила, действующая на -ю точку, имеет проекции на оси, равные

(59)

Такой потенциал (потенциальная энергия системы), в отличие от п. 6.1, имеется не всегда, а только для потенциальных полей. Признаком потенциальности поля служат равенства

Известно, что равно работе, которую совершает силовое поле в фиксированный момент времени при переводе системы из любого текущего состояния в некоторое заданное . При этом такая работа не должна зависеть от способа перевода, что и является критерием потенциальности.

Произвольность выбора конечного состояния равносильна добавлению к произвольной функции времени, что не влияет на результат.

Обозначим ;

Рассуждая так же , как и в п. 6.1, приходим к тому же выводу о стационарности действия, т. е. интеграла

для реального закона движения.

В этой же формулировке принцип Гамильтона справедлив для случая, когда движение системы подчинено голономным связям

(60)

Тогда в формулировке принципа Гамильтона сравнению подлежат только законы движения совместимые с этими связями. Таким образом, приходим к задаче об условно стационарном значении.

Эта условность не всегда удобна. Чтобы избавиться от неё, обычно выбирают обобщённые координаты. (где - число степеней свободы в системе), характеризующих положение системы. Через них выражаются координаты точек системы

(61)

Это является общим решением системы (60) в параметричес-кой форме. Так же выражаются и потенциал , кинетическая энергия , функция Лагранжа .

Так как уравнения связей учтены теперь выбором координат , то мы приходим к задаче на безусловное стационарное значение функционала

(62)

при заданных начальном и конечном состояниях системы.

Покажем, что исходя из принципа Гамильтона, можно получить уравнения динамики. Действительно, если (действие принимает стационарное значение), то уравнения Эйлера для данного функционала имеют вид

,

В простейшем случае получаем

,

Таким образом, приходим к уравнениям динамики

, ,