В.Н. Дурова М.И. Зайцева В.Н. Макаров

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ

Учебное пособие

Воронеж 2006

Воронежский государственный технический университет

В.Н. Дурова М.И. Зайцева В.Н. Макаров

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ

Утверждено Редакционно-издательским советом

университета в качестве учебного пособия

Воронеж 2006

Введение

Пособие написано в соответствии с образовательным стандартом специальностей 160201 «Самолето-и вертолетостроение,130501 «Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ», 220501 «Управление качеством».. Длинное пособие предназначено для проведения лекционных занятий по теме «Элементы вариационного исчисления» Большинство рассматриваемых вопросов предназначено для самостоятельного изучения студентами. С целью облегчения самостоятельной работы студентов изложение материала сопровождается большим количеством подробно решенных задач вариационного исчисления Приводятся примеры для самостоятельного решения.

Перед изучением излагаемых вопросов следует повторить темы математического анализа «Полный дифференциал»

1. Основные понятия

1. Функционал

Наряду с задачами, в которых необходимо определить минимальные и максимальные значения некоторой функции y=f(x), в задачах физики нередко возникает необходимость найти максимальные или минимальные значения величины особого рода, называемых функционалами. Понятие функционала является обобщением понятия функции.

Определение.

Пусть М-множество некоторых функций.

Если каждой функции ставится в соответствие определенное число, то говорят, что на множестве М задан функционал.

и Таким образом, если функция устанавливает соответствие между двумя числовыми множествами Х (область определения) и Y (область значений), то функционал устанавливает соответствие между множеством функций множеством чисел. Можно сказать, что функционалы – это переменные величины, значения которых определяются выбором одной или нескольких функций. Аналогично определяются и функционалы, зависящие от нескольких функций, а также функционалы от функций нескольких независимых переменных.

П ример 1. Пусть М-множество функций y(x), область определения которых содержит точку . Значение функций y(x) в точке образует функционал .

П

y

ример 2. Пусть М-множество функций y(x), имеющих непрерывную производную на отрезке . Тогда длина дуги плоской кривой, соединяющей две заданные точки и , есть функционал

.

Пример 3. Площадь S некоторой поверхности также является функционалом, так как она определяется выбором поверхности, т.е. выбором функции , входящей в уравнение поверхности :

,

где D-проекция поверхности на плоскость XOY.

Другие примеры (из механики): моменты инерции, статические моменты, координаты центра масс некоторой однородной кривой или поверхности также являются функционалами, т.к. их значения определяются выбором кривой или поверхности.

1.2. Предмет вариационного исчисления

Вариационное исчисление изучает методы, позволяющие находить максимальные и минимальные значения (экстремумы) функционалов. Задачи, в которых требуется исследовать функционал на экстремум, называются вариационными задачами.

Многие законы физики и механики состоят в утверждении, что некоторый функционал в рассматриваемом процессе должен достигать максимума или минимума. В такой формулировке эти законы называются вариационными принципами механики или физики. К числу таких вариационных принципов или простейших следствий из них принадлежат: принцип наименьшего действия, закон сохранения энергии, закон сохранения импульса, закон сохранения количества движения и т.д.

Б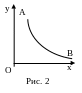 ольшое влияние на развитие вариационного исчисления оказали следующие три задачи.

Задача о брахистохроне (1696г, Иоганн Бернулли).

В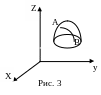 этой задаче требуется определить линию, соединяющую две заданные точки А и В, не лежащие на одной вертикальной прямой, и обладающую тем свойством, что материальная точка, скатится по этой линии из точки А в точку В в кратчайшее время (рис. 2). Трение при этом не учитывается. Легко видеть, что линией быстрейшего ската не будет прямая, соединяющая точки А и В, хотя она и является кратчайшим расстоянием между этими точками. При движении по прямой скорость будет возрастать сравнительно медленно. Если же взять кривую, более круто спускающуюся вниз около точки А, то хотя путь и удлинится, но значительная часть пути будет пройдена с большей скоростью. Решение этой задачи было дано И. Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопиталем.

З

X

Z

адачи о геодезических линиях. Требуется определить линию наименьшей длины, соединяющую две данные точки на

некоторой поверхности (рис. 3). Такие кратчайшие линии называются геодезическими.

Получается типичная вариационная задача на так называемый связанный или условный экстремум. Необходимо найти минимум функционал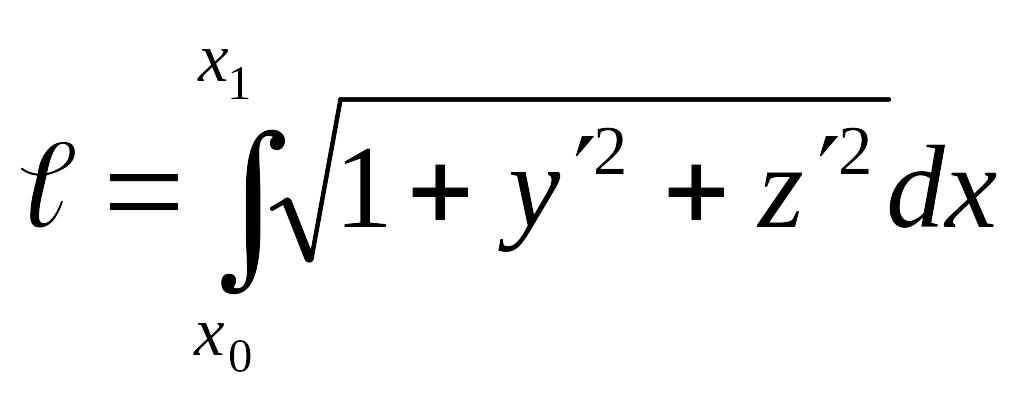а , при чем функции y(x) и z(x) должны удовлетворять условию . Эта задача была решена в 1698 году Я. Бернулли. Однако общий метод решения задач такого типа был дан лишь в работах Л. Эйлера и Ж. Лагранжа.

Изопериметрическая задача. Требуется найти замкнутую линию данной длины , ограничивающую максимальную площадь S. Такой линией, как было известно еще в древней Греции, является окружность. В этой задаче требуется определить экстремум функционала S при дополнительном условии – длина кривой должна быть постоянна, т.е. функционал

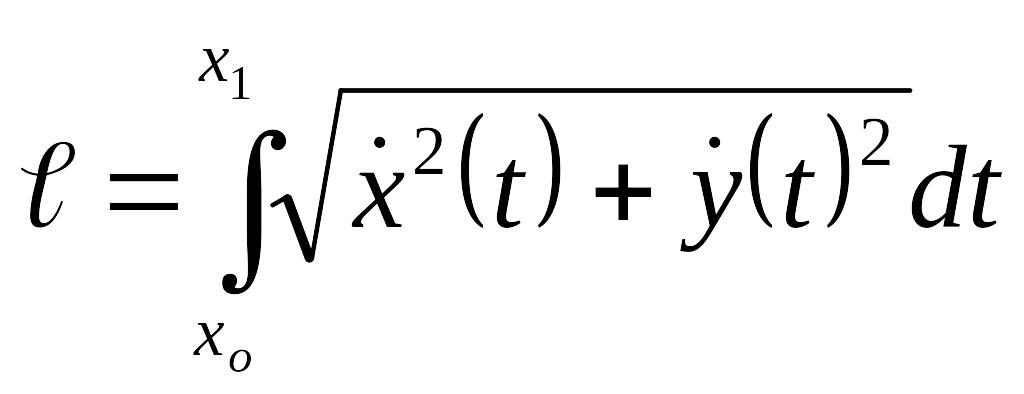
сохраняет постоянное значение. Условия такого типа называются изопериметрическими. Общие методы решения таких задач были разработаны Л. Эйлером.

Вариационное исчисление оформилось в самостоятельную математическую дисциплину с собственными методами исследования после фундаментальных работ Эйлера. Своим названием «вариационное» исчисление обязано методу вариации, при помощи которого решаются экстремальные задачи.