2.4.3. Формула парабол (Симпсона)

Формула парабол, предложенная английским математиком Симпсоном, основана на замене функции f(x) на отрезках длиной дугой параболы (рис. 2.10).

Рис. 2.10

Разобьем отрезок на четное число 2n равных отрезков

.

Через каждые 3 точки проводится дуга параболы . Таким образом, на участке кривая f(x) заменяется параболой. Мы осуществили кусочно квадратичную аппроксимацию. Площадь, ограниченную одной из парабол, нетрудно подсчитать:

.

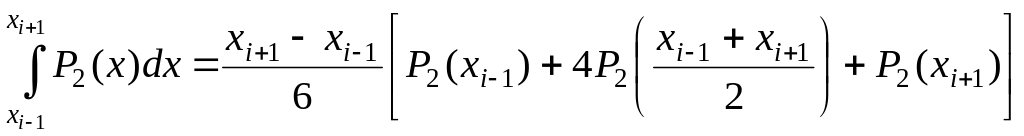Суммируя эти площади, в результате найдем приближенное значение интеграла

.

Заданная точность вычисления достигается за значительно меньшее число операций.

3. Несобственные интегралы

Понятие интеграла было введено для функций, непрерывных на конечном отрезке. Однако при рассмотрении математических моделей многих явлений (процессов) целесообразно обобщение понятия интеграла. Во-первых, иногда полезно рассмотрение бесконечных пределов интегрирования. Во-вторых, интегрируемая функция может иметь разрывы. В связи с изложенным мы рассмотрим эти ситуации и дадим соответствующие обобщения понятию интеграла.

3.1. Несобственные интегралы с бесконечными пределами интегрирования

Пусть т. е. функция f(x) непрерывна на отрезке при любом b > a.

Интеграл

(3.1)

называется несобственным интегралом.

Говорят, что несобственный интеграл сходится, если существует конечный предел (3.1). Если не существует конечного предела (3.1), то несобственный интеграл называют расходящимся.

С геометрической точки зрения величина (3.1) выражает площадь бесконечной фигуры, ограниченной кривой осью абсцисс и прямой x = a (рис. 3.1).

Аналогично вводятся и другие несобственные интегралы с бесконечными пределами интегрирования

где выбирается произвольно (докажите самостоятельно, что от выбора c значение интеграла не зависит). Для последнего интеграла сходимость определяется сходимостью обоих интегралов в правой части равенства.

Рассмотренные несобственные интегралы называют иногда несобственными интегралами первого рода.

3.2. Несобственные интегралы от разрывных функций

Пусть , а в точке x = b она имеет разрыв второго рода. Тогда интеграл

(3.2)

н азывается несобственным интегралом (сходящимся, если предел (3.2) существует и конечен; расходящимся – в остальных случаях). Несобственные интегралы от разрывных функций называют ещё несобственными интегралами второго рода.

Геометрический смысл несобственного интеграла ясен из рис. 3.3.

Аналогично вводятся несобственные интегралы в случаях, когда подынтегральная функция имеет иначе расположенную точку разрыва. Так, если f(x) имеет разрыв при x = a, т. е. , то

(3.3)

Если точка разрыва x = с лежит между точками x = a и x = b, то

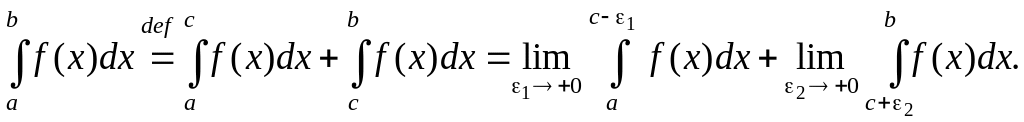(3.4)

3.3. Теоремы о сходимости несобственных интегралов

Вопрос о сходимости несобственного интеграла в ряде случаев можно решить без его вычисления. Это особенно важно, когда первообразную через элементарные функции в конечном виде выразить невозможно. Рассмотрим простейшие теоремы относительно сходимости несобственных интегралов с бесконечными пределами.

Теорема 1. Если и интеграл сходится, то сходится и интеграл Если при тех же предположениях интеграл расходится, то расходится и интеграл .

Доказательство

Е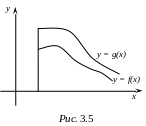 сли существует, то представляет величину ограниченную и монотонно возрастающую. Так как , значит, и площадь, ограниченная этой кривой, меньше, чем площадь под кривой g(x) (рис. 3.5). Значит, существует и .

Вторая часть теоремы доказывается аналогично.

Теорема 2. Если сходится интеграл то сходится и интеграл .

Н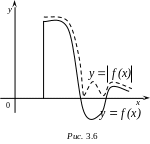 е приводя доказательства этой теоремы, заметим, что в первом интеграле суммируются площади, лежащие над и под осью абсцисс, а во втором интеграле площади под осью абсцисс учитываются со знаком минус (рис. 3.6). Поэтому первый интеграл сходится «труднее»: он может расходиться в тех случаях, когда второй интеграл сходится.

Если интеграл сходится, то интеграл называется абсолютно сходящимся.

Если интеграл сходится, а расходится, то первый интеграл называется условно сходящимся.

Теорема 3. Если и существует конечный ненулевой предел то интегралы , либо оба сходятся, либо оба расходятся.

Доказательство этой теоремы не приводим.

Наиболее часто при выяснении вопроса о сходимости несобственного интеграла выполняют сравнение его с интегралом от степенной функции

(3.6)

который сходится при p > 1 и расходится при p

Действительно,