1.9. Интегрирование тригонометрических функций
1. Интегралы вида , где r – рациональная функция
Интегралы
указанного вида приводятся к интегралам
от рациональных функций с помощью так
называемой универсальной
тригонометрической подстановки
.
В результате этой подстановки имеем
;
;
.
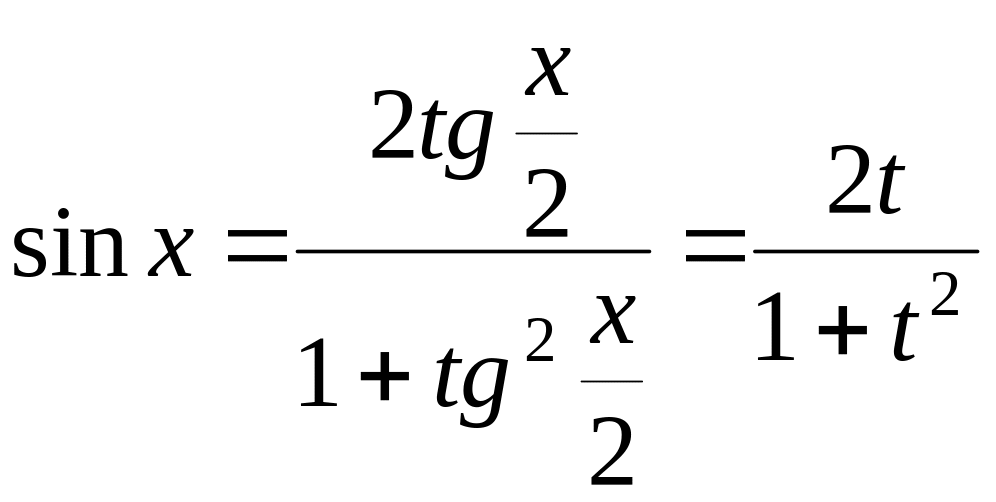2. Интегралы вида
Выделим два случая решения такого интеграла:
1)
если n
– нечетное положительное число, то
применяется подстановка
;
если же m
– нечетное положительное число, то
подстановка
;
2) если оба показателя степени m и n – четные положительные числа, то следует преобразовать подынтегральную функцию с помощью формул
,
,
.
3. Интегралы
вида
и
,
где m
– целое положительное число
При нахождении таких интегралов применяются формулы
или
,
с помощью которых последовательно понижается степень тангенса или котангенса.
4. Интегралы
вида
,
,
Тригонометрические формулы
,
,
дают возможность представить произведение тригонометрических функций в виде суммы.
5. Тригонометрические подстановки
Интегралы вида
,
,
приводятся от рациональной относительно
и
функции с помощью тригонометрических
подстановок:
-
или
;
-
или
;
-
или
.
6. Интегралы вида
Интеграл
данного вида может быть преобразован
к интегралу вида
,
который был рассмотрен в п. 1.9.5.
Произведем преобразования трехчлена, стоящего под корнем:
.
Сделаем
замену переменной, положив
.
Тогда
.
Рассмотрим все возможные случаи.
Пусть ,
.
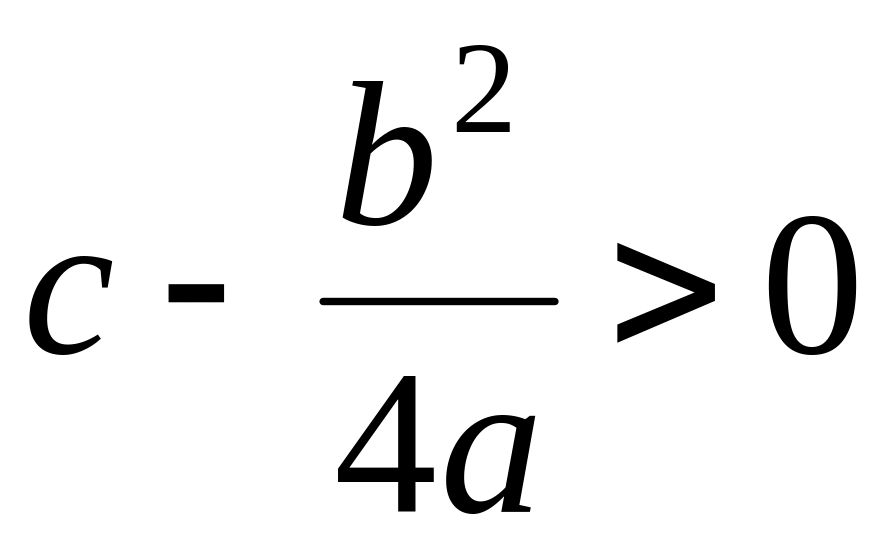Введем обозначения
,
.
В этом случае будем иметь
.
Пусть ,
.
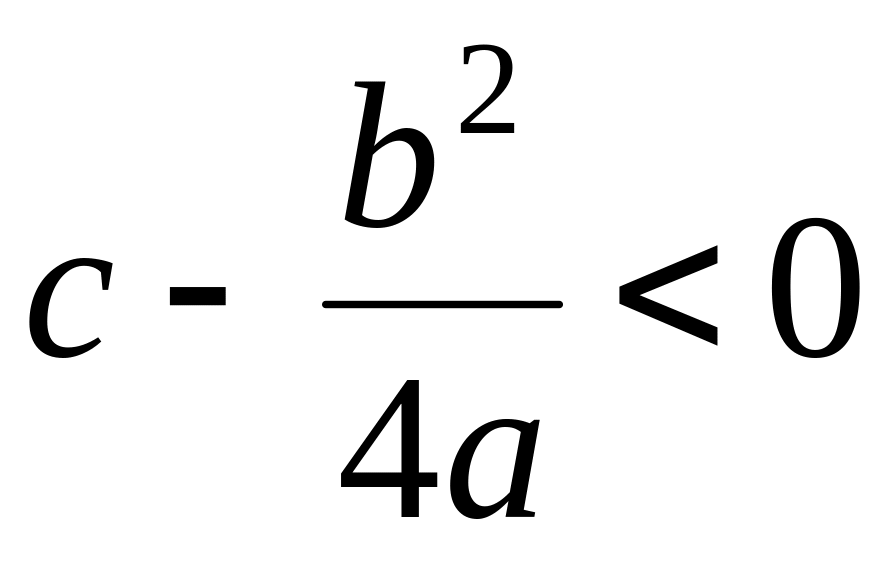Тогда
,
.
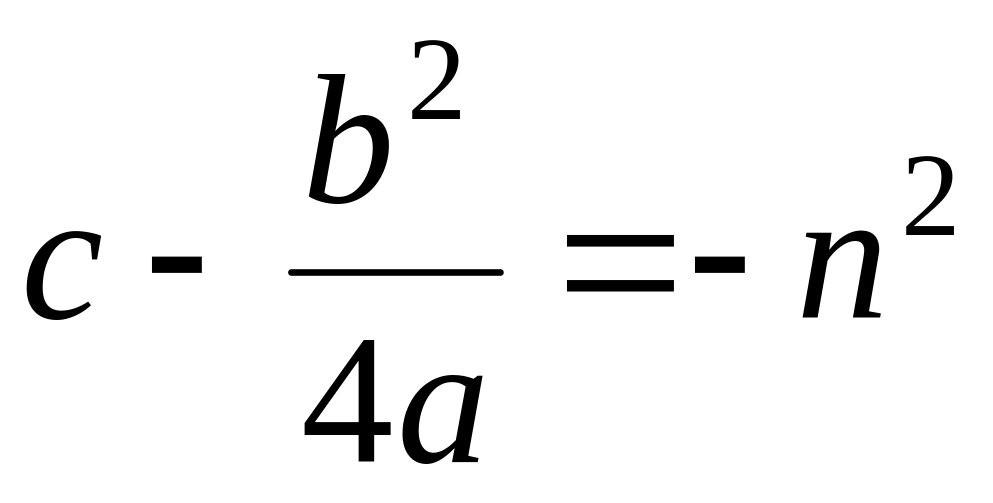Следовательно,
.
Пусть
,
.
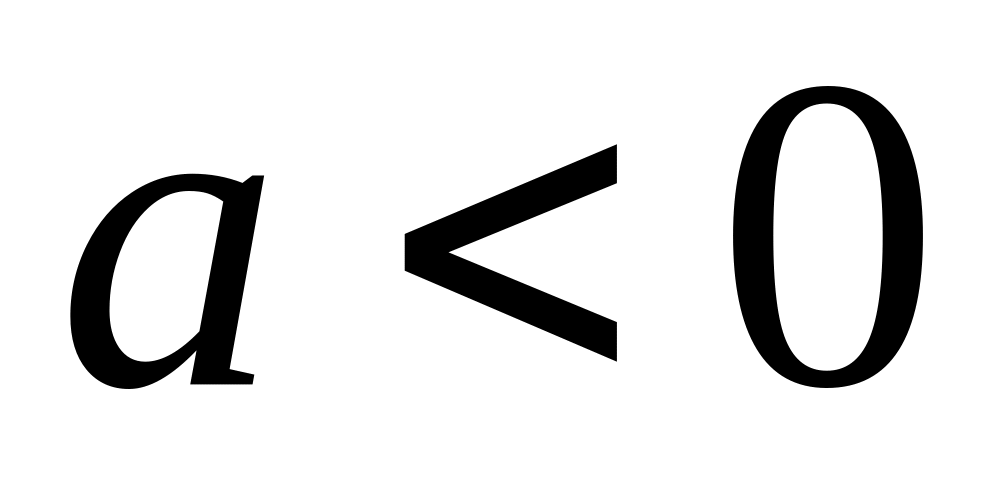Тогда
,
.
Следовательно,
.
Пусть , . В этом случае
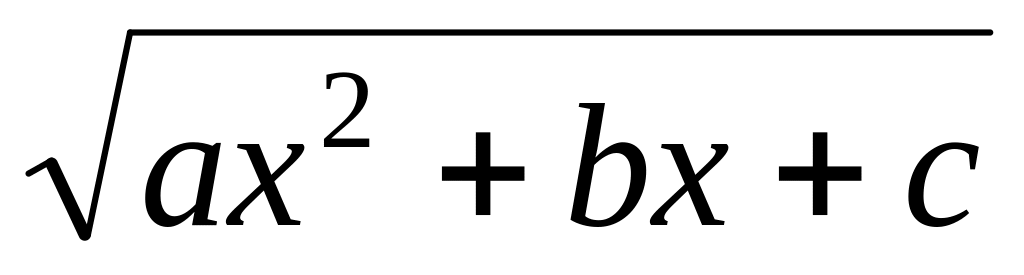есть комплексное число при любом x.
Таким образом, данный интеграл преобразуется к одному из следующих типов интегралов:
,
,
,
которые сводятся к интегралам, рассмотренным в п. 1.9.5.
1.10. Функции, интегралы от которых не выражаются через элементарные функции
В
п. 1.1 отмечалось, что всякая функция
f(x),
непрерывная на интервале (a,
b),
имеет на этом интервале первообразную,
т. е. существует такая функция F(x),
что
Однако не всякая первообразная, даже
тогда, когда она существует, выражается
в конечном виде через элементарные
функции. Таковы первообразные, выраженные
интегралами
,
,
,
,
,
и многие другие.
Во
всех подобных случаях первообразная
представляет собой некоторую новую
функцию, которая не сводится к комбинации
конечного числа элементарных функций.
Так, например, та из первообразных
,
которая обращается в нуль при x
= 0, называется
функцией
Лапласа и
обозначается Ф(х).
Таким образом,
,
если Ф(0) = 0.
Эта функция хорошо изучена. Составлены подробные таблицы ее значений при различных значениях х.
Та
из первообразных
,
которая обращается в нуль при x
= 0, называется
эллиптическим
интегралом
и обозначается Е(х),
т. е.
,
если Е(0) = 0.
Для этой функции также составлены таблицы значений при различных значениях х.