1.4. Замена переменной в неопределенном интеграле. Интегрирование подстановкой
Выполним
в интеграле
формальную замену переменной интегрирования
(1.6)
Проверим полученную формулу, вычислив производные по x от левой и правой частей равенства:
Таким образом, формула (1.6) доказана. При этом считалось, что
Формула
(1.6) выражает метод
интегрирования подстановкой, или
метод замены
переменной интегрирования. Этот
метод целесообразно использовать в тех
случаях, когда интеграл в правой части
равенства (1.6) проще, чем в левой. После
вычисления нового интеграла приходится
возвращаться к старой переменной, для
чего находят обратную функцию
1.5. Интегрирование по частям
Второй из основных методов интегрирования базируется на формуле, выражающей дифференциал произведения:
Отсюда имеем
или, рассматривая левую и правую части равенства как подынтегральные выражения, получаем
(1.7)
Произвольная постоянная в правой части равенства не пишется.
Формула
(1.7) выражает метод
интегрирования по частям. Этот
метод уместно использовать в тех
случаях, когда функция u(x)
при
дифференцировании упрощается. Поэтому
в качестве u(x)
выбирают
функции
(по возрастанию сложности).
1.6. Интегрирование функций, содержащих квадратный трехчлен
1.
Интегралы вида
.
Выделим полный квадрат в знаменателе дроби:
.
В
зависимости от знака выражения
интеграл сведется
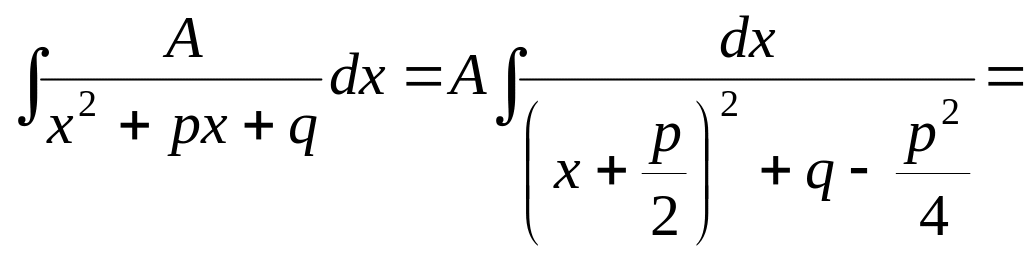
2.
Интегралы вида
.
Выделим в числителе производную от знаменателя. Для этого числитель представим в виде
.
Тогда
.
В первом интеграле числитель является производной от знаменателя. Поэтому
.
Второй интеграл рассмотрен в п. 1.
3.
Интегралы вида
.
Выделим полный квадрат в подкоренном выражении
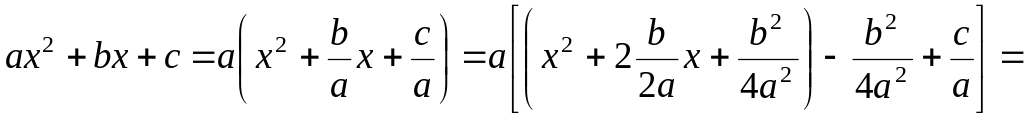
Интеграл сведется к табличным интегралам 15 или 16.
4.
Интегралы вида
.
Для нахождения этого интеграла выделим в числителе производную квадратного трехчлена, стоящего под знаком корня, и разложим интеграл на сумму двух интегралов
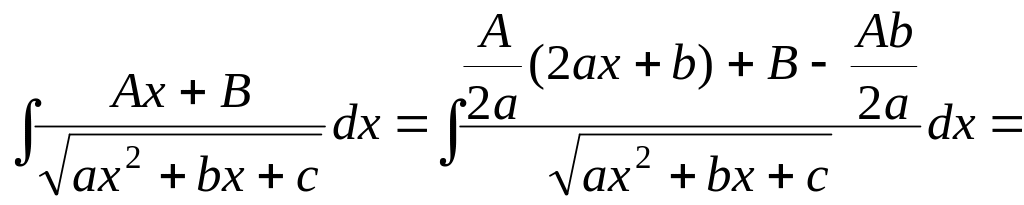
Первый из интегралов есть табличный интеграл
,
а второй рассмотрен в п. 3.
1.7. Интегрирование рациональных дробей
1.7.1. Интегрирование простейших дробей
Рациональной
дробью
называется дробь вида
,
где P(x)
и Q(x)
– многочлены. Рациональная дробь
называется правильной,
если степень многочлена P(x)
ниже степени многочлена Q(x);
в противном случае дробь называется
неправильной.
Простейшими (элементарными) дробями называются правильные дроби следующего вида:
А.
.
Б.
,
где m
– целое число, большее единицы.
В.
.
Г.
,
где n
– целое число, большее единицы.
Рассмотрим интегралы от простейших дробей:
А.
.
Б.
.
Вычисление интегралов от функций типа В было рассмотрено ранее в п. 1.6 «Интегрирование функций, содержащих квадратный трехчлен».
Г.
Рассмотрим теперь частный случай
интеграла от простейшей дроби типа Г.
Для интеграла
(n
– целое положительное число) имеет
место следующая рекуррентная формула:
.
Эта
формула позволяет после (n-1)-кратного
применения свести данный интеграл In
к табличному интегралу
.