8.2.2. Определение криволинейного интеграла по координатам

Г ладкую кривую подобно прямой линии можно ориентировать, задав на ней направление. Такие кривые называются ориентированными (рис. 8.6).

Пусть задано векторное поле

и некоторая ориентированная кривая l, гладкая между точками А и В. Элемент дуги этой кривой

.

Он является ориентированным элементом дуги. Следовательно, dx, dy, dz могут рассматриваться как проекции на соответствующие оси. Тогда они имеют собственный знак

,

,

.

Образуем скалярное произведение

.

Тогда выражение

(8.9)

называется криволинейным интегралом по координатам, или криволинейным интегралом II рода.

В отличие от криволинейного интеграла I рода, в данном интеграле играет роль направление, заданное на кривой, поэтому будет справедливо свойство

.

Остальные свойства криволинейного интеграла II рода не отличаются от свойств интеграла по мере.

8.2.3. Вычисление криволинейного интеграла по координатам

Рассмотрим, как вычисляется криволинейный интеграл II рода.

1. Пусть кривая L задана параметрически

Подставляя эти соотношения в (8.9), получим

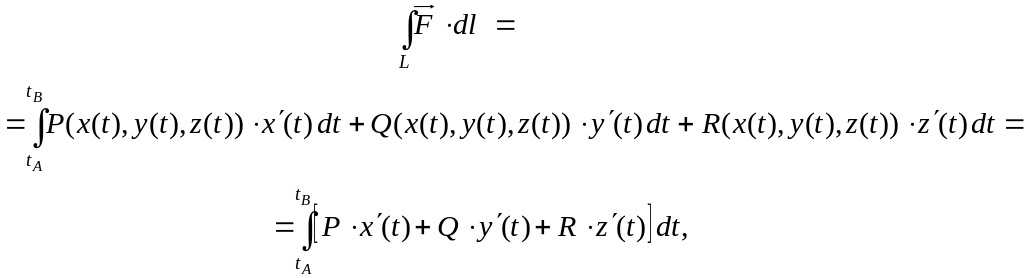
где t_A и t_B − параметры начальной А и конечной В точек интегрирования.

Если кривая L плоская, то формула вычисления упрощается:

.

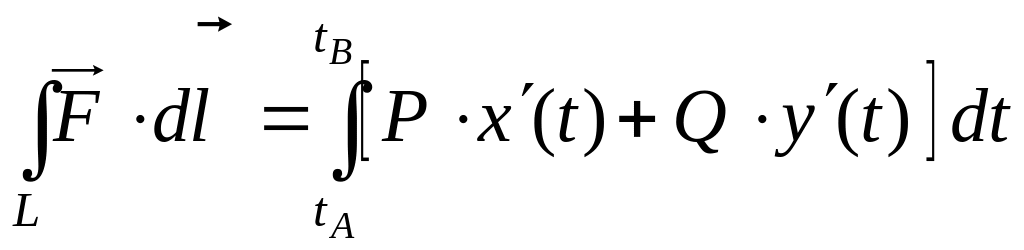2. Пусть кривая L – плоская и задана уравнением 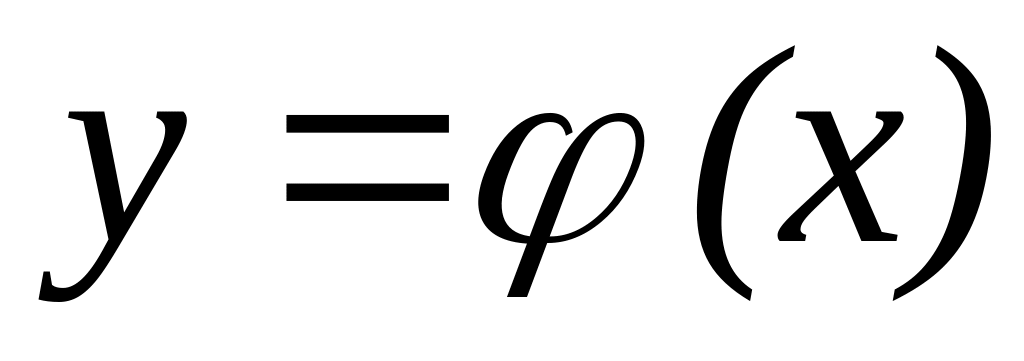. Можно считать, что она задана параметрически, введя промежуточный параметр t

и применить предыдущую формулу для случая плоской кривой, а затем заменить t на х. Получим

.

8.2.4. Формула Грина

Формула Грина устанавливает связь между криволинейным интегралом по границе L плоской области D и двойным интегралом по этой области.

Теорема. Пусть D – правильная область, а функции непрерывны вместе со своими производными и в замкнутой области Тогда имеет место формула Грина

(8.10)

Доказательство

П усть задана область D (рис. 8.8). Рассмотрим интеграл

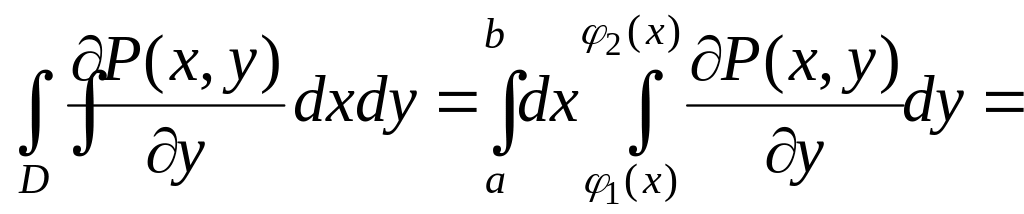
Таким образом,

Аналогично доказывается, что

Из двух последних равенств следует формула (8.10).

Ф ормула Грина справедлива и для двусвязной области D (рис. 8.9), Действительно, область D можно превратить в односвязную, проведя так называемый разрез, т. е. соединив наружный и внутренний контуры некоторой линией и исключив ее из области. При этом двойной интеграл не изменится, а криволинейный интеграл вдоль разреза обращается в нуль, так как разрез при обходе односвязной области проходится в противоположных направлениях.

8.2.5. Независимость криволинейного интеграла от формы кривой интегрирования

Р ассмотрим случай плоской кривой. Две точки А и В – начало и конец пути интегрирования – могут быть соединены различными кривыми: L₁ и L₂ (рис. 8.10).

По каждой из этих кривых, если это возможно, проведем интегрирование. Может случиться, что заданное векторное поле обладает таким свойством, при котором результаты интегрирования не будут зависеть от выбора кривой.

Установим это условие. Пусть

Тогда

т. е. циркуляция Ц = 0 для Справедливы рассуждения и в обратном порядке. Мы пришли к следующему утверждению.

Теорема 1. Для независимости криволинейного интеграла от формы кривой интегрирования необходимо и достаточно, чтобы циркуляция векторного поля была равна нулю по любому замкнутому контуру L.

Это условие неконструктивно. Существует другое условие.

Теорема 2. Для независимости криволинейного интеграла от формы кривой интегрирования необходимо и достаточно, чтобы выражение являлось полным дифференциалом некоторой функции U(x, y), т. е.

.

Доказательство

1.  Достаточность. Пусть 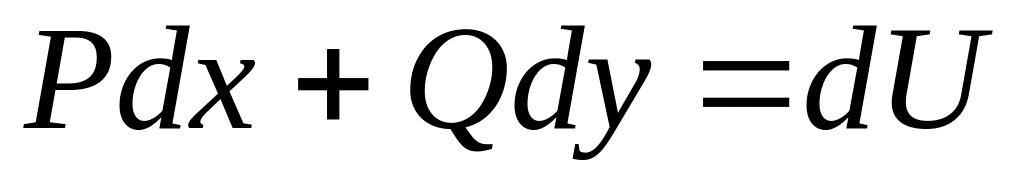, т. е. является полным дифференциалом. Если P и Q − дифференцируемые функции, то

(условие полного дифференциала).

Используя формулу Грина, получим

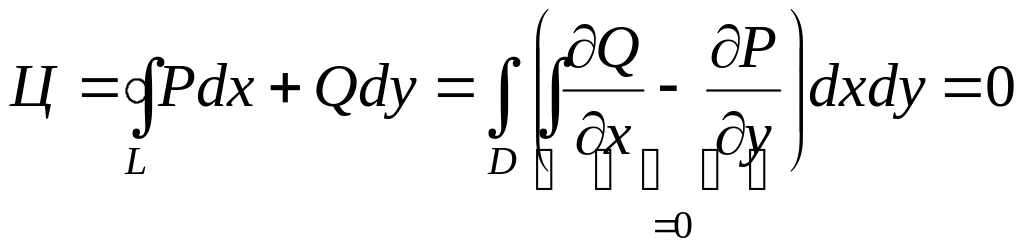, т. е. .

2. Необходимость. Пусть не зависят от L. Это означает, что , т. е.

.

Тогда по формуле Грина

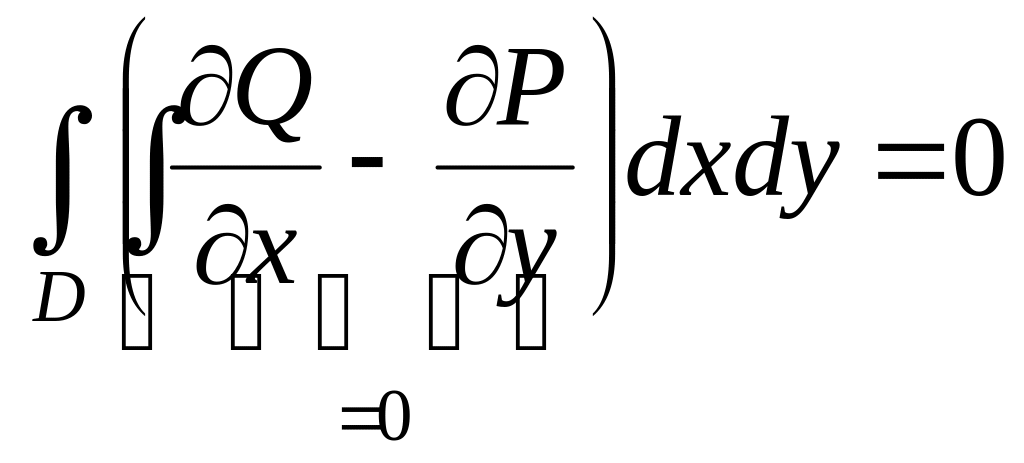, (8.11)

откуда

или .

Замечание. При доказательстве (8.11) использовали лемму:

если и , то f (x,y) = 0.

Из доказанной теоремы вытекает следствие.

Следствие. Если криволинейный интеграл не зависит от формы кривой интегрирования, то

Функцию u(x, y) называют силовой, или потенциальной, а величину – потенциалом.

Тогда

. (8.12)

Вспомним физический смысл скалярного произведения, которое стоит под интегралом в левой части последнего равенства. Это элементарная работа поля на участке кривой L

,

тогда интеграл от этой элементарной работы по кривой L от А до В даст работу поля на кривой АВ. Соотношение (8.12) означает, что работа равна разности потенциалов начала и конца пути и не зависит от формы этого пути.

Заметим теперь, что

,

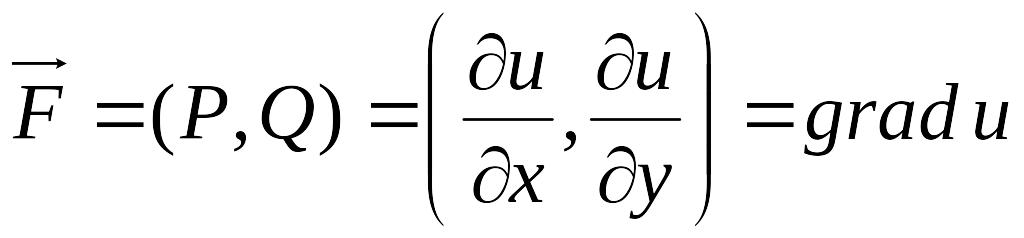т. е. если векторное поле является градиентом некоторого скалярного поля, то криволинейный интеграл не зависит от формы кривой интегрирования. Такие векторные поля называются потенциальными (поле сил тяготения).