
- •1. Неопределенный интеграл
- •1.1. Первообразная и неопределенный интеграл
- •1.2. Основные свойства неопределённого интеграла
- •1.3. Таблица основных интегралов
- •1.4. Замена переменной в неопределенном интеграле. Интегрирование подстановкой
- •1.5. Интегрирование по частям
- •1.6. Интегрирование функций, содержащих квадратный трехчлен
- •1.7. Интегрирование рациональных дробей
- •1.7.1. Интегрирование простейших дробей
- •1.7.2. Интегрирование рациональных дробей с помощью разложения на простейшие дроби
- •1.8. Интегрирование иррациональных функций
- •2. Интегралы вида
- •3. Интегралы вида
- •1.9. Интегрирование тригонометрических функций
- •1. Интегралы вида , где r – рациональная функция
- •2. Интегралы вида
- •5. Тригонометрические подстановки
- •6. Интегралы вида
- •1.10. Функции, интегралы от которых не выражаются через элементарные функции
- •2. Интеграл по мере области
- •2.1. Понятие интеграла по мере области
- •2.2. Основные свойства интеграла по мере области
- •2.3. Вычисление определенного интеграла
- •2.3.1. Формула Ньютона − Лейбница
- •2.3.2. Вычисление определённых интегралов с помощью подстановки
- •2.3.3. Вычисление определённых интегралов путём интегрирования по частям
- •2.4. Приближенное вычисление определённых интегралов. Понятие о численном интегрировании
- •2.4.1. Формула прямоугольников
- •2.4.2. Формула трапеций
- •2.4.3. Формула парабол (Симпсона)
- •3. Несобственные интегралы
- •3.1. Несобственные интегралы с бесконечными пределами интегрирования
- •3.2. Несобственные интегралы от разрывных функций
- •3.3. Теоремы о сходимости несобственных интегралов
- •4. Интеграл как функция пределов интегрирования. Понятие о специальных функциях, определяемых интегралами с переменным верхним пределом
- •5. Понятие об интегралах, зависящих от параметра
- •6. Понятие о гамма-функции
- •7. Вычисление кратных интегралов
- •7.1. Вычисление двойного интеграла в декартовых координатах
- •7.2. Вычисление тройного интеграла в декартовых координатах
- •7.3. Замена переменных в кратных интегралах
- •7.3.1. Общая формула замены переменных
- •7.3.2. Вычисление двойного интеграла в полярных координатах
- •7.3.3. Вычисление тройного интеграла в цилиндрических координатах
- •7.3.4. Запись тройного интеграла в сферической системе координат
- •8. Криволинейные интегралы
- •8.1. Вычисление криволинейного интеграла по длине дуги кривой
- •8.2. Криволинейные интегралы по координатам
- •8.2.1. Понятие о векторном поле
- •8.2.2. Определение криволинейного интеграла по координатам
- •8.2.3. Вычисление криволинейного интеграла по координатам
- •8.2.4. Формула Грина
- •8.2.5. Независимость криволинейного интеграла от формы кривой интегрирования
- •9. Приложения кратных интегралов
- •9.1. Геометрические приложения кратных интегралов
- •9.2. Вычисление геометрических характеристик тел вращения
- •9.2.1. Объём тела с заданным поперечным сечением
- •9.2.2. Объём тела вращения
- •9.2.3. Площадь поверхности вращения
- •9.3. Механические приложения кратных интегралов
- •9.4. Примеры физических приложений определённых интегралов
7.3. Замена переменных в кратных интегралах
7.3.1. Общая формула замены переменных
Рассмотрим в Е3 три семейства поверхностей
![]() (7.5)
(7.5)
Поверхности
![]() называют координатными
поверхностями,
а линии их пересечения – координатными
линиями.
называют координатными
поверхностями,
а линии их пересечения – координатными
линиями.
Тогда
все точки пространства можно задать
тройкой чисел
![]() −
криволинейными координатами точки. А
соотношение (7.5) можно считать формулами
преобразования координат.
Элемент объёма в этой системе координат
тоже криволинейный, и уже нельзя считать,
что он равен произведению трех измерений
−
криволинейными координатами точки. А
соотношение (7.5) можно считать формулами
преобразования координат.
Элемент объёма в этой системе координат
тоже криволинейный, и уже нельзя считать,
что он равен произведению трех измерений
![]()
Если соотношения (7.5) разрешить относительно x, y, z
![]()
то
получим отображение области V
пространства Oxyz
на область V1
пространства
![]() (рис. 7.16). При этом взаимная однозначность
отображений гарантируется условием
(рис. 7.16). При этом взаимная однозначность
отображений гарантируется условием
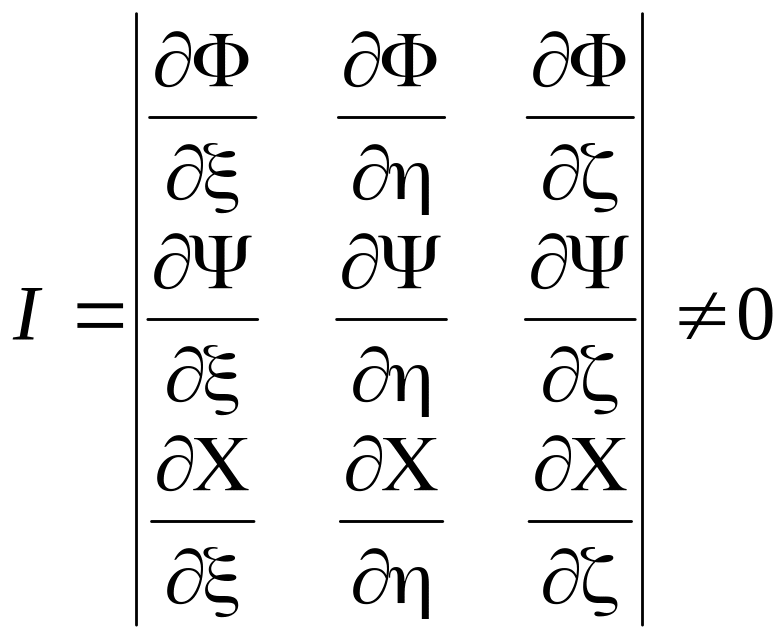 .
(7.6)
.
(7.6)
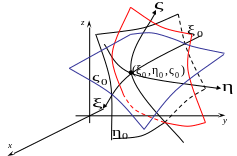
Рис. 7.16
Определитель в (7.6) называется функциональным определителем или Якобианом1. Можно показать, что коэффициент искажения элементарного объёма равен модулю Якобиана, т. е.
![]()
Отсюда для тройного интеграла имеем
![]()
Для двойного интеграла формулы будут выглядеть проще:
формулы преобразования
![]()
Якобиан
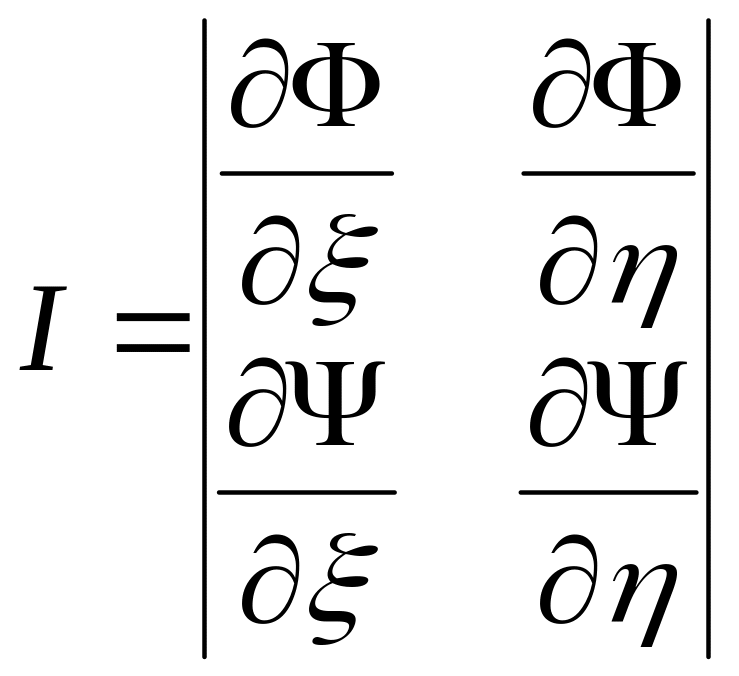 ;
;
формула замены переменных в двойном интеграле
![]() .
.
7.3.2. Вычисление двойного интеграла в полярных координатах
Положение точки М на плоскости можно определить, задав величины:
расстояние r от этой точки до начала координат 0;
у
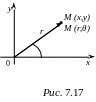 гол
гол
 между радиусом-вектором
между радиусом-вектором
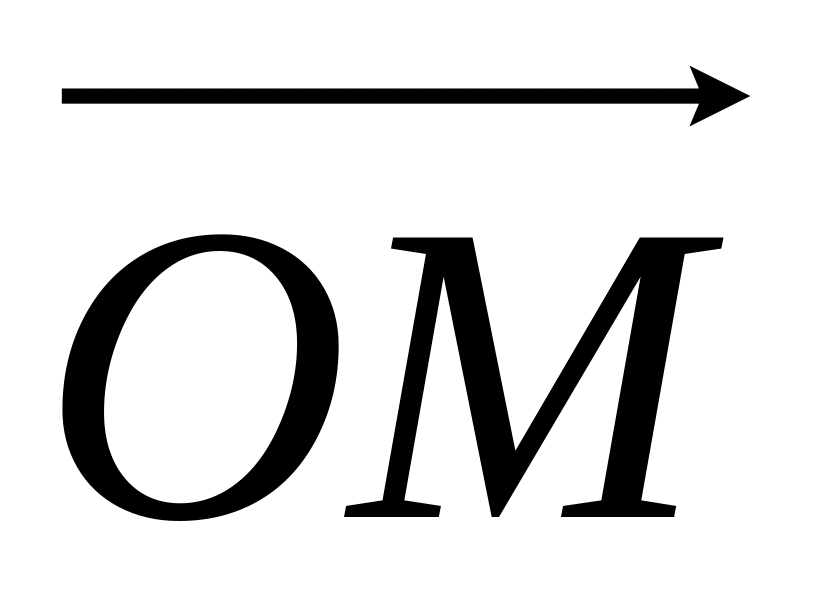 и осью Ox
(рис. 7.17).
и осью Ox
(рис. 7.17).
При
этом считают, что
![]() .
.
Упорядоченная
пара чисел (r,![]() называется
полярными
координатами
точки М. Связь
с декартовыми координатами осуществляется
при помощи формул
называется
полярными
координатами
точки М. Связь
с декартовыми координатами осуществляется
при помощи формул
![]()
Якобиан
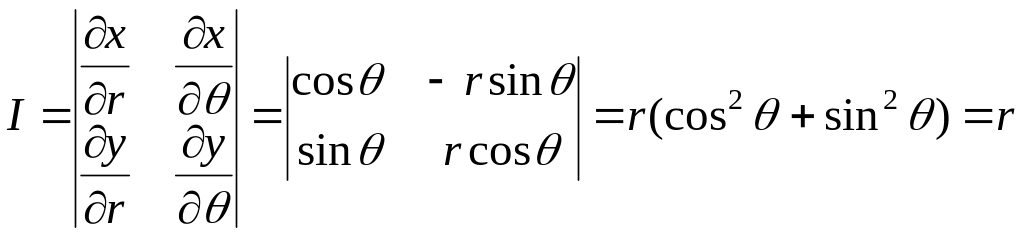 .
.
Тогда двойной интеграл в полярных координатах
![]() .
.
7.3.3. Вычисление тройного интеграла в цилиндрических координатах
Положение любой точки М в пространстве можно определить, задав три величины:
расстояние r от этой точки до оси Oz;
угол θ между координатной плоскостью Oxz и плоскостью, проходящей через точку М и ось Oz;
расстояние z от точки М до координатной плоскости Oxy (рис. 7.20).
П
 ри
этом предполагается, что
ри
этом предполагается, что
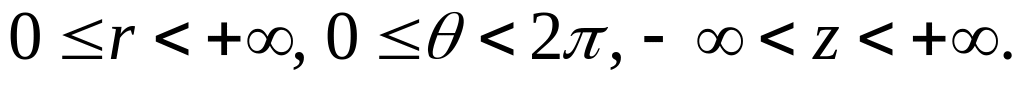
Упорядоченная
тройка чисел (![]() называется цилиндрическими
координатами
точки М,
которые связаны с декартовыми координатами
соотношениями:
называется цилиндрическими
координатами
точки М,
которые связаны с декартовыми координатами
соотношениями:
![]()
Цилиндрическая
система координат является ортогональной
(ортогональны касательные плоскости к
координатным поверхностям
![]() Координатными поверхностями здесь
являются поверхности:
Координатными поверхностями здесь
являются поверхности:
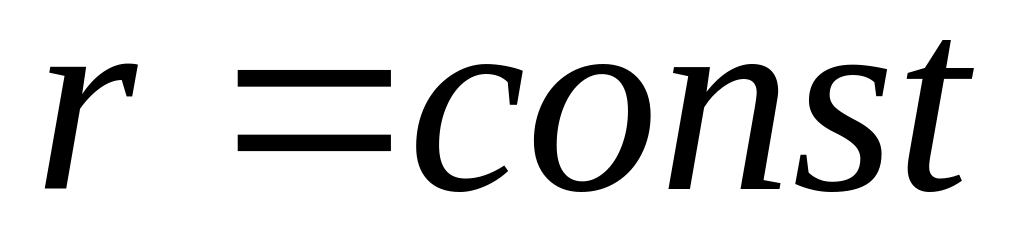 – цилиндрическая
поверхность;
– цилиндрическая
поверхность;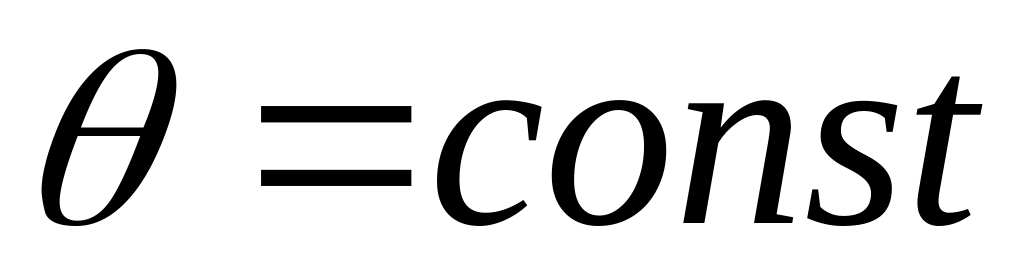 – плоскости,
проходящие через ось Oz;
– плоскости,
проходящие через ось Oz; – плоскости,
перпендикулярные оси Oz.
– плоскости,
перпендикулярные оси Oz.
Якобиан отображения в цилиндрическую систему имеет вид
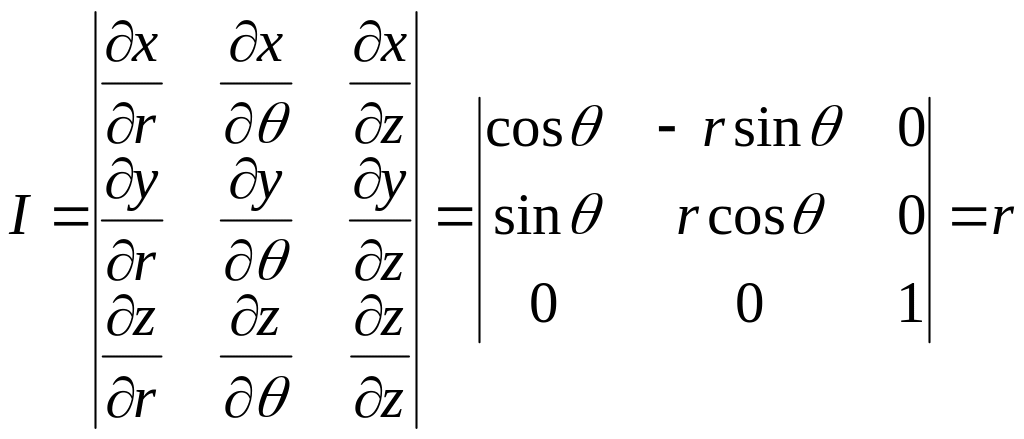 .
.
Тогда запись тройного интеграла в цилиндрических координатах
![]()
7.3.4. Запись тройного интеграла в сферической системе координат
Положение точки М в пространстве можно определить, задав три величины:
р
 асстояние
r
от этой точки до начала координат 0;
асстояние
r
от этой точки до начала координат 0;угол между координатной плоскостью Oxz и плоскостью, проходящей через точку М и ось Oz;
угол
 между радиусом-вектором
и осью Oz
(рис. 7.24).
между радиусом-вектором
и осью Oz
(рис. 7.24).
При
этом считают, что
![]()
Упорядоченная
тройка чисел (r,![]() называется
сферическими
координатами
точки М. Связь
с декартовыми координатами осуществляется
при помощи формул
называется
сферическими
координатами
точки М. Связь
с декартовыми координатами осуществляется
при помощи формул
![]()
Сферические координаты тоже являются ортогональными. Координатными поверхностями здесь являются
− сфера радиуса r;
− плоскость, проходящая через ось Oz;
 − коническая
поверхность с углом при вершине
− коническая
поверхность с углом при вершине
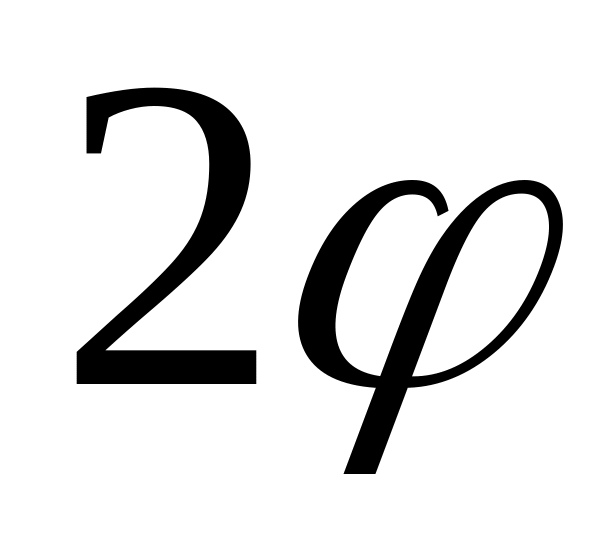 и с осью, совпадающей с Oz.
и с осью, совпадающей с Oz.
Якобиан отображения из декартовой в сферическую систему координат
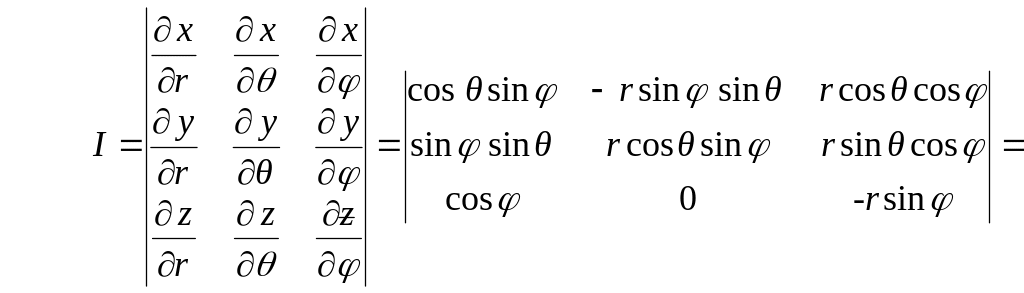
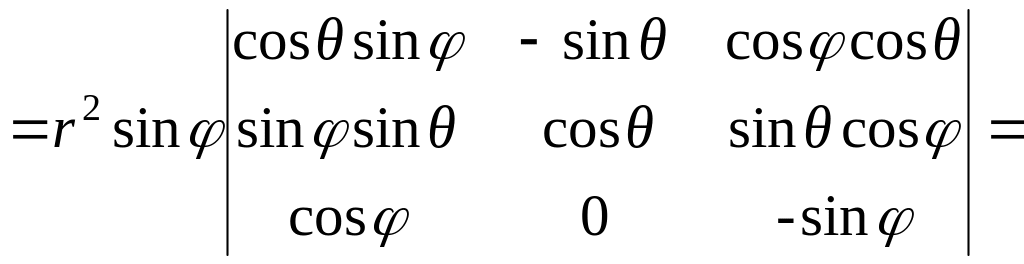
![]()
![]()
Поэтому тройной интеграл в сферических координатах записывают в виде
![]()
