2.1. Понятие интеграла по мере области

При решении многих задач физики, техники, математики требуется вычислить какие-то суммарные характеристики рассматриваемого объекта или процесса (часто говорят: «интегральные характеристики»). При этом характеристики объекта или процесса могут быть переменными: говорят, что локальные характеристики переменны и зависят от координат, времени. К таким задачам относятся, например, задачи отыскания площади, объема тел различной конфигурации, массы, моментов инерции тел, материал которых имеет различную плотность в различных точках, нахождения пути, пройденного материальной точкой при движении с изменяющейся скоростью, и т. д.

При решении таких задач используется общая математическая модель – интеграл по мере (или «интеграл по фигуре»).

Рассмотрим, как решается задача об отыскании массы тела, плотность которого в каждой точке известна и различна. Этим телом (фигурой) может быть:

1. прямолинейный стержень – l;

2. криволинейный стержень – L;

3. плоская пластина любой формы – D;

4. криволинейная поверхность – G;

5. тело, ограниченное любыми поверхностями, – V.

Чтобы обобщить эти объекты, будем говорить о фигуре G, обладающей некоторой массой. Пусть известна плотность распределения массы этой фигуры в каждой её точке Р

.

Так как масса – величина положительная, то необходимо считать эту функцию непрерывной и положительной на G.

Вычислим массу такой фигуры.

1. Разобьем фигуру G произвольным образом на непересекающиеся части . Заметим, что при таком делении мы используем метрическую характеристику:

• в 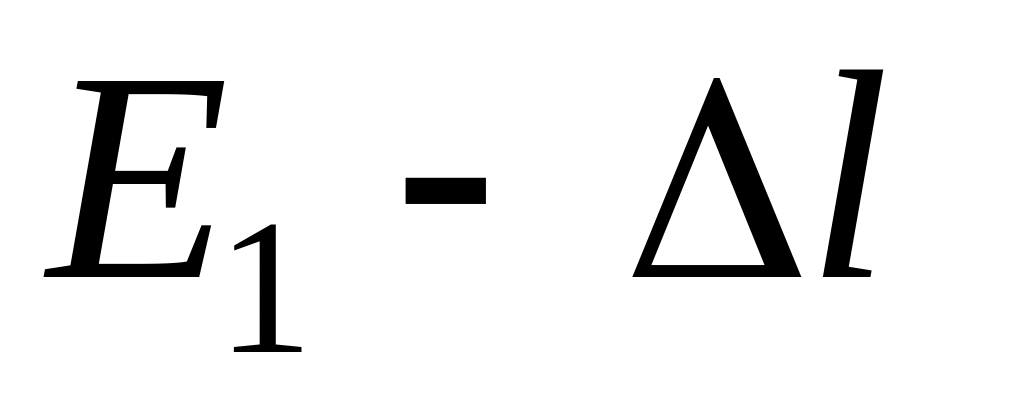– длина;

• в 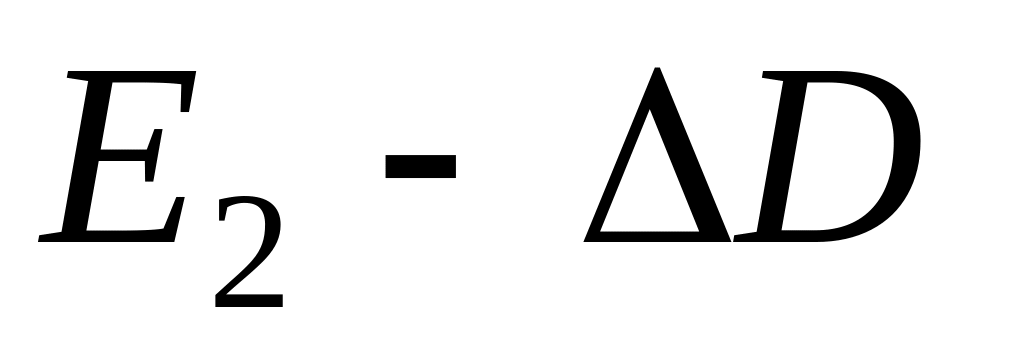– площадь;

• в 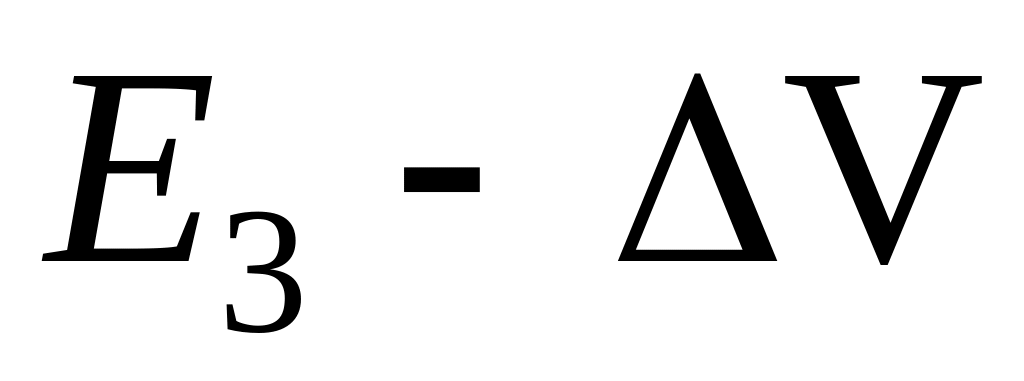– объем.

Будем обозначать эту характеристику и назовём её мерой.

Меру можно представить как функцию множества

,

т. е. множество отображается на множество действительных чисел.

Основные свойства меры:

а) неотрицательность

;

б) аддитивность

,

предполагается, что .

2. В каждой части выберем произвольную точку P_i и предположим, что плотность массы постоянна в пределах и равна её значению в точке P_i, т. е. .

3. Определим приближенное значение массы части

.

4. Масса (приближение) всей фигуры ищется суммированием частичных масс

.

Выражение, стоящее справа, называется интегральной суммой.

5. Для нахождения точного значения массы переходим к пределу, устремив к нулю наибольший из диаметров частей . Обозначим его :

.

Тогда

.

Заметим, что при .

Если теперь отвлечься от конкретной задачи поиска массы, то можно составить интегральную сумму для некоторой непрерывной функции f(P), заданной на замкнутой, ограниченной фигуре G (можно говорить о замкнутой, ограниченной области, множестве). Это выражение вида

.

Рассмотрим предел этих интегральных сумм при Если этот предел не зависит ни от способа разбиения фигуры на части , ни от выбора точек P_i в каждой из частей, то его называют интегралом по мере (по фигуре) от функции f(P) и обозначают

. (2.1)

К онкретизируем введенные понятия для различных фигур.

I. Для отрезка [a, b] оси 0х (отрезок прямолинейного стержня, рис. 2.1)

(2.2)

− это обычный определенный интеграл.

Если − линейная плотность материала стержня, то (2.2) выражает его массу.

II. Для пространственной кривой l (рис. 2.2), т. е. G – это часть кривой, интеграл (2.1) принимает вид

. (2.3)

Если – функция линейной плотности массы, то (2.3) определяет массу криволинейного стержня.

Для плоской кривой выражение (2.3) немного упрощается:

. (2.4)

Интегралы (2.3) и (2.4) называются криволинейными интегралами по длине дуги, или криволинейными интегралами I рода.

III. В пространстве R² в качестве фигуры имеем ограниченную часть плоскости – область D (рис. 2.3). Тогда

, .

Интеграл (2.1) принимает вид

, (2.5)

где d_i – диаметр .

Интеграл (2.5) называется двойным интегралом по области D.

Если – функция плотности массы, то (2.5) выражает массу неоднородной пластины.

IV. Для поверхности Q, где

, ,

интеграл (2.1) принимает вид

(2.6)

и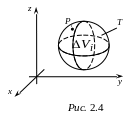 называется поверхностным интегралом по площади поверхности.

Если – функция поверхностной плотности массы, то (2.6) выражает массу поверхности Q.

V. Для пространственного тела Т (рис. 2.4), где

, ,

интеграл (2.1) принимает вид

(2.7)

и называется тройным интегралом по области Т.

Если − функция объемной плотности массы, то (2.7) выражает массу тела Т.