
Точно Не проект 2 / Не books / Источник_1
.pdf60 |
Глава 2 |
|
|
n3 и от n2 к n3, получим L3={1,3,5}. Затем соответствующие ограничения распространяются в обратную сторону. При этом множества L2 и L1 не изменяются. Наконец, аналогичные операции выполняются с вершиной n4. В итоге L4={3,4}, L2={4,5}, L3={3,5}. Затем ограничения распространяются между n2 и n3 (это дает L3={3}), а также от n2 и n3 к n1. Получаем L1={3,4}. Распространяя ограничения обратно от n1 к n2, n3 и n4, получаем окончательный результат: l1=4, l2=4, l3=3, l3=2. Распространение ограничений продолжается до тех пор, пока на множествах меток происходят изменения.
Вобщем случае вершина может иметь несколько меток. При этом произвольно комбинировать метки для разных вершин нельзя. Необходимо учитывать существующие ограничения. Очевидно, в этом случае задача имеет несколько решений.
Вглаве 10 рассмотрено применение метода распространения ограничений для решения задачи интерпретации контурных рисунков трехмерных тел (алгоритм Хаффмана-Клоуза).
2.3. Поиск решений при сведении задач к подзадачам
При таком представлении задачи поиск решений выполняется с использованием И-ИЛИ графов. Рассмотрим особенности поиска в И-ИЛИ графах в сравнении с поиском в пространстве состояний.
Впространстве состояний решение представляет путь из начальной вершины в целевую вершину. Решение в И-ИЛИ графах соответствует подграфу или поддереву, так как при раскрытии И-вершины необходимо определить, являются ли разрешимыми все ее дочерние вершины. Наличие ИЛИ-вершины приводит к тому, что в ходе поиска решения рассматривают несколько возможных подграфов решений. Если необходимо найти оптимальный граф решений, то вводятся оценочные функции. Однако, в отличие от поиска в пространстве состояний, эти функции представляют не стоимости путей, а стоимости графов, в частности, графа решения или его подграфов.
Впроцессе поиска строятся подграфы, которые выступают в роли претендентов на участие в формировании полного графа решения. Будем называть такие подграфы потенциальными подграфами решений. Обычно
входе поиска строятся несколько потенциальных подграфов, которые определенным образом представляются в памяти ЭВМ. Построение указанных подграфов выполняют повторением двух обобщенных действий:
а) определяют, являются ли вершины потенциального подграфа решения разрешимыми, неразрешимыми (тупиковыми) или нераскрытыми; если необходимо, то вычисляют стоимости соответствующих подграфов;
Способы представления задач и поиск решений |
61 |
|
|
б) расширяют потенциальный подграф решений.
Входе выполнения первого действия проверяют все концевые вершины потенциального подграфа. Если эти вершины соответствуют элементарным задачам, решение которых известно, то они считаются заключительными и помечаются меткой SOLVED (разрешимые). Если концевые вершины являются тупиковыми, то они помечаются как неразрешимые (метка UNSOLVED). Затем анализируются их родительские вершины. Родительская И-вершина помечается как разрешимая, если разрешимыми являются все ее дочерние вершины, иначе она помечается как неразрешимая. Родительская ИЛИ-вершина получает метку, совпадающую с меткой дочерней вершины, рассматриваемой в данный момент.
Если начальная вершина потенциального подграфа решений помечается как разрешимая, то данный потенциальный подграф становится возможным подграфом решения.
Вслучае поиска оптимального графа решения оценивается стоимость всех вершин потенциальных подграфов решений, начиная с концевых вершин. Правила указанных вычислений будут рассмотрены ниже.
При выполнении второго действия раскрывают концевые вершины потенциального подграфа решений, которые не имеют меток. Если раскрываемая концевая вершина является И-вершиной, то генерируется новый потенциальный подграф путем добавления всех дочерних вершин к расширяемому потенциальному подграфу. Если раскрываемая концевая вершина
–это ИЛИ-вершина, то к расширяемому потенциальному подграфу добавляется только одна дочерняя вершина. При этом формируется столько потенциальных подграфов, сколько имеется вершин.
Аналогично поиску в пространстве состояний при поиске в пространстве редукции задачи выделяют алгоритмы слепого и упорядоченного (эвристического) поиска.
2.3.1.Алгоритм поиска в глубину
Врассматриваемом ниже алгоритме элементами списка OPEN являются потенциальные подграфы решений, т.е. подграфы, начальная вершина которых не имеет метки или имеет метку SOLVED (подграф решения). В процессе поиска вновь формируемые потенциальные подграфы решений помещаются в начало списка OPEN.
Procedure Depth_First_AO1;
Begin
Поместить в список OPEN потенциальный подграф, состоящий только из начальной вершины S;
Выполнить разметку данного подграфа;
62 |
Глава 2 |
|
|
While OPEN <> 'пустой список' Do
Begin
P:= first (OPEN); {выбрать из OPEN первый подграф}
{применить к подграфу P функцию проверки разрешимости solved(P) }
IF solved(P) THEN выход ('УСПЕХ');
Удалить подграф P из списка OPEN;
Расширить подграф P и выполнить разметку вновь сформированных потенциальных подграфов решений;
Поместить все новые потенциальные подграфы решений в на-
чало списка OPEN;
End;
Выход ('НЕУДАЧА')
End.
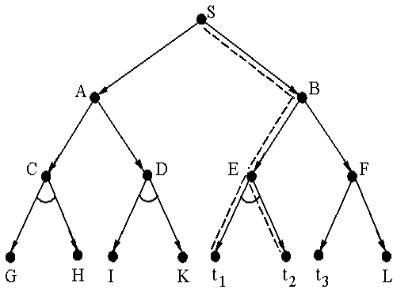
Рассмотрим применение процедуры к графу редукции, изображенному на рисунке 2.11. Здесь концевые вершины, отмеченные прописными буквами, соответствуют неразрешимым задачам, а вершины, отмеченные строчными буквами, являются заключительными (терминальными).
Рисунок 2.11—Граф редукции задачи
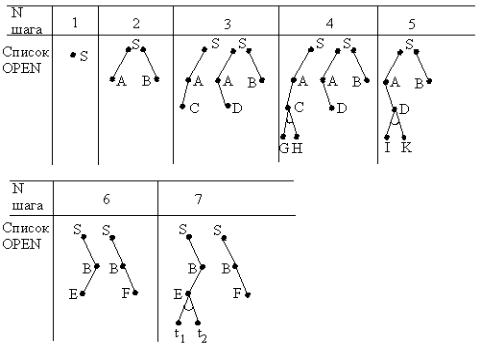
На рисунке 2.12 представлены потенциальные подграфы решений, помещаемые в список OPEN на разных шагах выполняемой процедуры. На шаге 4 расширяемый потенциальный подграф решений помечается как неразрешимый и из дальнейшего рассмотрения исключается. Аналогичная ситуация имеет место на шаге 5. В дальнейшем расширяется правый подграф вершины S, который и приводит к графу решения, показанному на рисунке 2.11 штриховой линией.
Способы представления задач и поиск решений |
63 |
|
|
Рисунок 2.12 – Потенциальные графы решений при поиске в глубину
В рассматриваемом примере в списке OPEN хранятся несколько потенциальных подграфов решений. Если граф редукции задачи является сложным, то это приводит к неэффективному использованию памяти ЭВМ. Для устранения указанного недостатка, необходимо при раскрытии очередной вершины потенциального подграфа решения рассматривать не все дочерние вершины, а только одну. С этой целью в процедуру поиска вводится функция NextChild [86].
Пусть у вершины n имеются дочерние вершины n1,n2,…,ni,…,nm и вершина ni уже включена в потенциальный граф решения. Тогда функция NextChild определится следующим образом
ni 1,0 i m,
NextChild (n)
nil,i m,
где i=0 до применения функции к вершине n. В этом случае процедуру поиска в глубину можно переписать в виде:
Procedure Depth_first_AO2; Begin
Создать потенциальный подграф P, состоящий только из одной начальной вершины S;
n:=S;
Выполнить разметку подграфа P;
64 |
Глава 2 |
|
|
While True Do Begin
If unsolved (P) Then выход ('НЕУДАЧА'); If solved (P) Then выход ('УСПЕХ');
If n не имеет метки Then
Begin n:=NextChild(n);
Построить новый потенциальный подграф решения,
добавив в P вершину n;
Выполнить разметку нового потенциального подграфа и обозначить его через P;
End
Else
Begin
If n имеет метку UNSOLVED Then
Удалить вершину n из подграфа P; n:=родительская вершина (n)
End
End
End.
Если данную процедуру применить к дереву редукции задачи, изображенному на рисунке 2.11, то порядок обработки вершин будет следую-
щим: S, A, C, G(UNSOLVED), C(UNSOLVED), A, D, I(UNSOLVED), D(UNSOLVED), A(UNSOLVED), S, B, E, t1(SOLVED), E, t2(SOLVED), E(SOLVED), B(SOLVED), S(SOLVED).
Когда вершина помечается меткой UNSOLVED, то она исключается из потенциального подграфа решения. В итоге в подграф решения включаются только вершины, помеченные меткой SOLVED.
Каждый раз, когда обнаружена неразрешимая вершина, процедура выполняет возврат к родительской вершине, обеспечивая обследование других альтернативных ветвей графа редукции задачи. Если обнаружена разрешимая вершина и при этом еще не законченно построение подграфа решения, то возврат выполняется с целью обследования оставшихся конъюнктивных ветвей. Благодаря возврату нет необходимости раскрывать все дочерние вершины одновременно и запоминать альтернативные потенциальные подграфы решений.
2.3.2. Алгоритм эвристического поиска в И-ИЛИ графе
Алгоритмы эвристического поиска предполагают упорядочение списка OPEN в соответствии с некоторой эвристической оценочной функцией. При поиске в пространстве состояний эвристическая функция представляла собой оценку стоимости пути между текущей и целевой верши-
Способы представления задач и поиск решений |
65 |
|
|
нами. В случае поиска в И-ИЛИ графе эвристическая функция соответствует оценке стоимости подграфа решения.
Обозначим через h(n) стоимость подграфа решения, начинающегося в вершине n. Стоимость подграфа решения определяется рекурсивно:
а) если n соответствует заключительной вершине, то h(n)=0; б) для любой другой вершины
k
h(n) [h(ni ) c(n,ni )],
i 1
где ni, i=1,2,…,k – дочерние вершины для вершины n; c(n,ni) – стоимость дуги между вершинами n и ni. Определение стоимости подграфа решения начинается с заключительных вершин и заканчивается начальной вершиной.
В ходе поиска подграфа решения рассматриваются потенциальные подграфы решений, для которых концевые вершины – это, как правило, еще нераскрытые вершины. Для определения стоимости потенциальных
подграфов решений вводятся оценки h(n), обозначаемые hˆ(n) . При этом hˆ(n) 0, если n – заключительная вершина, и
k |
|
hˆ(n) [hˆ(ni ) c(n,ni )] , |
(2.3) |
i 1
где n – рассматриваемая вершина. Оценка hˆ(n) строится на основе эвристической информации.
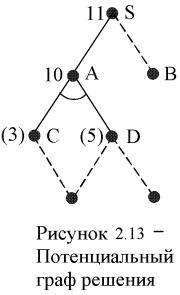
Рассмотрим пример. На рисунке 2.13 изображен потенциальный граф решения. Здесь пунктирными линиями показаны не построенные ветви. Цифры в скобках рядом с вершинами C и D обозначают эвристические оценки подграфов решений, начинающихся в этих вершинах. Цифры без скобок (вершины A, S) обозначают оценки, вычисляемые в соответствии с формулой (2.3).
Стоимость дуги полагается равной единице.
При известных эвристических оценках подграфов решений, начинающихся в вершинах С и D, оценка подграфа для вершины А равна
hˆ(A) hˆ(C) c(A,C) hˆ(D) c(A,D) 10
,
а полная оценка стоимости hˆ(S) изображенного потенциального графа равна 11.
66 |
Глава 2 |
|
|
Эвристический алгоритм упорядоченного поиска можно представить в виде процедуры:
Procedure AO_Search;
Begin
Поместить в список OPEN потенциальный граф P, состоящий
только из начальной вершины S;
Выполнить разметку графа P;
Вычислить оценку hˆ(S) ;
While OPEN <> ' пустой список' Do
Begin
P:=first(OPEN);{выбрать из OPEN первый граф}
If solved(P) Then выход ('УСПЕХ');
Удалить граф P из списка OPEN;
Расширить граф P, выполнить разметку всех вновь сформированных потенциальных графов Pi , определить оценки hˆ(Pi ) ;
Внести потенциальные графы Pi в список OPEN c учетом
оценок hˆ(Pi )
End
Выход ('НЕУДАЧА')
End.
В рассматриваемой процедуре используется определенный порядок раскрытия вершин. Если раскрываемая вершина n является дизъюнктивной, то в новый потенциальный подграф решения включается только одна ее дочерняя вершина. Если раскрываемая вершина конъюнктивная, то в новый потенциальный подграф решения включаются все ее дочерние вершины. В дальнейшем, в первую очередь, раскрывается та из дочерних
вершин, которая имеет максимальную оценку hˆ(ni ). Основанием такого выбора является то, что необходимо как можно скорее выяснить, разрешима или не разрешима родительская И-вершина n. И-вершина неразрешима, если неразрешима хотя бы одна из ее дочерних вершин. Если этот факт будет установлен, то подграф потенциального графа решений, начинающихся в вершине n, из дальнейшего рассмотрения исключается. Вероятность обнаружения неразрешимости И-вершины повышается, если двигаться в на-
правлении максимальной оценки hˆ(ni ).
Рассмотрим применение процедуры эвристического поиска к графу редукции задачи, изображенному на рисунке 2.14. На рисунке 2.15 показаны потенциальные графы решений, хранящиеся в списке OPEN. На шаге 3
раскрывается вершина B, имеющая оценку hˆ(B) 5. Раскрытие вершины B
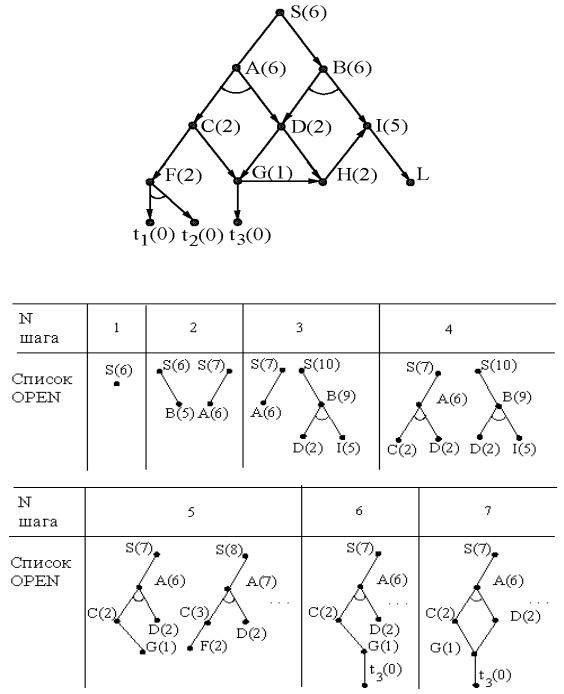
Способы представления задач и поиск решений |
67 |
|
|
приводит к подзадачам D и I с оценками 2 и 5. В результате этого рассматриваемый потенциальный подграф получает оценку 10 и переводится на второе место списка OPEN. В дальнейшем строится левый подграф вершины S и на шаге 7 потенциальный граф помечается как граф решения.
Рисунок 2.14 – Граф редукции задачи с оценками hˆ(n )
Рисунок 2.15 – Потенциальные подграфы решений
Аналогично поиску в глубину в рассматриваемую процедуру можно включить функцию NextChild(n). Это позволит повысить эффективность
68 |
Глава 2 |
|
|
использования памяти ЭВМ при поиске в графах редукции задач с большим числом вершин.
Если алгоритм поиска находит оптимальный граф решения (такой граф имеет минимально возможную оценку hˆ(s) ), то он называется гарантирующим. Можно показать, что алгоритм поиска в И-ИЛИ графе будет гарантирующим, если hˆ(n) h(n) и стоимости всех дуг c(n,ni ) больше некоторой положительной величины [86].
Если положить стоимость всех дуг равной нулю, то будут минимизироваться только предстоящие затраты.
2.3.3.Поиск решений в игровых программах
Всложных играх, например шахматах, лучшие игроки (люди) в большинстве случаев все еще превосходят компьютерные программы. Пока не существует принципов построения программ, позволяющих компьютерам выиграть шахматную партию наверняка. В то же время игра в шахматы с помощью компьютера представляет собой проблему, которой в ИИ уделяется большое внимание. Прогресс в этой области оценивается как прогресс в ИИ. Помимо шахмат, большое внимание в ИИ уделялось шашкам, игре “го”, различным вариантам игры в крестики-нолики и др. [55]
Все эти игры характеризуются как игры с полной информацией о текущей игровой ситуации (имеются игры с неполной информацией), где два игрока-противника по очереди делают ходы. Успех одного игрока – такая же по величине потеря для другого игрока (игры с нулевыми суммами). Допустимые ходы игры определяются конечным набором правил, которые исключают случайность. Игра начинается из специфического начального положения и завершается победой того или иного игрока, либо ничьей. При рассмотрении игровых программ игроком считается компьютер, а противником – человек .
Сложность поиска решений в игровых деревьях весьма высока, так как вершины имеют высокую степень разветвления. Например, в середине шахматной партии игрок может сделать около 35 ходов, разрешенных пра-
вилами. Общее количество вершин дерева игры в шахматы оценивается значением 10120. Это число сравнимо с числом молекул во Вселенной или
количеством наносекунд, прошедших от момента “Большого взрыва”. Если предположить, что можно обследовать 109 вершин в секунду, то построение полного дерева игры в шахматы заняло бы 10103 лет [77]. Из этого следует, что полный просмотр такого дерева невозможен. Поэтому при поиске
вигровых деревьях необходимо выполнять следующее:
1) прогнозировать граничную глубину поиска;
Способы представления задач и поиск решений |
69 |
|
|
2) оценивать перспективность позиций игры с помощью эвристических функций.
Для этого в каждой позиции игры формируется дерево возможных продолжений игры, имеющее определенную глубину, и с помощью эвристической оценочной функции вычисляются оценки концевых вершин такого дерева. Затем полученные оценки распространяются вверх по дереву, и корневая вершина, соответствующая текущей позиции, получает оценку, позволяющую выяснить силу игрока в данной позиции. При игре в шахматы современные компьютерные программы просматривают возможные продолжения игры примерно на 10 ходов вперед. Основная идея такого оценивания заключается в том, что просмотр возможных продолжений игры из заданной позиции на определенную глубину позволяет точнее оценить перспективность того или хода.
2.3.3.1. Минимаксный метод. В соответствии с минимаксным методом вместо полного просмотра дерева игры обследуется лишь его небольшая часть. В этом случае говорят, что дерево подвергается подрезке. Простейший способ подрезки — это просмотр дерева игры на определенную глубину. Это означает, что процесс обследования заканчивается в вершинах, которые не являются терминальными (концевыми). Поэтому дерево поиска – это только верхняя часть дерева игры. Для оценки силы игрока в различных позициях поискового дерева применяются оценочные функции. Причем, чем выше оценка в соответствующей позиции, тем больше шансов на выигрыш у игрока, а чем ниже оценка, тем выигрышнее позиция противника. Поэтому игрок стремится максимально увеличить выигрыш, а противник – минимизировать проигрыш. Обычно в алгоритмах позиции игрока обозначают через МАКС (МАХ), а позиции противника – через МИН (MIN).
Различают два вида оценок: статические и динамические. Статические оценки приписываются концевым вершинам дерева поиска и вычисляются на основе эвристических правил. При игре в шахматы эти правила учитывают перевес фигур, контроль центра, подвижность фигур и пр. Динамические оценки получаются при распространении статических оценок вверх по дереву. Метод, которым это достигается, называется минимаксным. Заключается он в следующем. Для вершины, в которой ход выполняет игрок (МАКС), выбирается наибольшая из оценок вершин нижнего уровня (т.е. уровня МИН'а). Это абсолютно оправдано, так как в этом случае игрок сделает для себя наиболее выгодный ход. Для вершины, в которой ход выполняет противник, выбирается наименьшая из оценок дочерних вершин, так как противник стремится сделать ход наименее выгодный игроку. На рисунке 2.16 показан пример распространения статических оценок вверх по поисковому дереву в соответствии с указанным минимаксным
