
Точно Не проект 2 / Не books / Источник_1
.pdf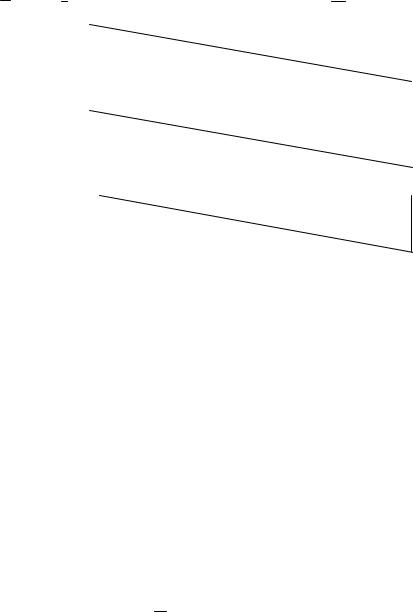
150 |
Глава 4 |
|
|
S(y) I(x, y) R(x, y) |
|
|
|
|
R (nil , y) R(nil , y) |
|||
|
|
|
1 {nil/ x} |
|
||||
S(nil) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
( y) I |
(nil , y) R(nil , y) |
||||||
|
|
|
2 {nil/ y} |
|
||||
I(nil,nil) |
|
|
|
|
|
|
||
|
|
|
|
(nil , nil ) R(nil , nil ) |
||||
|
|
I |
||||||
R(nil,nil)
Рисунок 4.8 – Модифицированное дерево доказательства для yR(nil, y)
Чтобы выполнить доказательство для случая n>0 , сформулируем новое дополнительное индуктивное утверждение: “для любого непустого списка х его хвост, получаемый с помощью функции cdr(x), можно отсортировать“. Если допустить, что у нас уже есть функция sort, которая может выполнить сортировку списка, то указанное утверждение можно записать в виде дизъюнкта R(cdr(x),sort(x)). Добавим его к множеству аксиом Ф0. Также добавим к множеству Ф0 очевидное предложение
R(cons(car(x),cdr(x)), y) R(x, y),
которое после исключения знака импликации примет вид
R(cons(car(x),cdr(x)), y) R(x, y).
Если учесть, что cons(car(x), cdr (x))=x, то последнее предложение представляет собой тавтологию, и ее добавление не создает противоречия.
Модифицированное дерево доказательства для предположенияx yR(x, y)изображено на рисунке 4.9.
Заменив в ответном утверждении функцию а на переменную х, полу-
чим
R(x, merge(car(x),sort(cdr(x)))).
Объединяя результаты доказательства для n=0 и n>0, получаем рекурсивную программу упорядочения списка чисел:

Основные модели вывода |
|
151 |
|
|
|
|
|
|
nil, |
если x nil, |
|
sort(x) |
|
|
в ином случае. |
merge(car(x),sort(cdr(x))) |
|||
R(cons(car(x),cdr(x)), y) R(x, y) |
|
R (a , y ) R (a , y ) |
|
|
|
1 {a/x} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R(cons(car(a),cdr(a)), y) R(a, y) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
(y) I |
(x,y) R(x,y) |
|
|
|
|
2 {cons(car(a),cdr(a))/ x} |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
(y) I |
(cons(car(a),cdr(a)),y) R(a, y) |
||
|
|
(x, y) I(cons (u, x),merge (u, y)) |
|
|
3 {car(a)/u,cdr(a)/ x, |
|
|||||||||||||||||||||||
I |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
merge(cdr(a), y)/ y} |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
(cdr(a), y) S(merge(car(a), y)) R(a,merge(car(a), y)) |
|||||||||||||||
|
|
|
|
|
|
I(x, y) |
|
|
(x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
4 {cdr(a)/ x} |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
(cdr(a), y) S |
(merge (car (a), y)) R(a,merge (car(a), y)) |
|||||||||||||||||
|
|
|
|
|
|
(y) S(merge (x, y)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 {car(a)/ x} |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
( y) |
R |
(cdr (a), y) R(a,merge (car (a), y)) |
||||||||||
|
|
|
|
|
|
R(x, y) S(y) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
R(cdr(a), y) R(a,merge(car(a), y))
R(cdr(x),sort(cdr(x)))
6 {a/ x,sort(cdr(a))/ y}
R(a,merge(car(a),sort(cdr(a)))
Рисунок 4.9 – Модифицированное дерево доказательства для x yR(x,y)
152 |
Глава 4 |
|
|
4.1.7. Принцип резолюции и система STRIPS
Система STRIPS (от англ. Stanford Research Institute Problem Solver –
решатель задач Стэнфордского исследовательского института) относится к классу решателей задач и представляет собой программу управления роботом, который способен целенаправленно передвигаться в среде с подвижными препятствиями [44]. Задачу перемещения (навигации) робота можно рассматривать как задачу поиска в пространстве состояний. Описание задачи состоит из:
-описания состояния (модели) среды, в которой находится робот;
-описания набора имеющихся операторов, каждый из которых преобразует модель среды;
-описания целевого состояния.
Пространство состояний описывается множеством ППФ. Например, состояние, при котором робот находится в точке а, а контейнеры k1 и k2 -- в точках b, c, d , можно описать с помощью следующих ППФ:
ATR(a);
AT(k1,b);
AT(k2,c);
AT(k3,d).
Операторы представляются в виде операторных схем, которые характеризуются именем, списком параметров и описаниями. Описания операторных схем выполняются на языке исчисления предикатов и включают в себя условия применимости оператора, список вычеркиваний и список добавлений. Например, операторная схема goto(m,n) определяет обобщенное действие, связанное с переходом робота из точки m в точку n. Переменные m и n рассматриваются как параметры схемы, в которые подставляются константы, задающие возможные позиции робота. Операторная схема порождает конкретные операторы, которые преобразуют среду. Операторная схема goto(m,n) может быть применена только в том случае, если робот находится в точке m. Поэтому условия ее применимости записываются в виде ATR(m). В результате применения данной операторной схемы робот перейдет из точки m в точку n . Это приведет к изменению состояния среды. Теперь, во множество ППФ, описывающих состояние среды, необходимо добавить утверждение ATR(n) и исключить из него утверждение ATR(m). Следовательно, список добавлений должен содержать предикат AТR(n) , а список вычеркиваний – предикат ATR(m). Таким образом, описание рассматриваемой операторной схемы будет следующим:
Основные модели вывода |
153 |
|
|
goto(m,n); |
ATR(m); |
условия применимости: |
|
список вычеркиваний: |
ATR(m); |
список добавлений: |
ATR(n). |
Необходимо различать параметры операторных схем и обычные квантифицированные переменные, которые также могут входить в операторную схему.
Цель в системе STRIPS также представляется в виде ППФ. Например, если требуется собрать контейнеры k1, k2 и k3 в одной точке, то цель может быть выражена в виде следующей ППФ
G0 x{AT(k1,x), AT(k2,x), AT(k3,x)}. |
(4.1) |
Стратегия поиска решения, используемая в системе STRIPS, основана на методе анализа конечных значений. Метод позволяет осуществлять целенаправленный поиск решений путём анализа различий текущего и целевого состояний среды. Если различие установлено, то выполняется поиск таких операторов, которые могут уменьшить это различие, т.е. приблизить текущее состояние к целевому состоянию. Впервые метод анализа конечных значений был применен в универсальном решателе задач GPS (General Problem Solver) , предназначенном для решения задач интегрального исчисления, логического вывода, игровых задач [18].
Метод анализа конечных значений используется в системе STRIPS совместно с принципом резолюций. Последний позволяет устанавливать выводимость целевых ППФ и выяснять возможность применения операторов к тому или иному состоянию. При выводе целевых ППФ на основе принципа резолюций образуется незавершенное доказательство, которое и выступает в роли различия между текущим и целевым состояниями. Таким образом, в системе STRIPS процесс доказательства теорем ограничен рамками текущего состояния и отделен от процесса поиска в пространстве состояний, который выполняется в соответствии со стратегией, принятой в
GPS.
Представление операторов в системе STRIPS в виде операторных схем привело к необходимости модификации правил унификации. В алгоритме унификации системы STRIPS разрешены следующие виды подстановок:
-вместо переменных могут быть подставлены переменные, константы, параметры и функциональные термы, не содержащие переменных;
-вместо параметров допускается подставлять константы, параметры и функциональные термы, не содержащие функций Сколема, переменных или параметров.

154 |
Глава 4 |
|
|
Кроме этого, потребовалось внести дополнение в процедуру доказательства. Пусть D1 и D2 два дизъюнкта, которые образуют резольвенту D, и={t/p} некоторая подстановка, используемая при получении D, где t – терм, поставляемый вместо параметра p. Дополнение заключаются в том, что р заменяется на t во всех дизъюнктах, являющихся производными от D.
В системе STRIPS поиск решения начинается с попытки доказательства того, что целевая ППФ G0 следует из множества формул М0, определяющих исходное состояние (модель) среды. Для этого система доказывает невыполнимость множества {M0 G0}. Если это доказано, то исходное состояние удовлетворяет цели, и задача решена. Если же невыполнимость множества{M0 G0}не установлена, то образуется незавершенный вывод.
Этот незавершенный вывод рассматривается как различие между M0 и G0 . Далее выполняется поиск операторов-кандидатов, способных уменьшить различие. Для этого выбираются операторы, которые так воздействуют на модель среды, что становится возможным продолжение незавершенного доказательства. Продолжить доказательство позволяют те операторы, в списке добавлений которых имеются литералы, дополнительные к литералам незавершенного доказательства. При этом проверяется, может ли процедура доказательства теорем образовывать резольвенты между дизъюнктами незавершенного доказательства и дизъюнктами из списка добавлений оператора. Если этот факт устанавливается, то оператор с соответствующими значениями параметров, рассматривается как подходящий для уменьшения различия. Когда подходящий оператор найден, то условия его применимости выступают в качестве новой подцели системы.
Подцель в системе STRIPS обрабатывается аналогично цели. Иными словами, система теперь пытается установить невыполнимость множест-
ва{M0 G1}, где G1 – новая подцель, соответствующая условиям применимости выбранного оператора.
Если на данном шаге устанавливается выводимость ППФ G1 из М0, то это означает, что выбранный оператор, например ОР1, может быть применен к состоянию M0. Применив частный вид оператора ОР1, полученного
входе доказательства теоремы М0 G1, система преобразует состояние М0
вновое состояние М1. После этого система вновь попытается установить выводимость G0, но теперь уже из множества формул, описывающих состояние М1. Если же в ходе доказательства теоремы М0 G1 будет полу-
чено незавершенное доказательство, то вновь будет выполняться поиск оператора, обеспечивающего такое изменение М0, чтобы можно было продолжить доказательство. При этом формируется новая подцель, например G2 , а подцели G1 и G0 отодвигаются на второй план. Указанный процесс повторяется, пока не будет доказана цель G0.

Основные модели вывода |
155 |
|
|
Описанный процесс показывает, что, до момента получения окончательного решения, неизвестно какое место в этом решении займет тот или иной оператор. Например, ОР1 может быть применен к исходной модели среды М0 или его применение может быть отложено до момента, когда другой оператор, рассматриваемый после ОР1, преобразует модель к необходимому виду. Такая стратегия сочетает в себе преимущества прямого и обратного поиска. Она дает возможность решить основные подзадачи методом поиска вперед. Затем, чтобы решить вспомогательные подзадачи, возникающие при соединении вместе отдельных частей решения, осуществляется обратный поиск.
Рассмотрим описанные этапы работы системы SRTIPS на примере. Пусть требуется, чтобы робот переместил три контейнера k1,k2 и k3 в одну точку. Исходная модель среды задана множеством формул:
M0 {ATR(a), AT(k1,b), AT(k2,c), AT(k3,d)}.
Целевая формула в этом случае запишется в виде (4.1). Ее отрицание будет иметь вид:
G0 AT(k1,x) AT(k2,x) AT(k3,x) .
Cистеме доступны следующие операторы: goto(m,n) и push(k,m,n). Оператор goto(m,n) описан выше, а оператор push(k,m,n) обеспечивает перемещение объекта k из позиции m в позицию n. Описание данного оператора задается следующим образом:
push(k,m,n);
условия применимости: список вычеркиваний: список добавлений:
AT(k,m) ATR(m); АТ(k,m), ATR(m); AT(k,n), ATR(n).
Решение задачи будем сопровождать построением дерева поиска
(рисунок 4.10).
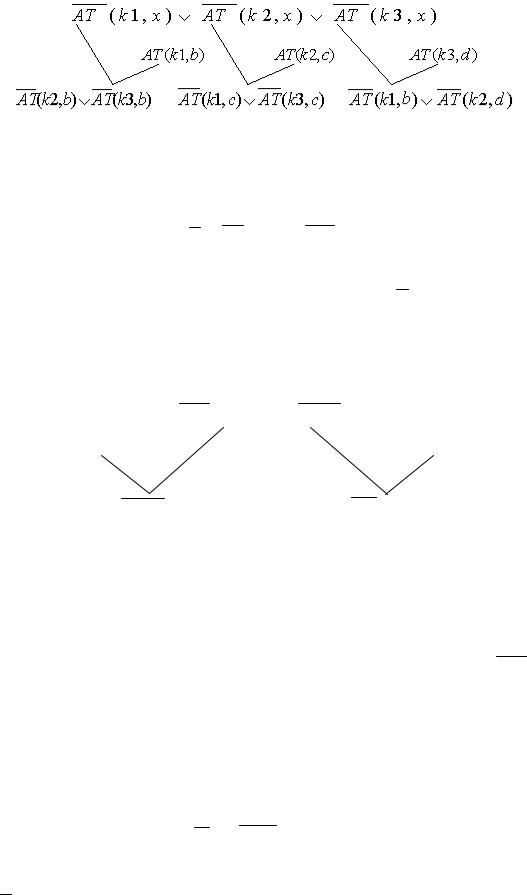
Сначала предпринимается попытка найти противоречие для множества {M0 G0}(вершина (M0,(G0)) на рисунке 4.10). Необходимые построения для данного шага изображены на рисунке 4.11.
Образовавшееся неполное доказательство представляет собой различие текущего и целевого состояний среды. Единственным оператором, способным уменьшить данное различие, является push(k,m,n). В его списке добавлений имеется дизъюнкт АТ(k,n), который позволяет продолжить доказательство. В зависимости от подстановок, выполняемых в параметры k и n, возможны шесть вариантов продолжения доказательства. Каждая из подстановок порождает частный вид оператора. Например, подстановка1 {k2/k,b/n}дает частный оператор OP1: push(k2,m,b).
156 |
Глава 4 |
|
|
(М0,(G0))
(М0,(G1,G0))
(М0,(G2,G1,G0))
OP2: goto(a,c)
(М1,(G1,G0))
OP1: push(k1,c,b)
(М2(G0))
(М2, (G3,G0))
(М2,(G4,G3,G0))
 OP4: goto(b,d)
OP4: goto(b,d)
(М3, (G3,G0))
OP3: push(k3,d,b)
(М4 (G0))
Конечная вершина
М4 =G
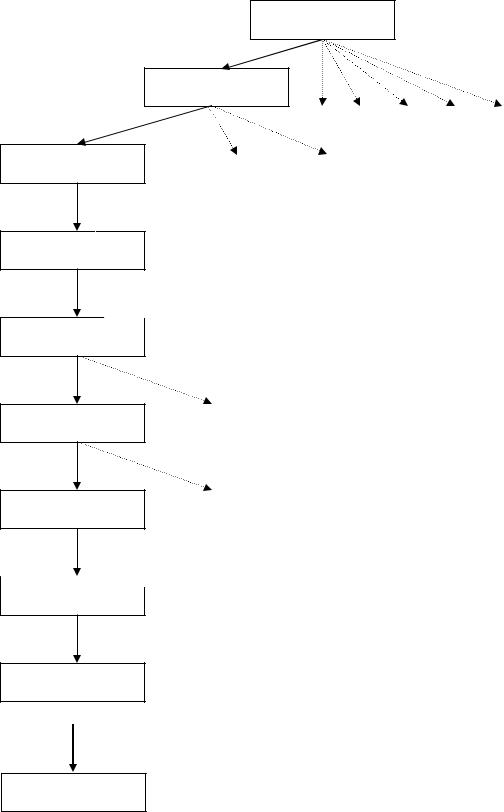
Рисунок 4.10 – Дерево поиска решений в системе STRIPS
Основные модели вывода |
157 |
|
|
Рисунок 4.11 – Неполное доказательство теоремы M0 G0
Оператору ОР1 соответствуют следующее отрицание условий применимости
G1 AT(k2,m) ATR(m) .
Если для продолжения решения будет выбран оператор ОР1, то необходимо доказать невыполнимость множества {M0 G1}(если в дальнейшем окажется, что ОР1 не дает решения задачи, то может быть выбран другой частный вид оператора push). Соответствующее неполное доказательство представлено на рисунке 4.12.
|
AT (k 2, m ) ATR (m ) |
AT(k2,c) |
ATR (a) |
ATR (c) |
AT (k2,a) |
Рисунок 4.12 – Неполное доказательство применимости оператора ОР1
Таким образом, опять образовалось незавершенное доказательство. Одним из подходящих операторов для уменьшения различия будет оператор goto(m,n) , так как в его списке добавлений есть предикат ATR(n), который в случае подстановки 2={c/n} дает резольвенту с предикатом ATR(c). Следовательно, частный вид данного оператора можно записать в форме
OP2: goto(m,c).
Условие применимости данного оператора выступает в качестве новой подцели. Отрицание подцели G2 запишется в виде
G2 ATR(m).
Теперь система пытается установить противоречие для множества {M0 G2}. Данная попытка оказывается успешной, так как в М0 имеется

158 |
Глава 4 |
|
|
литерал ATR(a) , который при подстановке 3={a/m} образует с литералом
ATR(m) контрарную пару. Следовательно, система STRIPS может применить оператор ОР2, имеющий конкретный вид goto(a,c), к состоянию М0. В результате получается новое состояние
M1 {ATR(c),AT(k1,b),AT(k2,c),AT(k3,b)},
и на дереве поиска формируется новая вершина (M1,(G1,G0 )) (рисунок 4.10). Далее система устанавливает, что множество {M1 G1}является противоречием, если выполняется подстановка 4={c/m}. Поэтому она применяет оператор ОР1 с учетом подстановки 4, т. е. push(k2,c,b). В итоге, получается новое состояние:
M2 {ATR(b),AT(k1,b),AT(k2,b),AT(k3,d)}.
На дереве поиска формируется новая вершина (M2,(G0)).
Затем система STRIPS вновь пытается вывести целевую формулу G0, но теперь уже из множества М2. Дальнейшее решение задачи будет протекать так же, как описано выше. Окончательное решение получается в форме:
{goto(a,c), push(k2,c,b), goto(b,d), push(k3,d,b)}.
В заключение отметим, что в системе STRIPS имеется большее число операторов, и она умеет работать с более сложной моделью среды.
4.1.8. Принцип резолюции и язык Пролог
Рассмотренные ранее принципы доказательства теорем нашли свое воплощение в системе (языке) логического программирования Пролог. Собственно говоря, название языка Пролог составлено из двух слов: про- граммирование логическое. В Прологе процесс доказательства теорем рассматривается как процесс вычисления или выполнения программы. Соответствие указанных процессов было установлено Р. Ковальским.
Прежде чем рассмотреть процедуру доказательства теорем, используемую в Прологе, оговорим некоторые элементы синтаксиса языка. Более детальное описание синтаксиса будет приведено позже.
Имена предикатов и констант в Прологе записывают строчными буквами. Имена переменных начинаются с большой буквы или знака подчеркивания. Конкретный список, состоящий из элементов a, b, c, d , записывается на языке Пролог в следующем виде [a,b,c,d]. Список в Прологе может задаваться с помощью переменных, например, [H|T], где Н – голова списка, Т – хвост списка.

Основные модели вывода |
159 |
|
|
Доказательство теорем в Прологе основано на представлении предложений в форме дизъюнктов Хорна. Дизъюнкт Хорна – это предложение, содержащее не более одного положительного литерала. Например,
P Q R S . В Прологе используется три типа дизъюнктов Хорна:
1)дизъюнкт, состоящий только из одного положительного литерала, например, Q;
2)дизъюнкт, содержащий один положительный и произвольное число отрицательных литералов, например, Q P1 P2 ... Pn ;
3)дизъюнкт, состоящий только из отрицательных литералов, напри-
мер, Р1 Р2 ... Рn .
Дизъюнкты первого типа соответствуют фактам пролог–программы, которые представляют истинные утверждения, например, четное_число(2).
Дизъюнктам второго типа соответствуют правила пролог-программы. Правила описывают утверждения, которые могут быть истинными, если выполняются некоторые условия. Отрицательные литералы дизъюнктов Хорна второго типа формируют условие, а положительный литерал – заключение. Например, приведенный выше дизъюнкт Хорна второго типа соответствует импликации (P1 P2 ... Pn) Q , которая на языке Пролог выражается правилом:
q:-p1,p2,…,pn.
В этом правиле импликации соответствует знак “:-”, а конъюнкции соответствует запятая. Положительный дизъюнкт правила в Прологе называют головой правила, а отрицательные дизъюнкты – телом правила.
Дизъюнкт, содержащий только одни отрицательные литералы, т. е. дизъюнкт Хорна третьего типа, соответствует отрицанию целевого утверждения. Использование дизъюнктов Хорна в системе Пролог позволяет применить линейную входную стратегию выбора дизъюнктов, участвующих в решении задачи.
Рассмотрим применение принципа резолюции в системе Пролог на примере. Для этого обратимся к пролог-программе, проверяющей вхождение элемента H в список:
member(H,[H|T]). member(H,[X|T]):-member(H,T).
Здесь member(X,Y) представляет собой предикат, имеющий значение “истина”, если элемент X входит в список Y. Программа состоит из факта member(H,[H|T]) и правила member(H,[X|T]):-member(H,T). С помощью факта задается истинное утверждение о том, что элемент Н и список голов-
