
Точно Не проект 2 / Не books / Источник_1
.pdf50 |
Глава 2 |
|
|
Procedure Hill_Climbing; Begin
n:=‘начальная вершина’; While n<>‘целевая вершина’ Do
Begin
Раскрыть вершину n и для всех дочерних вершин ni вычислить
оценки hˆ(ni);
Выбрать дочернюю вершину ni с минимальным значением hˆ(ni);
If hˆ(ni ) hˆ(n) Then Выход(НЕУДАЧА);
n:=ni;
End;
Выход(УСПЕХ);
End.
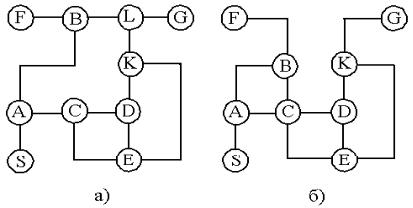
Существуют различные способы построения эвристической оценочной функции, однако готовых рецептов нет. При решении каждой конкретной задачи используют ранее накопленный опыт решения подобных задач. Рассмотрим пример поиска пути в лабиринте (рисунок 2.2). В этом случае
оценка hˆ(ni ) может вычисляться с помощью формулы [86]
hˆ(ni )=|xg - xn| + |yg - yn|,
где xg, yg – координаты целевой вершины; xn, yn – координаты текущей вершины.
Данная оценка соответствует расстоянию от вершины n до целевой вершины. При поиске пути в лабиринте, изображенном на рисунке 2.7,а, последовательность раскрываемых вершин будет следующей: A, B, L, G. Поиск пути в лабиринте, показанном на рисунке 2.7,б, завершится неудачей. При этом последовательность раскрытых вершин будет следующей: А,
В. Оценочная функция в вершине В получит значение 3 Дальнейшие шаги оказываются безуспешными, так как hˆ(F)=3 и hˆ(C)=4, а для продол-
жения поиска необходимо, чтобы выполнялось условие hˆ(ni ) hˆ(n). Таким образом, хотя данный алгоритм обеспечивает ускорение поис-
ка, он не гарантирует достижение целевой вершины. Преждевременное завершение алгоритма происходит в следующих случаях: если в процессе
поиска встречаются локальные минимумы оценочной функции hˆ(n); если для группы соседних вершин оценки hˆ(n) равны между собой (проблема “плато”).
2.2.2.2. Глобальный учет соответствия цели. Этот алгоритм поиска решения задачи похож на предыдущий. Здесь также оценивается “перспективность” того или иного пути с помощью эвристической оценочной функ-
Способы представления задач и поиск решений |
51 |
|
|
ции hˆ(n). Отличие состоит в том, что на каждом этапе выполняется не локальное сравнение вершин, полученных при раскрытии текущей вершины, а глобальное сравнение всех вершин-кандидатов, находящихся в списке OPEN. Для этого список открытых вершин сортируется в порядке возраста-
ния значений hˆ(n). Наилучшая вершина для продолжения пути будет находиться на первом месте в списке OPEN. Поэтому данный алгоритм называют также алгоритмом выбора первой наилучшей вершины (Best-First).
Рисунок 2.7 – Графы состояний
Процедура поиска, основанная на данном алгоритме, похожа на процедуру Optimal_Search. Отличие состоит в том, что вместо функции стоимо-
сти gˆ(n) применяется эвристическая функция hˆ(n), т.е. учитываются только предстоящие затраты:
Procedure Best_First_Search; Begin
Поместить начальную вершину в OPEN; CLOSED:=‘пустой список’;
While OPEN<>‘пустой список’ Do Begin
n:=first(OPEN);
If n=‘целевая вершина’ Then Выход(УСПЕХ);
Переместить вершину n из списка OPEN в список CLOSED; Раскрыть вершину n, для каждой дочерней вершины вычислить hˆ(ni );
Поместить дочерние вершины, которых нет в списках OPEN и CLOSED, в список OPEN, связав с каждой дочерней вершиной ука-
затель на вершину n;
Упорядочить список OPEN по возрастанию значений hˆ(n)
End;
Выход(НЕУДАЧА); End.
52 |
Глава 2 |
|
|
Если данную процедуру применить к задаче поиска пути в лабиринте, изображенном на рисунке 2.7,а, то результат будет таким же, как и в случае алгоритма подъема на гору. Если процедуру Best_First_Search применить к лабиринту, представленному на рисунке 2.7,б, то состояние списка открытых вершин будет следующим:
( S(6) ) ( A(5) ) ( B(3) C(4) ) ( F(3) C(4) ) ( C(4) ) ( D(3) E(4) )( K(2) E(4) ) ( G(0) E(4) ).
Таким образом, алгоритм позволяет успешно справляться с проблемой локальных минимумов. Однако при этом снижается эффективность самого процесса поиска. Эффективность процесса поиска будет оставаться
высокой, если оценка стоимости кратчайшего пути hˆ(n) из вершины n в целевую вершину будет как можно ближе к реальной стоимости h(n)[86].
2.2.2.3. А-алгоритм. Достоинство алгоритма равных цен состоит в том, что он гарантирует нахождение оптимального пути. Достоинством ал-
горитмов, использующих оценку предстоящих затрат hˆ(n), является возможность усечения дерева поиска, что повышает эффективность поиска. Естественным является стремление комбинировать эти алгоритмы и учитывать как сделанные, так и предстоящие затраты. Этого можно добиться, если воспользоваться оценочной функцией
ˆ |
|
ˆ |
ˆ |
(2.1) |
f (n) |
|
g(n) |
h(n), |
где gˆ (n) – оценка стоимости пути из начальной вершины в вершину n; hˆ(n)– оценка стоимости кратчайшего пути из вершины n в целевую вершину.
Алгоритм, базирующийся на использовании оценочной функции fˆ(n), называется А-алгоритмом. Оценки hˆ(n) в ходе поиска не меняют своих значений. Оценки gˆ(n) также не меняют своих значений и всегда равны реальным затратам g(n), если поиск пути выполняется на дереве состояний. Однако при поиске пути на графе состояний оценки gˆ(n) могут меняться.
Следовательно, в общем случае оценки fˆ(n) меняют свои значения в процессе поиска. Это приводит к тому, что вершины из списка CLOSED могут перемещаться обратно в список OPEN:
Procedure A_Search;
Begin
Поместить начальную вершину s в список OPEN: fˆ(s) hˆ(s);
CLOSED:=‘пустой список’;
Способы представления задач и поиск решений |
53 |
|
|
While OPEN<>‘пустой список’ Do Begin
n:=first(OPEN);
If n=‘целевая вершина’ Then Выход(УСПЕХ);
Переместить n из OPEN в CLOSED;
Раскрыть n и для всех ее дочерних вершин ni вычислить оценку
fˆ (n, ni ) gˆ (n, ni ) hˆ(ni ) ;
Поместить дочерние вершины, которых нет в списках OPEN и
CLOSED, в список OPEN, связав с каждой вершиной указатель на вершину n;
Для дочерних вершин ni , которые уже содержатся в OPEN, срав-
нить оценки fˆ(n,ni ) и fˆ(ni ), если fˆ(n,ni )< fˆ(ni ), то связать с вер-
шиной ni новую оценку fˆ(n,ni ) и указатель на вершину n;
Если вершина ni содержится в списке CLOSED и fˆ(n,ni)< fˆ(ni ) , то
связать с вершиной n i новую оценку fˆ(n,ni ), переместить её в список OPEN и установить указатель на n;
Упорядочить список OPEN по возрастанию fˆ(ni );
End;
Выход(НЕУДАЧА); End.
Укажем свойства А-алгоритма. Если для всех вершин hˆ(n)=0, то А- алгоритм будет соответствовать алгоритму равных цен. В этом случае гарантируется нахождения оптимального пути, но эффективность поиска будет низкой, и если пространство поиска будет бесконечно, то поиск просто не осуществим.
А-алгоритм не даёт гарантии, что найденный путь будет оптимальным. Путь может быть не оптимальным в случае, если оценка затрат на пути из вершины n в целевую вершину будет преувеличена (переоценена),
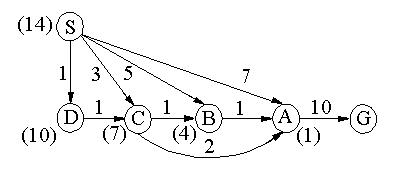
т.е. если hˆ(n)>h(n). Сказанное можно пояснить с помощью рисунка 2.8.
(4)
2 A 5
(6)
S |
|
G |
3 |
(5) |
3 |
|
||
|
B |
|
Рисунок 2.8 – Граф состояний с переоценкой затрат h(n)
54 |
Глава 2 |
|
|
Числа в скобках при вершинах соответствуют оценкам hˆ(n), а рядом с ребрами – стоимости перехода c(ni, nj ). При раскрытии вершины S получаем дочерние вершины А и В. Оценки fˆ(n) для этих вершин, вычисленные с помощью выражения (2.1.), равны: f(A)=2+4, f(B)=3+5. На следующем шаге раскрывается вершина А, и получается f(G)=7+0. Решением будет путь S A G, который для данного графа не является оптимальным.
А-алгоритм обеспечит поиск оптимального пути, если выполняется условие
hˆ(n) h(n). |
(2.2) |
Алгоритм, учитывающий условие (2.2), называют А*- алгоритмом или гарантирующим алгоритмом. А*-алгоритм недооценивает затраты на пути из промежуточной вершины в целевую вершину или оценивает их правильно, но никогда не переоценивает.
Пусть А1* и А2* – произвольные гарантирующие алгоритмы и на всех вершинах hˆ1(n) hˆ2(n). Тогда информированность А1* выше, чем А2*. Говорят, что в этом случае А1* имеет большую эвристическую силу, чем А2*. Эвристически более сильный алгоритм А1* в большей степени сокращает пространство поиска.
Эффективность поиска с помощью А*-алгоритма может снижаться из-за того, что вершина, находящаяся в списке CLOSED, может попадать обратно в список OPEN и затем повторно раскрываться. Следующий пример демонстрирует случай многократного раскрытия вершин (рисунок 2.9).
Рисунок 2.9 – Граф состояний с многократно раскрываемыми вершинами
Состояния списков OPEN и CLOSED показаны в таблице 2.1. Каждая строка таблицы соответствует очередному шагу работы алгоритма. Числа рядом с именами вершин соответствует значениям оценочной функции
fˆ(n). Из таблицы 2.1 следует, что вершина А раскрывается четыре раза, вершина В – 3 раза, вершина С – 2 раза.
Способы представления задач и поиск решений |
55 |
|
|
Таблица 2.1—Выполнение А*-алгоритма
№ |
|
|
OPEN |
|
|
CLOSED |
Комментарий |
1 |
S(14) |
|
– |
|
|
|
|
2 |
A(8) |
B(9) |
C(10) D(11) |
S(14) |
|
|
|
3 |
B(9) |
C(10) D(11) G(17) |
A(8) S(14) |
|
|||
4 |
A(7) |
C(10) D(11) G(17) |
B(9) |
S(14) |
Возврат: А |
||
5 |
C(10) D(11) G(16) |
A(7) B(9) |
S(14) |
|
|||
6 |
A(6) |
B(8) |
D(11) G(16) |
C(10) S(14) |
Возврат: А, В |
||
7 |
B(8) |
D(11) G(15) |
A(6) C(10) S(14) |
|
|||
8 |
D(11) G(15) |
B(8) |
A(6) |
C(10) S(14) |
|
||
9 |
C(9) |
G(15) |
D(11) B(8) A(6) S(14) |
Возврат: С |
|||
10 |
A(5) |
B(7) |
G(15) |
C(9) |
D(11) S(14) |
Возврат: А, В |
|
11 |
B(7) |
G(14) |
A(5) C(9) |
D(11) S(14) |
|
||
12 |
G(14) |
|
B(7) |
A(5) |
C(9) D(11) S(14) |
|
|
Чтобы А*-алгоритм не раскрывал несколько раз одну и ту же вершину, необходимо учитывать условие монотонности
hˆ(ni ) hˆ(n j ) c(ni ,n j ) , |
(2.3) |
где ni – родительская вершина; nj – дочерняя вершина; c(ni, nj ) – стоимость пути между вершинами ni и nj.
Если условие монотонности соблюдается для всех дочерних вершин, то можно доказать, что в тот момент, когда раскрывается некоторая вершина n, оптимальный путь к ней уже найден. Следовательно, оценочная
функция fˆ(n) для данной вершины в дальнейшем не меняет своих значений, и никакие вершины из списка CLOSED в список OPEN не возвращаются.
Ранее отмечалось, что А*-алгоритм недооценивает затраты h(n). Условие монотонности означает, что недооценка на пути к цели становится все меньше или, в крайнем случае, не изменяется. Действительно, если
ˆ |
|
обозначить недооценку через u(n) , то |
|
uˆ(n) h(n) hˆ(n), |
uˆ(n) 0. |
Из условия монотонности следует, что uˆ(nj) uˆ(ni), т.е. недооценка
h(n) в родительских вершинах больше или равна недооценкам h(n) в дочерних вершинах. На графе, изображенном на рисунке 2.9, условие монотонности не выполняется для начальной вершины. Например, h(S)> h(D)+ c(S,D), т.е. 14>10+1.
56 |
Глава 2 |
|
|
Если hˆ(n)=h(n), то информированность является полной. В этом случае никакого поиска не происходит и приближение к цели идет по оптимальному пути.
Таким образом, свойства А-алгоритма существенно зависят от условий, которым удовлетворяет или не удовлетворяет эвристическая часть
оценочной функции fˆ(n):
1)А-алгоритм соответствует алгоритму равных цен, если h(n)=0;
2)А-алгоритм гарантирует оптимальное решение, если hˆ(n) h(n); в этом случае он называется А* – алгоритмом;
3)А-алгоритм обеспечивает однократное раскрытие вершин, если
выполняется условие монотонности hˆ(ni ) hˆ(nj ) c(ni ,nj ) ;
4)алгоритм А1* эвристически более сильный, чем алгоритм А2*
при hˆ1(n) hˆ2(n);
5)А*-алгоритм полностью информирован, если hˆ(n)=h(n);
6)при hˆ(n)>h(n) А-алгоритм не гарантирует получение оптималь-
ного решения, однако часто решение получается быстро. Рассмотренные алгоритмы поиска в пространстве состояний можно
систематизировать с помощью таблицы 2.2.
Таблица 2.2 – Алгоритмы поиска в пространстве состояний
Несисте- |
|
|
|
Систематические |
|
|
|
|
|
||
матичес- |
|
|
|
|
|
|
|
|
|
|
|
кие |
|
|
|
|
|
|
|
|
|
|
|
|
Неинформированные |
|
|
|
Информированные |
|
|
||||
Без оценки затрат |
|
|
С оценками затрат |
|
|
||||||
|
список |
список |
Стои- |
Стоимость до цели |
Стоимость от старта к |
||||||
|
OPEN – |
OPEN– |
мость от |
hˆ(n) |
|
|
цели |
|
|
||
|
механизм |
механизм |
старта |
|
|
fˆ(n) gˆ(n) hˆ(n) |
|||||
|
“LIFO” |
“FIFO” |
gˆ (n) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Случай- |
Поиск в |
Поиск в |
Алго- |
Алгоритм |
|
Глобальный |
|
hˆ(n) h(n) |
|
|
|
ный по- |
глубину |
ширину |
ритм |
подъема |
|
учет соответ- |
|
A*-алгоритм |
|
||
иск |
(Depth) |
(Breadth) |
равных |
на гору |
|
ствия цели |
|
|
|||
|
|
|
hˆ(n) hˆ(n ) c(n,n ) |
||||||||
(Ran- |
|
|
цен |
(Hill |
|
(Best-First) |
|
|
|||
dom) |
|
|
(Optimal |
climbing) |
|
|
|
|
i |
j |
i j |
|
|
|
|
|
|
А* с ограничением |
|||||
|
|
|
search) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
монотонности |
|
||
|
|
|
|
|
|
|
|
|
|
||
Поиск решений в пространстве состояний может выполняться в нескольких направлениях: из начального состояния в целевое состояние (поиск, управляемый данными); из целевого состояния в начальное состояние (поиск, управляемый целью, или обратный поиск); одновременно в двух направлениях (комбинированный поиск). Так как поисковые графы (деревья) для практических задач велики, то двунаправленный поиск может быть
Способы представления задач и поиск решений |
57 |
|
|
эффективнее однонаправленного [35].
Поиск решений в пространстве состояний – комбинаторная задача. Решение получается на основе перебора всех состояний. Однако для многих практических задач полный перебор невозможен. Были предложены различные меры для оценки сложности решаемой задачи. Одна из них – это степень разветвления вершин графа состояния. Она равна среднему числу дочерних вершин, приходящихся на одно состояние задачи. Если рассматривать дерево состояний, то можно вывести формулу, устанавливающую зависимость общего числа состояний N от степени разветвления B и глубины дерева L [77]:
N B(BL 1)/(B 1).
Пусть, например, необходимо подсчитать общее число состояний для игры-головоломки “8”.Укажем возможные перемещения фишек:
-по два перемещения из каждого угла, т.е. для четырех углов восемь перемещений;
-по три перемещения из центральных позиций вдоль каждой из сторон, т.е. всего двенадцать перемещений;
-четыре перемещения из центральной позиции.
Общее число возможных перемещений 24. Разделив это число на 9 (число различных положений для пустой ячейки), получим степень разветвления 2,67. Теперь можно определить общее число состояний при просмотре дерева состояний глубины L (таблица 2.3).
Таблица 2.3 – Число состояний при игре “в восемь”
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
N |
10 |
29 |
80 |
215 |
577 |
1545 |
4127 |
11024 |
29436 |
Как видно из таблицы 2.2, даже для такой простой задачи количество просматриваемых состояний резко возрастает при увеличении глубины поиска.
Сложность решаемой задачи можно также оценивать размерами списков OPEN и CLOSED. Для того чтобы эти списки не разрастались, можно сохранять в списке OPEN только несколько наиболее “перспективных” состояний. Это, конечно, сокращает пространство поиска, но возникает опасность пропуска решения. Такие стратегии поиска, накладывающие ограничения на размер списка OPEN, соответствуют лучевому поиску (beam search). Более безопасны стратегии эвристического поиска, рассмотренные выше. Чем больше информированность о решаемой задаче, тем больший вес имеет эвристическая часть оценочной функции и тем больше сокращается пространство поиска. Следует обратить внимание на то, что вычисление
58 |
Глава 2 |
|
|
эвристик также требует определенных затрат. В этом случае возникает вопрос минимизации общего процессорного времени, затрачиваемого на поиск решения [29].
2.2.3. Поиск с распространением ограничений
Существуют задачи, где необходимо принимать во внимание действующие ограничения на переходы состояний, и благодаря этому целенаправленно идти к её решению. В качестве примера можно привести задачу распознавания речи или задачу интерпретации трехмерных контурных рисунков.
Одна из технологий распознавания речи основана на разбиении речевого сигнала на элементарные участки и присвоении каждому участку метки в виде фонемы. Последовательность фонем, получаемая в результате такой разметки, должна быть согласованной и не противоречить правилам произнесения слов. Ограничения, действующие между возможными взаимными сочетаниями фонем, позволяют исключить из рассмотрения варианты, которые не формируют акустические аналоги слов. Таким образом, элементарные участки речи, представленные фонемами, обеспечивают формирование правильного слова, а последовательность слов – грамматически корректную фразу. В этом смысле накладываемые ограничения позволяют по элементам восстанавливать целое и их часто называют ограни-
чениями целостности.
Если одна и та же переменная участвует одновременно в нескольких ограничениях, то образуются сети (системы) ограничений. Решение задачи в этом случае состоит в определении всех сочетаний значений переменных, которые удовлетворяют ограничениям целостности.
Рассмотрим задачу согласованной разметки (consistent labeling), при решении которой анализируется m элементов, пронумерованных n1,n2,…,nm. Предположим, что каждый элемент ni может быть помечен (интерпретирован) несколькими способами. Количество возможных интерпретаций каждого элемента задается числами b1,b2,…,bm. Если рассматривать возможные интерпретации всей совокупности элементов и проверять их на соблюдение ограничений целостности (т.е. выяснять отображают ли они допустимые решения), то необходимо проанализировать
b1 b2 b3 ... bm случаев. Хотя данная задача легко представляется в виде графа состояний, целесообразнее все же перейти к другому представлению
– к графу, вершины которого есть элементы ni, а ребра соответствуют бинарным отношениям между соответствующими элементами.
Способы представления задач и поиск решений |
59 |
|
|
Пусть для каждого из элементов ni {n1,n2,...,nm} имеется конечное множество интерпретации (меток) Li мощностью Gi. Возможность или невозможность согласованной интерпретации двух элементов ni и nj с помощью меток li L i и l j L j задается бинарным отношением bij. Если
определенная метка li для элемента ni не согласуется с соответствующей меткой lj для элемента nj (т.е. не удовлетворяет отношению bij), то данная метка удаляется из множества Li. Аналогичным образом исследуются все метки, входящие во множество Lj. В ходе указанного процесса с каждой вершиной графа связывается метка (или множество меток). При этом метки на концах ребер графа должны удовлетворять заданным отношениям.
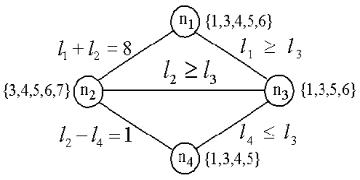
Рассмотрим пример согласованной разметки вершин графа, изображенного на рисунке 2.10 [86]. Около вершин графа указаны множества возможных меток, а ограничения, которым должны удовлетворять соответствующие метки, записаны рядом с ребрами. Основная идея состоит в сужении множества возможных меток для каждой из вершин, опираясь на заданные ограничения.
Рисунок 2.10 – Согласованная разметка узлов графа
Рассмотрим множества совместимых меток для вершин n1 и n2 при ограничении l1+l2=8. Сначала при заданном множестве L1={1,3,4,5,6} удалим из L2 все метки, не удовлетворяющие указанному условию. В данном случае отношение b12 выполняется для всех меток из L2, за исключением метки 6. Следовательно, данная метка удаляется, и L2={3,4,5,7}. Затем отношение b12 используется для проверки множества меток L1. В этом случае из L1 также удаляется метка 6, и множество L1 будет состоять из меток {1,3,4,5}. Таким образом, мы сначала распространили ограничение b12 из вершины n1 в вершину n2, а затем обратно из n2 в n1, удаляя соответствующие метки из множеств L2 и L1. Метки, входящие во множества L2 и L1, теперь согласованы.
На следующем шаге для анализа выбирается вершина, которая связана с наибольшим числом вершин, уже рассмотренных к настоящему моменту. В данном случае это вершина n3. Распространив ограничения от n1 к
