
Точно Не проект 2 / Не books / Источник_1
.pdf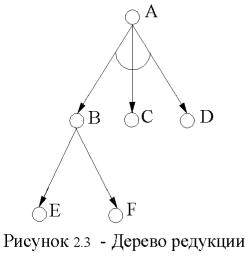
40 |
Глава 2 |
|
|
Граф редукции задачи является графом типа “И-ИЛИ”. С каждой вершиной такого графа можно связать высказывание в виде булевой функции, и поэтому его называют также пропозициональным графом.
На рисунке 2.3 показан частный случай графа редукции задачи – дерево редукции. Здесь А – исходная задача, для решения которой необходимо решить подзадачи В, С и D. Вершина А является конъюнктивной. На рисунке 2.3 это обозначено дужкой, связывающей ветви, ведущие к подзадачам В, С и D. Для решения задачи В необходимо решить одну из ее подзадач E или F. Вершина В является дизъюнктивной.
Граф редукции задачи отличается от графа состояния только тем, что в нем имеются И-вершины. В частном случае, когда на графе редукции отсутствуют И- вершины, И-ИЛИ граф трансформируется в граф пространства состояний. Тогда решение может быть найдено с по-
мощью методов поиска решений в пространстве состояний.
Начальная вершина (корень И-ИЛИ дерева) представляет исходную задачу, которую следует решить. Вершины, соответствующие задачам, решение которых известно, называются заключительными. Задачи и соответствующие вершины, не имеющие решений, называются тупиковыми. Заключительные вершины являются разрешимыми, а тупиковые – неразрешимыми. Разрешимыми являются также И-вершины, у которых разрешимы все дочерние вершины, и ИЛИ-вершины, у которых разрешима хотя бы одна дочерняя вершина. Цель поиска на И-ИЛИ графе – показать, что начальная вершина разрешима. Для этого выполняется построение специального графа, который называется графом решения. Граф решения – это подграф графа редукции задачи с начальной вершиной, соответствующей исходной задаче, содержащий разрешимые вершины. Просмотр графа решения в направлении от заключительных вершин к начальной вершине определяет множество подзадач, которые необходимо решить, и порядок их решения. Рассмотрим примеры представления задач с помощью И-ИЛИ графов.
Решение неопределенных интегралов. Пусть требуется найти не-
определенный интеграл
sin2 xcos4 xdx .
Способы представления задач и поиск решений |
41 |
|
|
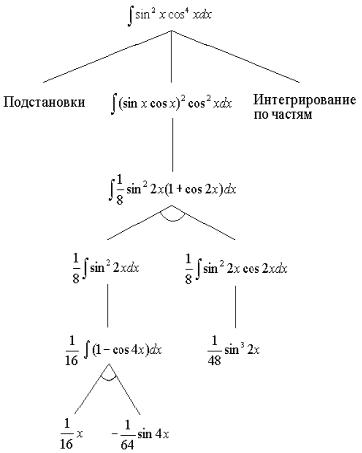
Граф решения данной задачи показан на рисунке 2.4.
Рисунок 2.4 – Вычисление неопределенного интеграла
При нахождении неопределенных интегралов часто используют следующие операторы: всевозможные подстановки (замены), интегрирование по частям, алгебраические преобразования, тригонометрические преобразования и т.п. Исходная задача может быть сведена к множеству подзадач, указанных на рисунке 2.4, с помощью упомянутых выше операторов. Декомпозиция исходной задачи выполняется до тех пор, пока не будут найдены элементарные подзадачи, решение которых известно. Когда такие задачи получены, они помечаются как решенные. Затем выполняется специальная процедура, которая вводит полученные решения во все возможные подзадачи верхних уровней, отмечая, если нужно, каждую подзадачу более высокого уровня как решенную. Если будет отмечена исходная задача, то она считается решенной.
Формирование предложений с помощью формальных грамматик.
Интересно отметить, что конечный И-ИЛИ граф может представлять поро-
ждающую контекстно-свободную грамматику. В этом случае И-вершины соответствуют правилам-продукциям, ИЛИ-вершины – вспомогательным символам, заключительные вершины – терминальным символам (см. §8.6).
42 |
Глава 2 |
|
|
Рассмотрим процесс генерации синтаксически правильных предложений английского языка как пример задачи, которая сводится к решению подзадач. Задача состоит в том, чтобы формировать предложения в соответствии с грамматикой, заданной совокупностью правил-продукций:
1) S |
SUB PRED; |
|
2) SUB |
PRON; |
|
3) SUB |
NP; |
|
4) PRED |
V NP; |
|
5) NP |
DET N; |
|
6) |
PRON |
he; |
7) |
PRON |
it; |
8) |
DET |
a; |
9) |
DET |
the; |
10) V |
saw; |
|
11) V |
carried; |
|
12) N |
dog; |
|
13) N |
man. |
|
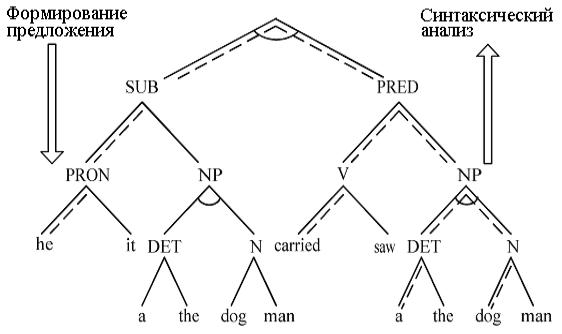
Здесь строчными буквами обозначены терминальные элементы, а прописными буквами – нетерминальные. Символ S обозначает начальный символ. Начиная с S, нужно построить последовательность из терминальных символов, представляющую синтаксически правильные предложения. Применяя к S правило 1, сведем задачу формирования предложения S к задаче формирования символов SUB и PRED. Теперь задача состоит в том, чтобы преобразовать каждый из символов SUB и PRED в последовательность терминальных символов. Эти подзадачи проще исходной. Они также могут быть сведены к более простым подзадачам путем применения правил 2, 3 и 4. Продолжая указанный процесс, получим дерево редукции задачи, изображенное на рисунке 2.5 .
Штриховыми линиями на рисунке показано возможное дерево решения, в соответствии с которым формируется последовательность из терминальных элементов, образующая английское предложение “he carried a dog” (он нес собаку). С помощью рассматриваемой грамматики можно сформировать 48 правильных предложений: “the man saw a dog”, “the dog carried the man” и т.п. Безусловно, данные предложения корректны только в отношении синтаксиса. Семантика предложения здесь не рассматривается. Таким образом, дерево решения, представленное на рисунке 2.5, соответствует дереву вывода некоторого высказывания в контекстно-свободной грамматике. Поиск деревьев решений может выполняться с привлечением методов теории формальных грамматик.
В дереве, изображенном на рисунке 2.5, имеются повторяющиеся вершины, например NP. Такие вершины соответствуют одним и тем же подзадачам. Если совместить две вершины NP, то дерево редукции транс-
Способы представления задач и поиск решений |
43 |
|
|
формируется в граф редукции. Методы поиска решений в пространстве редукции задачи должны исключать повторное рассмотрение уже решенных подзадач.
Рисунок 2.5 – Граф редукции задачи формирования предложений
Игры для двух игроков-противников. Имеется большой класс игр с нулевой суммой и полной информацией для двух лиц, например: шахматы, шашки, игра “го” и др. В этих играх игрок обладает полной информацией о текущей игровой ситуации. Причем, если один игрок что-либо выигрывает, то другой столько же проигрывает. Возможны два исхода игры: выигрыш и проигрыш.
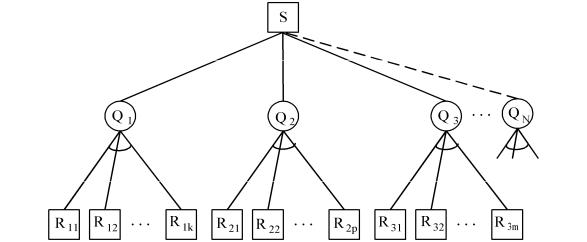
Представим игру в виде И-ИЛИ графа. Так как ходы игроков выполняются по очереди, то на графе выделяют два вида позиций – МАКС и МИН (рисунок 2.6). На рисунке позиции, соответствующие игроку МАКС обозначены квадратом, а игроку МИН – кругом. Игрок, в пользу которого решается игра, обычно называется МАКС. Пусть в начальной позиции S игрок МАКС может сделать любой ход. Каждый ход игрока МАКС приводит к одной из возможных позиций Q1,Q2,…,QN игрока МИН, а ответный ход МИН (противника) в позиции Q1 приводит к новым возможным позициям игрока МАКС (т.е. R11,R12,…,R1k).
Для того чтобы игрок МАКС выиграл в позиции S, необходимо найти такой ход из позиции S, который создает выигрышную позицию Qi. Таким образом, МАКС выигрывает в позиции S, если он выигрывает или в позиции Q1, или Q2, или Q3 и т.д. Следовательно, S – это ИЛИ вершина. Так как МАКС выигрывает в позиции Qi,, то он должен выигрывать после
44 |
Глава 2 |
|
|
любого ответного хода противника, т.е. и в позиции Ri1, и в Ri2, и в Ri3 и т.д. Таким образом, все позиции, в которых выбор должен сделать игрок МИН, – это И-вершины.
Рисунок 2.6 – И-ИЛИ дерево игры для двух игроков
Чтобы решить задачу, необходимо построить дерево игры, обеспечивающее победу игрока МАКС независимо от ответных ходов игрока МИН. Поскольку поиск дерева игры имеет свои особенности, ниже посвятим этому отдельный параграф.
2.1.3. Представление задач в виде теорем
При представлении задач в форме доказательства теорем возможные состояния задачи, включая начальные и целевые состояния, рассматриваются как правильно построенные формулы исчисления предикатов, которое будет рассмотрено позже. Операторы, отображающие одно состояние в другое, рассматриваются как правила, которые выводят одно правильно построенное выражение из другого. Процесс решения задачи в этом случае протекает следующим образом:
a) формируется множество исходных истинных утверждений (аксиом) относительно условия задачи, записываемых в виде формул языка исчисления предикатов; б) строится гипотеза относительно результата решения задачи, кото-
рая то же записывается на языке исчисления предикатов и называется целевым утверждением; в) аксиомы комбинируются между собой на основе допустимых пра-
вил вывода с целью получения множества новых утверждений; г) проверяется, не содержит ли множество новых утверждений целе-
вое утверждение или его отрицание; если содержит, то теорема считается доказанной, и процесс решения задачи на этом заканчивается;
Способы представления задач и поиск решений |
45 |
|
|
если целевое утверждение или его отрицание не входят в множество вновь сформированных утверждений, то полученное множество утверждений объединяется с множеством исходных аксиом и процесс повторяется.
Рассмотренный процесс поиска решений представляет собой логическую формализацию хода решения задачи в пространстве состояний методами полного перебора. Такой метод гарантирует нахождение решения, если оно существует. Однако непосредственное его применение ограничено, так как полный перебор может потребовать больших ресурсов времени и памяти.
Для управления поиском используют различные стратегии выбора пар аксиом или промежуточных утверждений, участвующих в выводе, что позволяет внести систематичность в процесс поиска и сократить число возможных комбинаций различных утверждений в процессе вывода.
Основные процедуры логического вывода рассматриваются в главе 4 после изложения основ исчисления предикатов.
2.2. Поиск решений задач в пространстве состояний
Методы поиска в пространстве состояний подразделяются на две группы: методы “слепого” и упорядоченного (эвристического) поиска. Достоинством методов “слепого” поиска является простота алгоритмической реализации и гарантированность получения решения, если оно существует. Методы “слепого” поиска называют также “неинформированными” методами, так как в процессе поиска пути на графе не учитывается информация о степени близости текущей и целевой вершин. Это приводит к тому, что в методах “слепого” поиска выполняется полный просмотр всего пространства состояний. Для нетривиальных задач такой просмотр невозможен из-за слишком большого размера пространства состояний. В этом случае возникает проблема комбинаторного взрыва, когда размер пространства решений возрастает чрезвычайно быстро с ростом числа рассматриваемых альтернатив. Эффективным средством борьбы с комбинаторной сложностью являются методы эвристического поиска, позволяющие существенно снизить объем поиска в больших пространствах решений.
В рассматриваемых ниже алгоритмах поиска используются два списка: список открытых вершин и список закрытых вершин. В списке открытых вершин (OPEN) находятся идентификаторы (имена) вершин, подлежащих раскрытию; в списке закрытых вершин (CLOSED) находятся имена вершин, раскрытых к данному моменту, и имя вершины, раскрываемой на текущем шаге работы алгоритма.
46 |
Глава 2 |
|
|
2.2.1.Методы “слепого” поиска
2.2.1.1.Случайный поиск. Случайный поиск реализуется простым алгоритмом. Информированность при случайном поиске ограничивается топологией графа пространства состояний. Стратегия поиска состоит в том, что, начиная с начального состояния, случайно выбирают оператор, осуществляющий переход к следующему состоянию задачи. Поиск продолжается до тех пор, пока не будет выполнен переход в целевое состояние.
Ниже приведена процедура случайного поиска на псевдоязыке:
Procedure Random_Search; Begin
n:=‘начальная вершина’;
While n <>‘целевая вершина’ Do
Begin
Выбрать случайно оператор, применимый к ‘n’;
Применить данный оператор к ‘n’ и получить новую вершину
‘n_New’; n:=n_New;
End.
Случайный выбор оператора не гарантирует сходимость алгоритма. Тем не менее, такой метод поиска обеспечивает решение простых задач, с ограниченным пространством поиска, при наличии пути между начальной и целевой вершиной.
Так как граф состояний обследуется случайным образом, без запоминания пройденного маршрута, возможен многократный выбор одних и тех же состояний. Улучшить процедуру поиска можно введением определенной систематичности выбора переходов состояния.
2.2.1.2. Поиск “в глубину и ширину”. Данные методы исключают бесполезный повторный выбор одних и тех же вершин. Для этого с помощью списков CLOSED и OPEN ведется соответственно учет уже раскрытых вершин и вершин, подлежащих раскрытию. Кроме этого, задается определенный порядок (систематичность) обследования графа состояния, что позволяет последовательно пройти все маршруты по одному разу, без пропусков и повторений. Рассмотрим процедуру поиска в глубину:
Procedure Depth_First;
Begin
Поместить начальную вершину в список OPEN;
CLOSED:=‘пустой список’;
While OPEN<>‘пустой список’ Do
Begin
Способы представления задач и поиск решений |
47 |
|
|
n:=first(OPEN);
If n=‘целевая вершина’ Then Выход(УСПЕХ); Переместить n из списка OPEN в CLOSED;
Раскрыть вершину n и поместить все ее дочерние вершины, отсут-
ствующие в списках OPEN и CLOSED, в начало списка OPEN, свя-
зав с каждой дочерней вершиной указатель на n;
End;
Выход(НЕУДАЧА);
End.
В начале поиска список CLOSED пустой, а OPEN содержит только начальную вершину. Каждый раз из списка OPEN выбирается для раскрытия первая вершина (вызов функции first(OPEN)). Раскрытая вершина перемещается в список CLOSED, а ее дочерние вершины помещаются в начало списка OPEN. Таким образом, на следующем шаге будут раскрываться дочерние вершины текущей вершины n. Принцип формирования списка OPEN в этом случае соответствует стеку, т.е. вершина, добавленная в список последней, обрабатывается первой (LIFO – Last In First Out). Если проследить направление поиска по дереву состояний, то фронт поиска растет в глубину. Для построения обратного пути (из целевой вершины в начальную вершину) все дочерние вершины снабжаются указателями на соответствующие родительские вершины.
Процедура поиска в ширину отличается от рассмотренной процедуры поиска в глубину тем, что дочерние вершины, получаемые при раскрытии вершины n, помещаются в конец списка OPEN. Следовательно, при поиске в ширину принцип формирования списка OPEN соответствует очереди, т.е. вершина, внесенная в список первой, обрабатывается первой (FIFO – First In First Out). Благодаря этому фронт поиска растет в ширину, что гарантирует нахождение пути с минимальным количеством дуг (ребер) между исходной и целевой вершинами (своего рода оптимальность).
2.2.1.3. Алгоритм равных цен. Информированность о решаемой задаче здесь выше, чем в случае поиска в глубину и ширину. Каждому оператору, преобразующему состояние ni в состояние nj, ставится в соответствие некоторая функция стоимости c(ni,nj ), характеризуемая положительными значениями. В ходе поиска пути на графе учитываются суммарные затраты для достижения той или иной вершины, т.е. стоимость пути к этой вершине. Стоимость пути к вершине nj может быть определена по следующей формуле
g(nj)=g(ni )+c(ni, nj ),
где g(ni ) – стоимость пути из начальной вершины в вершину ni .
В ходе поиска вершины в списке OPEN сортируются в порядке увеличения стоимости. Каждый раз раскрывается вершина с наименьшей стои-
48 |
Глава 2 |
|
|
мостью. Это позволяет найти путь минимальной стоимости из начальной вершины в целевую вершину. Следует отметить, что в процессе поиска стоимость пути к вершине может меняться, если обнаруживается более дешевый путь. Поэтому будем обозначать стоимость оптимального пути из начальной вершины в вершину n через g(n), а стоимость текущего пути, найденного алгоритмом, через gˆ(n), т.е. gˆ(n) – это оценка стоимости пути g(n). В конце поиска gˆ(n) = g(n).
Ниже представлена процедура поиска оптимального пути (минимальной стоимости), записанная на псевдоязыке:
Procedure Optimal_Search;
Begin
Поместить начальную вершину в список OPEN;
CLOSED:=‘пустой список’;
While OPEN<>‘пустой список’ Do n:=first(OPEN);
If n=‘целевая вершина’ Then Выход(УСПЕХ); Переместить вершину n из списка OPEN в CLOSED;
Раскрыть вершину n, для каждой дочерней вершины i вычислить стоимость gˆ(n,ni );
Поместить дочерние вершины, которых нет в списках OPEN и CLOSED, в список OPEN, связав с каждой вершиной указатель на
вершину n и положить gˆ(ni)= gˆ(n,ni );
Для каждой из дочерних вершин, которые уже содержатся в списке
OPEN, сравнить текущую стоимость gˆ (n, ni ) с ранее вычислен-
ным значением стоимости gˆ(ni ), хранящемся в списке OPEN, если gˆ(n,ni)<gˆ(ni), то установить gˆ(ni )=gˆ(n,ni ). Снабдить указанные
дочерние вершины указателями на вершину n;
Упорядочить список OPEN по возрастанию стоимости; End;
Выход(НЕУДАЧА); End.
В тот момент, когда раскрывается некоторая вершина n, оптимальный путь к этой вершине уже найден, т.е. gˆ(n)=g(n) [86]. Иными словами, если вершина уже находится в начале списка OPEN, то для нее невозможно найти более дешевого пути. Следовательно, перевод вершины в список CLOSED является окончательным.
Рассмотренная процедура поиска гарантирует нахождение пути минимальной стоимости, если граф конечен и существует путь из начальной вершины в целевую вершину. Однако сам процесс поиска не является оптимальным, так как поиск выполняется без учета положения целевых вершин.
Способы представления задач и поиск решений |
49 |
|
|
2.2.2. Эвристический поиск
Основная идея эвристического поиска состоит в использовании дополнительной информации для управления процессом поиска. Эта дополнительная информация формируется на основе эмпирического опыта, догадок и интуиции исследователя, т.е. эвристик. Использование эвристик позволяет сократить количество просматриваемых вариантов при поиске решения задачи, что ведет к более быстрому достижению цели.
В алгоритмах эвристического поиска список открытых вершин упорядочивается по возрастанию некоторой оценочной функции, формируемой на основе эвристических правил. Оценочная функция может включать две составляющие, одна из которых называется эвристической и характеризует близость текущей и целевой вершин. Чем меньше значение эвристической составляющей оценочной функции, тем ближе рассматриваемая вершина к целевой вершине. В зависимости от способа формирования оценочной функции выделяют следующие алгоритмы эвристического поиска: алгоритм “подъема на гору”, алгоритм глобального учета соответствия цели, А-алгоритм.
2.2.2.1. Алгоритм “подъема на гору”. Алгоритм осуществляется целенаправленный поиск в направлении наибольшего убывания эвристиче-
ской оценочной функции hˆ(n). Данная функция обеспечивает оценку (прогноз) стоимости кратчайшего пути от текущей вершины n до ближайшей целевой вершины, т.е. является мерой стоимости оставшегося пути. Чем меньше значение hˆ(n), тем более “перспективен” путь, на котором находится вершина n.
Подобный алгоритм используется при поиске экстремумов функции. Известно, что положение экстремума функции многих переменных определяется направлением вектора градиента функции. Поэтому поиск экстремума осуществляют в направлении наибольшего возрастания (убывания) функции, т.е. в направлении, совпадающем (или противоположном) с направлением градиента. Поиск максимума функции в этом случае напоминает восхождение на пик по наиболее крутому маршруту. Поэтому рассматриваемый алгоритм и называют алгоритмом “подъема на гору” (hill – climbing).
На очередном шаге алгоритма для каждой из дочерних n2,...,nm вершины n вычисляется значение оценочной функции продолжения пути выбирается вершина с наименьшим значением
Процедура поиска терпит неудачу, если для всех дочерних вершин hˆ(ni ) hˆ(n):
