
Точно Не проект 2 / Не books / Источник_1
.pdf170 |
Глава 4 |
|
|
Кроме этого, при введении новой гипотезы, необходимо заново пересчитывать таблицы вероятностей, что также ограничивает применимость байесовского подхода. Тем не менее, он достаточно широко применяется в экспертных системах, благодаря хорошему теоретическому фундаменту. Важно, что после многократного применения теоремы Байеса влияние всех исходных допущений на результат становится минимальным. Поэтому, хотя априорные вероятности могут определяться приближенно, их соотношение вычисляется достаточно надежно. Свое дальнейшее развитие рассматриваемый подход получил в байесовских сетях доверия [77].
4.2.2.2. Метод коэффициентов уверенности. Метод коэффициентов уверенности был впервые применен в экспертной системе MYCIN. В отличие от байесовского подхода, который использует теорию вероятностей для подтверждения гипотез, метод системы MYCIN базируется на эвристических соображениях, которые были позаимствованы из практического опыта работы экспертов. Когда эксперт оценивает степень достоверности некоторого вывода, он использует такие понятия, как “точно”, “весьма вероятно”, “возможно”, “ничего нельзя сказать” и т.п. Разработчики системы MYCIN решили отобразить эти размытые понятия на шкалу коэффициентов уверенности, изменяющихся в диапазоне от –1 до +1. Для этого были введены две оценки – MB и MD. Оценка MB отражает степень истинности некоторого факта (свидетельства) и принимает значения от 0 до +1. Оценка MD соответствует степени ложности некоторого факта и принимает значения в диапазоне от –1 до 0. Коэффициент уверенности факта, обозначаемый CF, определяется как разность оценок MB и MD:
CF MB MD .
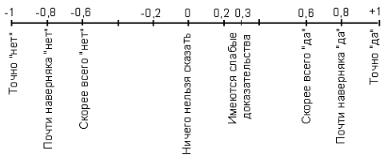
Здесь 0<MB<1 (при MD=0) и –1<MD<0 (при MB=0). Если коэффициент уверенности принимает значение, равное +1, то факт считается истинным. Если CF= -1, то факт ложный. Шкала изменения значений коэффициентов уверенности изображена на рисунке 4.16 [53].
В ходе логического вывода над фактами, составляющими предпосылки правил, выполняются логические операции. В результате этого образуются сложные высказывания, коэффициенты уверенности которых вычисляются по следующим правилам:
1) при логической связи И между фактами P1 и P2
CF(P1 P2 ) MIN(CF(P1),CF(P2 ));
2) при логической связи ИЛИ между фактами P1 и P2
CF(P1 P2) MAX(CF(P1),CF(P2 )).
Основные модели вывода |
171 |
|
|
Рисунок 4.16 – Шкала коэффициентов уверенности
В системе MYCIN коэффициенты уверенности приписываются не только фактам, но и правилам. Таким способом обеспечивается учет ненадежности правил, которые часто формируются на основе эвристических соображений. Обозначим коэффициент уверенности правила через CFR. Коэффициент CFR соответствует степени истинности заключения правила при истинных предпосылках. Если предпосылки характеризуются коэффициентом уверенности CFпред 1, то коэффициент уверенности заключения CFзакл вычисляют по формуле
CFзакл CFпред CFR .
Рассмотрим пример правила (P1 P2 ) P3 C1(0,9), где P1,P2,P3 – факты, образующие предпосылки правила; C1 – заключение правила; 0,9 – коэффициент уверенности правила. Пусть факты характеризуются следующими коэффициентами уверенности: CF(P1)=0,8; CF(P2)=0,6; CF(P3)=0,7. Определим коэффициент уверенности заключения CF(C1):
CF(P1 P2 ) min(0,8;0,6) 0,6;
CF((P1 P2 ) P3) max(0,6;0,7) 0,7;
CF(C1) 0,7 0,9 0,62.
В процессе логического вывода одно и то же заключение может подтверждаться различными правилами, каждое из которых приписывает заключению свой коэффициент уверенности. Очевидно, что коэффициент уверенности заключения, подтверждаемого несколькими правилами должен увеличиться. Чем больше будет иметься подтверждений в пользу некоторого заключения, тем ближе к единице должен быть его коэффициент уверенности. В общем случае комбинация свидетельств в поддержку некоторого заключения выполняется по следующим формулам, используемым в системе EMYCIN [37,54]:

172 |
Глава 4 |
|
|
CF CF1 |
CF2 |
CF1 |
CF2,если |
CF1 |
0,CF2 |
0; |
|
||
CF CF1 |
CF2 |
CF1 |
CF2,если |
CF1 |
0,CF2 |
0; |
|
||
CF |
|
CF1 CF2 |
|
,если |
CF |
CF 0,CF 1,CF 1; |
|||
|
|
|
|||||||
1 min(|CF1 |,|CF2 |) |
|
1 |
2 |
1 |
2 |
||||
|
|
|
|
|
|||||
Если |
CF1 1 |
и |
CF2 |
1, |
то |
CF 1. |
|
||
Коэффициенты уверенности заключений, формируемых тремя или более правилами, можно вывести последовательно, применяя указанные выше формулы.
В заключение отметим, что метод коэффициентов уверенности благодаря своей простоте находит широкое применение во многих системах, поддерживающих вывод на ненадежных знаниях. Недостатки метода связаны с отсутствием теоретического фундамента, а также сложностью подбора значений коэффициентов уверенности.
4.2.2.3.Теория свидетельств Демпстера-Шефера. Подход, принятый
втеории Демпстера-Шефера (ТДШ), отличается от байесовского подхода и метода коэффициентов уверенности тем, что, во-первых, здесь используется не точечная оценка уверенности (вероятность, коэффициент уверенно-
сти), а интервальная оценка. Такая оценка характеризуется нижней и верхней границей, что более надежно. Во-вторых, ТДШ позволяет исключить взаимосвязь между неопределенностью (неполнотой знаний) и недоверием, которая свойственна байесовскому подходу.
В рамках ТДШ множеству высказываний А приписывается диапазон значений [ Bl(A),Pl(A)], в котором находятся степени доверия каждого из высказываний. Здесь Bl(A) – степень доверия к множеству высказываний, изменяющая свои значения от 0 (нет свидетельств в пользу А) до 1 (множество высказываний А истинно); Pl(A) – степень правдоподобия множества высказываний А, определяемая с помощью формулы
Pl(A) 1 Bl(A).
Значения степени правдоподобия также лежат в диапазоне от 0 до 1. Степень правдоподобия множества высказываний А – это величина обратная
степени доверия к множеству противоположных высказываний А. Если
имеются четкие свидетельства в пользу А, то Bl( А)=1, и степень правдоподобия А равна нулю, т.е. Pl(A)=0. При Pl(A)=0 степень доверия Bl(A) тоже равна нулю.
В случае отсутствия информации в поддержку той или иной гипотезы полагается, что диапазон изменения значений степеней Bl и Pl равен [0, 1]. По мере получения свидетельств указанный диапазон сужается. В теории
Основные модели вывода |
173 |
|
|
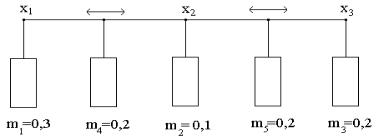
Демпстера-Шефера неопределенность знаний представляется с помощью некоторого множества Х. Элементы этого множества соответствуют возможным фактам или заключениям. Неопределенность состоит в том, что заранее неизвестно, какое из возможных значений примет факт или заключение х Х . Для характеристики степени определенности в ТДШ вводится некоторая единичная мера уверенности (ее называют также единичной массой уверенности), которая распределяется между элементами Х. При этом, если вся масса (степень) уверенности приходится на один элемент х Х , то никакой неопределенности нет. Неопределенность возникает, когда масса уверенности распределяется между несколькими элементами х Х . На рисунке 4.17 изображено распределение масс уверенности между элементами множества Х, представленного в виде точек. Здесь
Х={x1, x2, x3}.
Рисунок 4.17 – Распределение масс уверенности
С каждым элементом множества Х жестко связана соответствующая масса уверенности. Так, х1 соответствует m1=0,3 , x2 – m2=0,1, x3 – m3=0,2. Имеются также свободные массы уверенности m4=0,2 и m5=0,2, которые относятся сразу к нескольким элементам. Масса m4 свободно перемещается между элементами х1 и x2 , а масса m5 – между элементами x2 и x3, т.е. m4 закреплена за подмножеством {х1, x2}, а m5 – за подмножеством {x2, x3}. Массы выражают степень уверенности в возможных значениях фактов или заключений. Так, степень уверенности в значении х1 может изменяться от 0,3 до 0,5. Таким образом, степень незнания соответствует массе, местоположение которой не определено.
В общем случае распределение масс уверенности задается функцией m(A), обладающей следующими свойствами:
m( ) 0,
m(A) 1.
A X
Здесь А – множество, образованное из подмножеств Х, которым назначены соответствующие массы (степени) уверенности; m(A) – функция,

174 |
Глава 4 |
|
|
которая задает отображение А на интервал [0, 1]. Для примера, изображенного на рисунке 4.17
А{ ,{x1},{x2},{x3},{x1,x2},{x2,x3},{x1,x3}},
араспределение масс уверенности задаётся функцией m(A), характеризуемой множеством значений
m(A) {0;0,3;0,1;0,2;0,2;0,2;0}.
Обратим внимание, что А состоит из подмножеств. Обозначим каждое такое подмножество через Аi. Степень доверия к высказываниям, соответствующим подмножеству Ai, может быть вычислена по формуле
Bl(Ai ) m(Aj ). |
(4.8) |
Aj Ai
Здесь суммирование выполняется по всем подмножествам Aj, входящим в Ai. Например,
Bl({x1,x2}) m(A1) m(A2) m(A4 ) m({x1}) m({x2}) m({x1,x2})
0,3 0,1 0,2 0,6.
Соответствующие значения степеней доверия для всех остальных подмножеств Ai представлены в таблице 4.1
Таблица 4.1 – Значения Bl(Ai) и Pl(Ai)
|
|
{ |
{x2} |
|
|
{ |
|
{ |
{ |
{ |
X |
i |
|
x1} |
|
|
x3} |
|
x1,x2} |
|
x2,x3} |
x1,x3} |
|
B |
0 |
0 |
|
0 |
0,2 |
|
|
0 |
0 |
0 |
1 |
l(Ai) |
|
,3 |
,1 |
|
|
|
,6 |
|
,5 |
,5 |
|
P |
0 |
0 |
|
0 |
|
0 |
|
0 |
0 |
0 |
1 |
l(Ai) |
|
,5 |
,5 |
|
,4 |
|
,8 |
|
,7 |
,9 |
|
Степень правдоподобия подмножества Ai определяется по формуле
Pl(Ai ) 1 Bl(Ai ) 1 m(Aj ). |
(4.9) |
||
Aj |
Ai |
|
|
Результаты вычислений степеней правдоподобия приведены в таблице 4.1. Величины Bl(Ai) и Pl(Ai) имеют простую интерпретацию: Bl(Ai) представляет общую массу уверенности, которая остается, если из Х удалить все элементы, не ассоциируемые с Ai ; Pl(Ai) представляет максимальную массу уверенности, которую можно получить, если сдвинуть свободные массы к элементам множества Ai. Причем Bl(Ai ) Pl(Ai ). Иными словами,
Bl(Ai) представляет нижнюю границу доверия к Ai, а Pl(Ai) – верхнюю.

Основные модели вывода |
175 |
|
|
Важнейшим элементом ТДШ является правило комбинации свидетельств:
|
|
m1(A1i ) m2 (A2 j ) |
|
||
m(A ) |
A1i A2 j |
|
|
||
1 |
m1(A1i ) m2 (A2 j ) . |
(4.10) |
|||
k |
|||||
A1i A2 j
Сумма в числителе правила распространяется на множество
Ak A1i A2 j . Правило является эвристическим и позволяет осуществлять распределение степеней доверия в ходе вывода [37].
4.2.2.4. Нечеткие множества и нечеткая логика. Для формализации нечетких знаний, характеризуемых лингвистической неопределенностью, применяется теория нечетких или расплывчатых множеств. Основы теории нечетких множеств были созданы в 1965г. американским математиком Л.А.Заде. Пусть имеется множество Х и его собственное подмножество А, т.е. A X. Тогда подмножество A можно представить в виде совокупности упорядоченных пар
A {(x, A (x))}, x X,
где A (x) – функция принадлежности. Причем
1,если |
x A, |
|
A(x) |
если |
x A. |
0, |
||
Рассмотрим в качестве примера множество, представляющее возможные значения температуры воздуха. Тогда введение функции принадлежности, условно изображенной на рисунке 4.18 сплошной линией, позволит выделить подмножество отрицательных температур, а изображенной пунктирной линией – подмножество положительных температур. При этом нулевая температура относится ко второму подмножеству.
Рисунок 4.18 – Функция принадлежности для четкого множества

176 |
Глава 4 |
|
|
Приведенное определение подмножества A и пример функции принадлежности, принимающей всего два возможных значения 0 и 1, соответствует четкому (обычному) подмножеству. Определение нечеткого подмножества получается как обобщение этого определения. Нечетким подмножеством А множества Х будем называть совокупность упорядоченных пар
A {(x, A(x))}, x X , |
(4.11) |
где функция принадлежности A (x) каждому элементу х ставит в соответствие действительное число из интервала [0,1], указывающие степень принадлежности элемента х подмножеству А. Часто в выражении (4.11) вме-
сто запятой, отделяющей х от A (x), используется вертикальная черта, т.е.
пишут (x| A(x)). Это позволяет исключить возможную путаницу, когда значения функции принадлежности задаются числами, в которых дробная часть отделяется от целой запятой.
Математическая структура, определяемая выражением
A {(x1 |0,8),(x2 |0,3),(x3 |0),(x4 |0,5)},
где х1,х2,х3,х4 – элементы универсального множества Х, представляет собой пример нечеткого подмножества. Здесь степени принадлежности элементов х1, х2 , х3, х4 подмножеству А заданы числами после вертикальной черты. Наивысшую степень принадлежности имеет элемент х1. Элемент х3 подмножеству А не принадлежит1). Элементы х2 и х4 принадлежат А в меньшей степени, чем х1 . Таким образом, используя понятие нечеткого подмножества, можно представлять объекты (сущности) предметной области, характеризуемые размытыми границами описаний.
Нечеткое подмножество A называется нормальным, если
max A (x) 1.
x X
Если это свойство не выполняется, то А называется субнормальным. Непустое подмножество А всегда можно нормализовать делением на максимальное значение функции принадлежности. Носителем нечеткого подмножества А называется подмножество элементов Х, для которыхA (x) 0 . Переменная х в выражении (4.11) называется базовой. В дальнейшем, говоря о нечетких подмножествах, будем опускать приставку
“под”.
При практическом применении нечетких множеств важными являются понятия нечеткой и лингвистической переменной. Нечеткая переменная
1) Обычно элементы с принадлежностью 0 не записываются
Основные модели вывода |
177 |
|
|
определяется набором , X,R , где |
– название нечеткой перемен- |
ной; Х={x} – область ее определения; R – нечеткое подмножество множества Х, включающее те возможные значения х, которые обусловлены названием . Лингвистической называют переменную, значениями которой являются слова и фразы естественного языка (термы). Формально лингвистическая переменная определяется набором [31]
,T, X,G,M ,
где – название переменной; Т – терм-множество переменной , т.е. множество ее значений, причем каждое из таких значений (терм) есть название нечеткой переменной , областью определения которой является множество Х; G – синтаксическая процедура, порождающая на множестве T значения переменной ; М – семантическая процедура, которая отображает каждое новое значение нечеткой переменной в нечеткое подмножество М( ) множества Х.
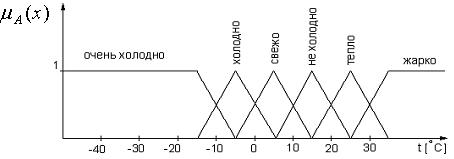
Рассмотрим пример. Пусть определяется температура окружающего воздуха с помощью понятий-значений: “очень холодно”, “холодно”, “свежо”, “не холодно”, “тепло”, “жарко”. Каждому понятию-значению соответствует определенная температура (рисунок 4.19). При этом минимальная и максимальная температуры соответственно равны – 40оС и +40оС. Тогда формально лингвистическая переменная “температура” представляется набором
< ТЕМПЕРАТУРА, {ОЧЕНЬ ХОЛОДНО, ХОЛОДНО, СВЕЖО, НЕ ХОЛОДНО, ТЕПЛО, ЖАРКО}, [-40,+40], G,M >,
где G – процедура перебора элементов терм-множества T; М – процедура, которая ставит в соответствие нечетким переменным (“жарко”, “тепло” и т.д.) температуру окружающего воздуха. Иными словами, процедура М определяет взаимосвязь нечетких переменных с соответствующими функциями принадлежности.
Рисунок 4.19 – Лингвистическая переменная “температура”
178 |
Глава 4 |
|
|
В зависимости от характера множества Х лингвистические переменные подразделяются на числовые и нечисловые. Числовой называется такая лингвистическая переменная, для которой базовая переменная определенна на числовом множестве. В рассмотренном выше примере лингвистическая переменная “ТЕМПЕРАТУРА” является числовой, а ее значения (нечеткие переменные) – нечеткими числами. Каждой нечеткой переменной на рисунке 4.19 условно соответствует треугольная или трапецеидальная функция принадлежности, которая определяет степень принадлежности той или иной температуры окружающего воздуха к соответствующему нечеткому понятию. Так, руководствуясь рисунком, нечеткую переменную “не холодно” можно определить с помощью следующего нечеткого множества
“не холодно”={(5|0),(15|1,0),(25|0)}.
В общем случае построение функции принадлежности осуществляют на основе экспертных оценок. Соответствующие процедуры построения функций принадлежности описаны в [31,36].
Нечеткие и лингвистические переменные позволят формулировать нечеткие утверждения. Например, “Сегодня не холодно” или “Если тепло и влажно, то овощи растут быстро” и т.п. Подобные утверждения являются объектом исследований нечеткой логики. Важно отметить, что в отличие от формальной логики, которая использует таблицы истинности, нечеткая логика опирается на операции, выполняемые над нечеткими множествами. Поэтому рассмотрим основные операции нечетких множеств.
Будем рассматривать нечеткие подмножества А и В множества Х. Не-
четкие |
множества А и В |
равны (обозначается |
А=В), если |
х Х |
|||
А(х) В(х). Множество |
В содержится в |
множестве |
А, |
если |
|||
х Х |
В (х) А (х). Множества А и В дополняют друг друга, |
если |
|||||
х Х |
В(х) 1 А(х). Множество с функцией принадлежности |
1 А(х) |
|||||
есть дополнение к множеству А (обозначается |
|
). |
|
|
|
||
А |
|
А В) – |
|||||
Пересечение двух нечетких множеств А и В (обозначается |
|||||||
это нечеткое множество, функция принадлежности которого определяется выражением
А В (х) min{ A(x), B (x)}, x X .
Объединением нечетких множеств А и В (обозначается А В) есть нечеткое множество с функцией принадлежности
А В max{ A (x), B (x)}, x X .

Основные модели вывода |
179 |
|
|
Операции пересечения и объединения нечетких множеств ассоциативны и дистрибутивны. В теории нечетких множеств часто используют обозначения А В (х) А (х) В (х) и А В (х) А(х) В (х). Здесь исоответствуют min и max.
Алгебраическое произведение нечетких множеств А и В (обозначается АВ) есть нечеткое множество, для которого
АВ (х) А(х) В (x), х Х .
Алгебраическая сумма нечетких множеств А и В (обозначается А ˆ В) есть нечеткое множество с функцией принадлежности
АˆВ(х) А(х) В(х) А(х) В(х).
Дизъюнктивная сумма нечетких множеств А и В определяется через операции объединения и пересечения
А В (А В) (А В) (А\ B) (B \ A),
где выражения А\ B А В и B \ A В А представляют соответствующие разности множеств А и В. В общем случае А\ B B \ A.
Важным понятием теории нечетких множеств является нечеткое отношение. Нечетким бинарным отношением Р : Х1 Х2 называется подмножество декартового произведения двух множеств Х1 и Х2
P {(x1,x2)| P(x1,x2)}, x1 X1, x2 X2 ,
где P (x1,x2 ) – функция принадлежности пары элементов (х1, х2) к Р.
В общем случае n-арное нечеткое отношение Р определяется на прямом произведении множеств X1 X2 Xn с помощью формулы
Р {(x1,x2 , ,xn )| ( P (x1,x2 , ,xn )},
где x1,x2,…,xn – элементы множеств Х1,Х2,…,Хn. Сопоставляя определение нечеткого множества и нечеткого отношения, можно заметить, что нечеткое отношение – это нечеткое множество, базовая переменная которого есть вектор. В качестве примера приведем бинарное нечеткое отношение. Пусть множества Х и Y состоят из элементов X={1, 2}, Y={1,1 , 2,1 , 5}. То-
