Точно Не проект 2 / Не books / Источник_1

ГЛАВА 4

ОСНОВНЫЕ МОДЕЛИ ВЫВОДА

Под выводом понимают процесс получения заключений из предпосылок. Существуют различные модели вывода. В главе 3 было введено понятие дедуктивного вывода в логике исчисления предикатов, который базируется на применении определенных правил вывода к множеству исходных истинных утверждений, и только лишь обозначено возможное направление автоматизации этого процесса. В данной главе рассмотрим общие процедуры, позволяющие автоматизировать дедуктивный вывод в исчислении предикатов, и, прежде всего, процедуру резолюции. С этой целью введем понятие предложения для формул исчисления предикатов, затем рассмотрим понятие универсума Эрбрана и, наконец, опишем процедуру резолюции и ее применения при решении различных задач.

Хотя исчисление предикатов является весьма мощным инструментом, подходящим для описания самых различных предметных областей, однако оно не лишено недостатков. В частности, теория исчисления предикатов позволяет получать правильные заключения, опираясь на общезначимые утверждения и обоснованные правила вывода. Вместе с тем часто требуется осуществлять вывод в условиях, когда исходные данные не являются абсолютно достоверными и полными, а правила вывода носят эвристический характер и ненадежны. В этом случае применяют процедуры, обеспечивающие вывод заключений с определенной степенью уверенности (процедуры вывода на ненадежных знаниях), а также процедуры немонотонного вывода, допускающие получение в ходе вывода заключений, которые могут логически противоречить утверждениям, имеющимся в базе знаний.

Кроме дедуктивного вывода, в системах искусственного интеллекта широко используют индуктивные схемы вывода. Такие схемы вывода позволяют порождать обобщения имеющихся частных утверждений. Способность к обобщению является важной функцией естественного интеллекта и используется им для получения новых знаний. Поэтому индуктивные схемы вывода являются элементом обучающихся подсистем искусственного интеллекта. Так как при обучении из совокупности имеющихся фактов

формируются путем обобщения новые понятия и правила, то индуктивные схемы вывода находят широкое применение при автоматизации процесса приобретения знаний.

Рассмотрим указанные модели вывода подробнее.

4.1. Дедуктивный вывод в исчислении предикатов

4.1.1. Формулировка задачи дедуктивного вывода

Вернемся к представлению задач в виде теорем (см. §2.1.3). Пусть задача описывается на языке исчисления предикатов. Если обозначить через Ф0 множество исходных утверждений и через Fg целевое утверждение, то задача, представленная в виде доказательства теоремы, формально может быть записана в виде

Ф0 Fg .

Иными словами, необходимо доказать, что формула Fg логически следует из множества формул Ф0.

Формула Fg логически следует из Ф0 , если каждая интерпретация, удовлетворяющая Ф0 , удовлетворяет и Fg. Когда множество Ф0 представлено формулами F1,F2,…,Fn, то задачей дедуктивного вывода исчисления предикатов является выяснение общезначимости формулы

F1 F2 ... Fn Fg .

В ходе вывода часто используют метод доказательства от обратного, т.е. устанавливают не общезначимость приведенной выше формулы, а невыполнимость формулы

F1 F2 ... Fn Fg

или

F1 F2 ... Fn Fg .

Иными словами, доказывают, что объединение Ф0 Fg невыполнимо. Та-

кое доказательство может быть существенно проще прямого вывода. Процесс установления невыполнимости некоторого множества формул назы-

вают опровержением.

Были разработаны эффективные методы автоматизации дедуктивного вывода. История их создания берет свое начало от основополагающих

тем не менее, решение задачи может быть найдено. Оно основывается на понятии универсума Эрбрана. Универсум Эрбрана представляет такую область интерпретации H, что если не существует интерпретации множества предложений S в этой области, то ее не существует вообще. Универсум Эрбрана строится из константных термов и определяется следующим образом:

а) множество всех предметных констант, встречающихся в S, принадлежит H; если в S нет констант, то в H включается произвольная константа а;

б) множество всех функций, встречающихся в S и определенных на множестве термов из H, принадлежит H.

Проиллюстрируем построение универсума Эрбрана на примере.

Пусть

SP (x, f (x,a)) Q(x,a) R(x,b) .

Вмножество S входят предметные константы а и b, функциональная буква f. В этом случае область H представляет бесконечное счетное множе-

ство:

H a,b, f (a,a), f (a,b), f (b,a), f (b,b), f (a, f (a,a)), f (a, f (a,b)),... ,

которое формируют последовательно в виде уровней:

H0 a,b ,

H1 a,b, f(a,a), f(a,b), f(b,a), f(b,b) ,

H2 a,b, f(a,a),...,f(b,b), f(a, f(a,a)), f(a, f(a,b)),...,...

Здесь H0, H1, H2 и т.д. – уровни универсума Эрбрана и H H . Дизъюнкт, который не содержит переменных, называется фунда-

ментальным. Он получается заменой предметных переменных константными термами. Если термы являются элементами универсума Эрбрана, то фундаментальный дизъюнкт называют фундаментальным примером дизъюнкта. Множество всех фундаментальных атомов вида P(t1, t2,… tn,), где Р

– предикатные буквы, встречающиеся в S, а t1, t2,… tn – элементы универсума Эрбрана, называется эрбрановской базой для S. Например, эрбрановской базой для рассматриваемого выше примера является множество:

A P(a, f (a,a)),Q(a,a),R(a,b),P(b, f (b,a)),... .

Задание интерпретации множества S в области H заканчивают, когда с каждой атомарной формулой эрбрановской базы связано соответствующее значение истинности.

дизъюнктов. Правило резолюции позволяет получать резольвенты множества дизъюнктов S. Если в процессе вывода резольвент получаются два од- но-литеральных дизъюнкта, образующих контрарную пару, то резольвентой этих двух дизъюнктов будет пустой дизъюнкт, обозначаемый символом

NIL.

Объединение исходного множества дизъюнктов с множеством всех резольвент, которые могут быть образованы из дизъюнктов, входящих в S, будем обозначать R(S). Применяя принцип резолюции к R(S), получим R(R(S)) R2 (S). В общем случае Rn 1(S) R(Rn (S)). При этом R0(S)=S. Легко заметить, что если множество S невыполнимо, то Ri(S) при любых i≥1 также невыполнимо, и наоборот, если невыполнимо Ri(S), то невыполнимо и S. Это свойство называется полнотой принципа резолюций. Оно устанавливается следующей теоремой, доказанной Робинсоном: если S – произвольное конечное множество дизъюнктов, то S невыполнимо тогда и только тогда, когда Ri(S) содержит пустой дизъюнкт. Данная теорема позволяет построить процедуру опровержения, которая для исходного множества S последовательно строит множества R1(S), R2(S),…Ri(S) и проверяет, содержит ли множество Ri(S) пустой дизъюнкт.

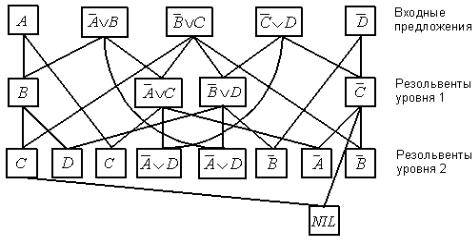
Вывод с помощью резолюции наглядно можно проиллюстрировать с помощью графа опровержения. Вершинами графа являются исходные дизъюнкты и резольвенты, получаемые в процессе вывода. Дизъюнкты исходного множества S представляют вершины графа, располагаемые в его верхней части. Если два дизъюнкта, находящиеся в каких-либо вершинах графа, образуют резольвенту (разрешаются), то вершина, соответствующая резольвенте, изображается ниже данных дизъюнктов и соединяется с ними ребрами.

В качестве примера на рисунке 4.1 построен граф опровержения множества исходных дизъюнктов:

S A, A B, B C, C D, D .

В логике высказываний нахождение контрарных пар не вызывает трудностей. Сложнее обстоит дело в логике предикатов. Например, если имеются дизъюнкты P(x, f (x)), P(a, y) Q(z), Q(b), то резольвента может быть получена только после выполнения следующих подстановок: а вместо x, f(x) вместо y, b вместо z. Затем по правилу резолюции получается пустое предложение.

Подстановкой называется конечное множество

t1 / x1, t2 / x2, ,tn / xn ,

Рассмотрим алгоритм построения НОУ на примере множества литералов:

P(g(x), x, f (x)), P(y,a,x) .

Если два литерала имеют общую переменную, то необходимо ее заменить новой переменной в одном из них. Заменив переменную x на z во втором литерале, получим P(x,a,z). Далее, рассматриваем слева направо каждый из литералов и находим позиции, в которых обнаруживается не совпадение термов. В данном случае не совпадают термы g(x) и y. Эти термы образуют множество рассогласования {g(x),y}, где y – переменная. Поэтому выполняется подстановка 1 g(x)/ y , которая преобразует множество исходных литералов к виду {P(g(x)), x, f(x)), P(g(x)), a, z)}. Продолжая процесс сопоставления термов, обнаруживаем несовпадение x и a, которые формируют множество рассогласования {x,a}, соответствующее подстановке 2 ={a/x}. Применив 2 к множеству унифицируемых литералов, получим {P(g(a)),a,f(a)),P(g(a)),a,z)}. Наконец, обнаружив несовпадение литералов f(a) и z, выполняем подстановку3 ={f(a)/z}. Таким образом, НОУ представляет композицию подстановок

3 1 2 3 .

Алгоритм поиска НОУ для двух литералов L1 и L2, не содержащих общих переменных, можно представить в виде процедуры [86]:

Procedure Unify(L1,L2); Begin

α:=[ ]; {пустая подстановка}

Q1:=L1; Q2:=L2;

While True Do

Begin

Построить множество рассогласования D для цепочек символов, образующих Q1 и Q2;

If D=[ ] Then Возврат(α); t1=first(D); t2=last(D);

If var(t1) and non_contain(t1,t2) Then α1:={ t2/t1}

Else If var(t2) and non_contain(t2,t1) Then α1={ t1/t2}

Еlse Выход('Неудача'); Q1:=Q1α1;

Q2:=Q2α1;

α :=αα1 End

End.