
Точно Не проект 2 / Не books / Источник_1
.pdf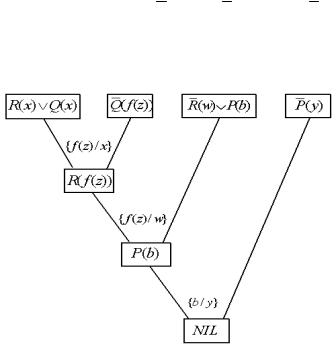
140 |
Глава 4 |
|
|
В этой процедуре полагается, что множество рассогласования D состоит из двух термов t1 и t2 , т.е. D={ t1,t2}. Тогда вызов функции first(D) соответствует выделению t1 – первого элемента множества, а вызов функции last(D) – выделению t2. Функция var(t) возвращает значение true, если аргумент t – переменная. Функция non_contain(x,y) – предикат, возвращающий значение true, если x не содержится в y. Если x входит в y, то унификация не выполнима. Например, нельзя унифицировать x и f(x).
Обобщая сказанное, отметим, что в логике предикатов нахождение резольвенты двух предложений (дизъюнктов) сводится к следующим действиям:
1)переменные в предложениях переименовываются так, чтобы они не совпадали;
2)находится подстановка (НОУ), при которой литерал одного предложения становится дополнительным к какому-либо литералу другого предложения;
3)дополнительные литералы вычеркиваются;
4)если получены одинаковые литералы, то все они, за исключением одного в каком-либо предложении, вычеркиваются;
5)дизъюнкция оставшихся литералов каждого из предложений и есть резольвента.
На рисунке 4.2 изображено дерево опровержения невыполнимого множества дизъюнктов S {R(x) Q(x), Q(f(z)), R(w) P(b), P(y)}, являющихся формулами исчисления предикатов. На дереве показаны дизъюнкты, получающиеся в результате соответствующих подстановок.
Рисунок 4.2 – Дерево опровержения
В процессе унификации могут получаться факторы дизъюнктов. Если несколько литералов дизъюнкта D имеют НОУ α, то Dα называют факто-

Основные модели вывода |
141 |
||||
|
|
|
|
|
|
ром. Например, пусть D Q(x) Q( f (y)) |
|
(x).Тогда НОУ |
α={f(y)/x} и |
||
P |
|||||
фактор D Q( f (y)) |
|
( f (y)).Факторы представляют собой |
подстановоч- |
||
P |
|||||
ные частные случаи, которые позволяют уменьшить дизъюнкты по длине. Принцип резолюции предполагает использование не только резольвент, но
ифакторов.
Вобщем, процесс опровержения не протекает столь эффективно, как изображено на рисунке 4.2. Во многих случаях множества R1(S), R2(S),…Ri(S) очень быстро разрастаются, так как непосредственное применение принципа резолюций соответствует “слепому” поиску.
Существует большое число модификаций принципа резолюций, направленных на нахождение эффективных стратегий поиска наиболее предпочтительных дизъюнктов для бинарной резолюции. Ниже рассмотрим кратко только некоторые из стратегий поиска, нашедших наиболее широкое применение.
4.1.5. Стратегии поиска
Для решения проблемы “комбинаторного взрыва”, возникающей при непосредственном применении принципа резолюций, необходимо осуществлять целенаправленный подбор предложений, участвующих в процессе унификации. Выбор должен выполняться так, чтобы пустое предложение достигалось как можно скорее. Конечно, на каждом этапе опровержения выбор зависит от текущей ситуации. Однако имеются общие стратегии поиска, которые, вне зависимости от контекста задачи, позволяют сократить число резолюций. Ниже рассмотрим следующие четыре стратегии: стратегию унитарности, стратегию опорного множества, стратегию исходных данных, линейную стратегию.
Стратегия унитарности. Согласно этой стратегии, предпочтение отдается тем бинарным резолюциям, где одно из предложений содержит единственный литерал. Такая стратегия гарантирует уменьшение длины результирующих предложений. Например, следствием одно-литерального предложения Р и предложения P Q R будет Q R, которое короче исходного предложения. Cтратегия унитарности упорядочивает выбор пар предложений, упрощая последующие этапы доказательства невыполнимости исходного множества дизъюнктов.
Стратегия опорного множества. Более эффективной может оказаться попытка исключить из рассмотрения сразу несколько предложений на основе понятия опорного множества. Невыполнимое множество предложений S можно разбить на два подмножества S1 и S2. Подмножество S1 состоит из аксиом, а S2 – из отрицаний тех предложений, которые необходимо
142 |
Глава 4 |
|
|
доказать. Очевидно, что подмножество S1 не содержит противоречий. Поэтому нахождение резольвент предложений из S1 не допускается. Опорным называют множество предложений, состоящее из дизъюнктов, входящих в S2, и резольвент тех пар предложений, из которых хотя бы одно принадлежит опорному множеству. Стратегия опорного множества допускает выполнение тех резолюций, в которых, по крайней мере, одно из предложений входит в опорное множество. Если опорное множество относительно небольшое, то это значительно сокращает пространство поиска. Достоинство стратегии опорного множества также состоит в том, что формируемое дерево опровержения легко интерпретируется человеком, так как оно управляется целью.
Если множество исходных предложений невыполнимо, то рассмотренная стратегия приводит к пустому предложению, т.е. она является полной. Стратегия опорного множества является специальным случаем более общей семантической резолюции [21].
Линейная резолюция. Сначала находится следствие двух предложений исходного множества S. На следующих этапах в резолюции участвует резольвента Сi, полученная на предыдущем шаге (называемая центральным дизъюнктом), и дизъюнкт B (называемый боковым), являющийся либо одним из дизъюнктов исходного множества S, либо центральным дизъюнктом Сj, который предшествует в выводе дизъюнкту Сi , т.е. j < i . Линейная стратегия является полной и одной из наиболее эффективных в реализации.
Стратегия входных данных. Такая стратегия соответствует линейной резолюции с одним ограничением: в качестве боковых дизъюнктов выбираются только дизъюнкты исходного множества S. Дерево опровержения, изображенное на рисунке 4.2, построено в соответствии со стратегией входных данных.
Входная резолюция является полной только, если предложения множества S являются дизъюнктами Хорна.
Рассмотренные стратегии поиска можно комбинировать. Например, стратегии унитарности и опорного множества. Кроме этого, можно упрощать множество исходных предложений S. Для этого исключаются тавтологии, предложения, содержащие уникальные литералы, подслучаи [26]. Например, если множество S содержит дизъюнкт P(x), то не имеет смысла включать в состав S дизъюнкты вида P(a) или P(a) Q(b), так как они представляют подслучаи P(x).
Разработано большое число стратегий поиска резольвент при доказательстве теорем. Основной способ решения проблемы “комбинаторного взрыва” заключается в использовании семантики и встраивании в правила вывода специфики конкретной предметной области [21].

Основные модели вывода |
143 |
|
|
4.1.6. Применения принципа резолюции
Применение принципа резолюции предполагает перевод исходной постановки задачи на язык исчисления предикатов. При этом рассматриваются два случая. В первом случае требуется выяснить, следует ли логически некоторая формула Fg из множества формул Φ0, во втором случае, который встречается гораздо чаще, ставится задача нахождения значения аргумента x, при котором данная формула Fg, содержащая x, следует из множества Φ0. Иными словами, во втором случае требуется сначала установить справедливость утверждения
0 xFg (x),
а затем найти значение переменной x, при котором указанное утверждение выполняется. Выясним, как извлечь из доказанной теоремы ответ на поставленный вопрос. Процесс формирования ответа рассмотрим на примерах задач информационного поиска, планирования перемещения робота, автоматического написания программ.
4.1.6.1 Информационный поиск. Пусть имеется база данных, содержащая сведения о химических соединениях. Например, факты, указывающие какие соединения считаются оксидами, и какой цвет имеет то или иное соединение. Допустим, что среди многих фактов, хранящихся в базе данных, имеется утверждение о том, что соединение MgO – оксид, и цвет данного оксида – белый. Эти факты можно представить на языке исчисления предикатов в виде двух одноместных предикатов: oxide(MgO) и white(MgO). Здесь в качестве имен предикатов выбраны слова английского языка oxide (оксид) и white (белый).
Пусть требуется установить, существует ли оксид белого цвета. Данный вопрос на языке исчисления предикатов запишется в виде
Fg (x) x(oxide(x) white(x)).
Формулу Fg(x), которую необходимо доказать, называют предположением. Найдем отрицание предположения
Fg (x) x(oxide(x) white(x))
и докажем, что множество S {oxide(MgO),white(MgO),oxide(x) white(x)}
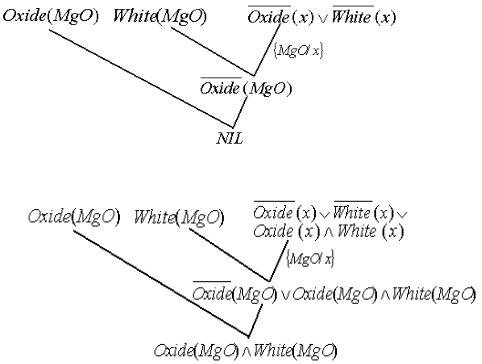
невыполнимо. Для этого построим дерево опровержения (рисунок 4.3). Затем необходимо извлечь то частное значение переменной, относя-
щееся к квантору существования, которое и служит ответом на поставлен-
144 |
Глава 4 |
|
|
ный вопрос. Для этого строят модифицированное дерево доказательства.
Процесс его построения состоит в следующем:
1)к отрицанию предположения дописывают через дизъюнкцию само предположение, т.е. вместо отрицания предположения записывают тавтологию;
2)находят резольвенты тех же предложений, которые участвовали в построении дерева опровержения.
Вкорне модифицированного дерева доказательства получается предложение, которое и используется в качестве развернутого ответа на поставленный вопрос. Модифицированное дерево доказательства изображено на рисунке 4.4.
Рисунок 4.3 – Дерево опровержения
Рисунок 4.4 – Модифицированное дерево доказательства
Интерпретируя предложение, находящееся в корне модифицированного дерева доказательства, заключаем, что существует оксид MgO, который имеет белый цвет.
Рассмотренный пример демонстрирует ответ на вопрос типа “да” или “нет”. Вопросы, относящиеся к типу “сколько”, также можно сформулировать в виде доказательства теорем. Пусть имеется правило [46]: “если в x есть m элементов типа y, а в y есть n элементов типа z, то в x есть m n элементов типа z”. Данное правило можно записать в виде формулы, используя предикат НР(а,b,с), который интерпретируется следующим образом: “а” содержит “с” элементов типа “b”. Тогда правило выражается в виде
Основные модели вывода |
145 |
|
|
x y{HP(x, y,m) HP(y,z,n) HP(x,z,times(m,n))},
где функция times(m,n) обозначает произведение m на n. Предположим, что под объектом х понимается человек. Системе известно, что человек имеет две руки, и на каждой руке – пять пальцев. Требуется выяснить, сколько пальцев на руках у человека? Безусловно, с точки зрения естественного интеллекта, это не вопрос. Однако отметим, что система должна формально вывести ответ на поставленный вопрос на основе известных ей фактов и общего правила.
Факты, известные системе, и вопрос можно записать в следующем
виде:
HP(man, hand, 2); HP(hand, fingers, 5);
k(HP(man, fingers,k)),
где man – человек, hand – рука, fingers – пальцы. Вопрос интерпретируется так: существует ли такое k , что справедливо HP(man, fingers, k).
Построим множество S. Для этого приведем правило к виду предложения
HP(x, y,m) HP(y,z,n) HP(x,z,times(m,n))
и найдем отрицание предположения
Fg (k) kHP(man, fingers ,k) .
Тогда
S {HP (man ,hand ,2),
HP (hand , fingers ,5),
HP (x, y,m) HP (y, z,n) HP (x, z,times (m,n)),
HP (man , fingers ,k)}.
Модифицированное дерево доказательства, построенное по принципу входной резолюции, изображено на рисунке 4.5. На первом шаге находится следствие предложения, представляющего правило, и отрицания целевого утверждения. На втором и третьем шагах используются факты HP(man,hand,2), HP(hand, fingers,5) . В корне дерева формируется ответ на поставленный вопрос HP(man, fingers, times(2,5)), т.е. количество пальцев на руках у человека можно вычислить с помощью вызова функции times(2,5).
146 |
Глава 4 |
|
|
HP(x, y,m) HP(y,z,n) HP(x,z,times(m,n))
HP(man, fingers,k) HP(man, fingers,k)
1 {man/ x, fingers/ z,times(m,n)/k}
2 {hand / y,2/ m}
HP(hand, fingers,n) HP(man, fingers,times(2,n))
HP(hand, fingers,5)
3 {5/n}
HP(man, fingers ,times (2,5))
Рисунок 4.5 – Модифицированное дерево доказательства
В рассмотренных выше примерах предположение содержало квантор существования. В тех случаях, когда предположение содержит квантор общности, возникают дополнительные трудности. Дело в том, что при отрицании квантора общности он переходит в квантор существования, который в процессе стандартизации предикатных формул исключается путем введения функций Сколема. Трудности состоят в интерпретации этих функций, если они появляются в ответном утверждении. В [30] рекомендуется такие функции заменять новыми переменными. При доказательстве в эти переменные не делают никаких подстановок.
4.1.6.2. Планирование перемещений робота. Данная задача форму-
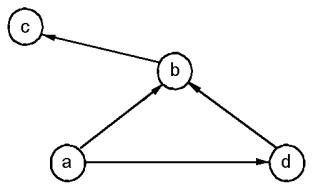
лируется как задача поиска пути на графе состояний (рисунок 4.6) [26,46]. В исходном состоянии задачи робот находится в позиции “а”. Необходимо найти последовательность операторов, обеспечивающих перемещение робота в позицию “с”, которая соответствует решенному состоянию задачи. Для решения задачи необходимо установить соответствие между описанием задачи в пространстве состояний и описанием ее на языке исчисления предикатов.
Операторам пространства состояний ставятся в соответствие функции языка исчисления предикатов. При этом преобразование состояния s1 в состояние s2 задается функцией s2=f(s1). Для участка графа состояний можно записать аксиому P(s1) Q(s2 ) или P(s1) Q( f (s1)), где P(s1) –
Основные модели вывода |
147 |
|
|
предикат, описывающий свойство начального состояния участка графа; Q(s2)- предикат, задающий свойство конечного состояния участка графа. Иными словами, если состояние s1 обладает свойством Р, то состояние s2=f(s1) обладает свойством Q.
Рисунок 4.6 – Граф состояний задачи перемещения робота
Введем функцию move(x,y,s), которая соответствует перемещению робота из точки х в точку у в состоянии s. Для описания состояния задачи будем использовать предикат AT(x, s), обозначающий, что для состояния задачи s робот находится в точке х. В этом случае можно записать следующие аксиомы:
AT(a,s0 ),
s1(AT(a,s1) AT(b,move(a,b,s1))),
s2 (AT(a,s2 ) AT(d,move(a,d,s2 ))),
s3(AT(b,s3) AT(c,move(b,c,s3))),
s4 (AT(d,s4 ) AT(b,move(d,b,s4 ))).
Целевое утверждение формулируется следующим образом: существует ли состояние задачи s, при котором робот будет находиться в точке “c”? На языке исчисление предикатов это можно записать в виде
sAT(c,s) .
Дерево опровержения для данной задачи изображено на рисунке 4.7. Результирующая функция, обеспечивающая переход робота из точки “а” в точку “с”, получается в результате серии подстановок в переменную s:
s= move(b, c, move(a, b, s0 )).
Выполнение действий в соответствии с этой функцией состоит в том, что робот сначала должен переместиться из точки “а” в точку “b”, а затем
148 |
Глава 4 |
|
|
из точки “b” в точку “с”. Рассмотренный подход использовался Грином в вопросно-ответной системе QA3 [46].
AT (b,s3 ) AT (c,move(b,c, s3 )) |
|
|
|
||||
AT (c,s) |
|||||||
|
|
{move (b,c, s3 ) / s} |
|
|
|
||
|
|
|
|
|
|||
|
(a,s ) AT (b,move (a,b,s )) |
|
|
(b,s3) |
|||
AT |
|
AT |
|||||
1 |
1 |
|
|
|
|
|
|
|
|
{move (a,b,s1 ) / s3} |
|
|
|
|
|
|
|
|
|
(a,s1) |
|||
|
|
AT (a,s0 ) |
AT |
||||
NIL
Рисунок 4.7 – Дерево опровержения для задачи поиска пути на графе
4.1.6.3. Автоматическое написание программ [30]. В этом примере продемонстрируем возможность автоматического написания простейшей программы с помощью принципа резолюции.
Рассмотрим задачу сортировки списка чисел х. Программа должна формировать упорядоченный по убыванию список чисел у. В этом случае можно сказать, что множество входных и выходных чисел удовлетворяет некоторому предикату (отношению) R(x, y). Если интерпретацию предикатной буквы R задать некоторым множеством аксиом и воспользоваться элементарными функциями, известными системе, то автоматическое написание программы сводится к тому, чтобы доказать, что предположениеx yR(x, y) логически следует из указанных аксиом. В ходе доказательства в переменную у будут сделаны необходимые подстановки элементарных функций, композиция которых и будет соответствовать решению задачи.
Для написания программы воспользуемся элементарными функция-
ми языка Лисп car, cdr, cons, merge. Вызовы функции car(x) и cdr(x) обес-
печивают выделение соответственно первого элемента списка х и оставшейся части списка (хвоста). Функция cons(x,y) добавляет элемент х в начало списка y 1). Функция merge(x,y) выполняет вставку элемента х в упорядоченный список у 2) . Отметим, что
1)Здесь мы используем правила записи функций языка исчисления предикатов. Синтаксис языка Лисп требует записи функций в несколько иной форме. Например, (car x).См. главу 5.
2)Функция merge языка Коммон Лисп имеет иной синтаксис вызова

Основные модели вывода |
149 |
|
|
cons(car(x),cdr(x))=x.
Сформулируем аксиомы, формализующие определение предиката R(x, y). Введем дополнительно предикат S(y), который означает, что “список y уже упорядочен”, и предикат I(x, y), означающий, что “списки х и у состоят из одних и тех же элементов”. Тогда будет верно следующее утверждение
x y{{R(x, y) [S(y) I(x, y)]} {[S(y) I(x, y)] R(x, y)}}.
Введем рекурсивные определения предикатов S(y) и I(x, y):
S(nil) (nil обозначает пустой список),
x y{S(y) S(merge(x, y))},
I(nil, nil),
x y u{I(x, y) I(cons(u,x),merge(u, y))}.
Преобразуем приведенные выше определения к множеству предложений, выполнив тождественные преобразования. Получим
Ф0 {R(x,y) S(y),R(x,y) I(x,y),S(y) I(x,y) R(x,y),
S(nil),S(y) S(merge(x,y)),I(nil,nil),I(x,y) I(cons(u,x),merge(u,y))}.
Запишем отрицание предположения:
Fg (x, y) x yR(x, y).
Исключив кванторы, получимR(a, y), где а – функция Сколема. До-
казательство невыполнимости множества формул { 0 R(a, y)} выполним по индукции: сначала для списков нулевой длины, а затем, предположив, что оно не выполняется для списка длины n 0, проверим доказательство для списка длины n+1.
Такая схема доказательства позволяет построить рекурсивное определение функции сортировки списков sort(x) и устраняет необходимость введения в рассмотрение предикатов с равенством.
Для списка х длины n=0 предположение можно записать в ви-
де yR(nil, y). Отрицание предложения запишется в виде R(nil, y). Модифицированное дерево доказательства для рассматриваемого случая изображено на рисунке 4.8 Ответное утверждение R(nil, nil) соответствует тривиальному результату: если список х пустой, то и результирующий список y тоже пустой
