4.4.2.4. Устойчивость точек покоя нелинейных систем по линейному приближению
Рассмотрим нелинейную систему дифференциальных уравнений
Здесь
Полагаем, что выполнены условия теоремы существования и единственности решения задачи Коши. Положим также, что при t ≥ t0 существует некоторое решение системы x = φ(t).
Точка x ≡ a называется точкой покоя (положением равновесия) системы x' = F(t,x), если F(t,a) = 0 при всех t ≥ t0. Точка покоя системы очевидно является решением системы.
Поскольку F(t,x) непрерывно дифференцируема и F(t,a) = 0, то при всех t ≥ t0, можно записать:
Обозначив
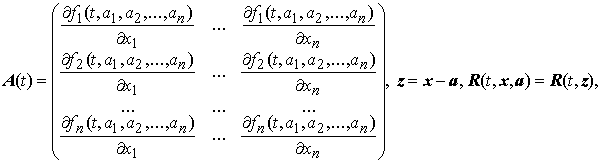
получим
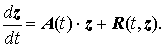
Системой первого (линейного) приближения для системы x' = F(t,x), называется линейная система
Очевидно, что тривиальное решение z ≡ 0 − точка покоя этой системы. Оказывается, что если точка покоя z ≡ 0 системы первого приближения асимптотически устойчива при t → ∞, то точка покоя x ≡ a системы x' = F(t, x) также асимптотически устойчива при t → ∞.
Точнее, справедливо следующее утверждение.
Теорема об устойчивости точки покоя по линейному приближению: Пусть x ≡ a − точка покоя системы x' = F(t, x). Пусть F(t, x) = A(t)·z + R(t, z), z = x − a. Вектор-функция R(t, z) непрерывно дифференцируема при t ≥ t0 , | z | < ρ и R(t, z) = ο(| z |) при | z | → 0, равномерно по t при t ≥ t0.
Если матрица A(t) = A постоянная матрица, действительные части всех собственных значений которой отрицательны, то точка покоя x ≡ a системы x' = F(t, x) асимптотически устойчива. При этом если | x(0) - a | достаточно мало, то при t ≥ t0 справедлива оценка | x(t) - a | ≤ C · exp(−α(t - t0)), α > 0, C> 0.
Пример №1
Исследуем на устойчивость нелинейную систему
Очевидно, что точка x ≡ 0 − точка покоя системы.
Запишем систему первого приближения:
Получили систему первого приближения, удовлетворяющую условиям теоремы об асимптотической устойчивости по первому приближению:
Точка покоя системы первого приближения x ≡ 0 асимптотически устойчива:
Следовательно, в соответствии с теоремой об устойчивости точки покоя по линейному приближению, точка покоя x ≡ 0 исследуемой системы, также асимптотически устойчива.
На рисунке изображены фазовая траектория исследуемой нелинейной системы (зелёный) и фазовая траектория системы первого приближения (синий). Обе траектории начинаются в точке (1, 0).
4.4.2.5. Неустойчивость по линейному приближению точек покоя нелинейных систем
Рассмотрим нелинейную систему дифференциальных уравнений
Здесь
Полагаем, что выполнены условия теоремы существования и единственности решения задачи Коши. Пусть x ≡ a − точка покоя системы.
Предположим, что системой первого (линейного) приближения для системы x' = F(t,x), называется линейная система
Здесь
Оказывается, что о неустойчивости точки покоя нелинейной системы можно судить по неустойчивости точки покоя её линейной системы первого приближения.
Точнее, справедливо следующее утверждение.
Теорема о неустойчивости точки покоя по линейному приближению: Пусть x ≡ a − точка покоя системы x' = F(t, x). Пусть F(t, x) = A(t)·z + R(t, z), z = x − a. Вектор-функция R(t, z) непрерывно дифференцируема при t ≥ t0 ,|z | < H и R(t,z) ≤ C | z |α.
Если A(t) = A постоянная матрица и если неустойчива точка покоя z ≡ 0 системы первого приближения z' = A·z, то неустойчива и точка покоя x ≡ a системы x' = F(t, x).
Пример №1
Исследуем на устойчивость нелинейную систему
Очевидно, что точка x ≡ 0 − точка покоя системы.
Запишем систему первого приближения:
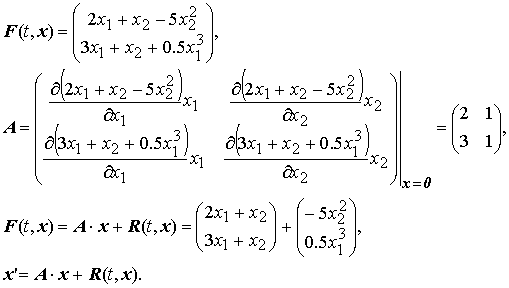
Получили систему первого приближения, удовлетворяющую условиям теоремы об асимптотической устойчивости по первому приближению:
Точка покоя системы первого приближения x ≡ 0 неустойчива:
Следовательно, в соответствии с теоремой о неустойчивости точки покоя по линейному приближению, точка покоя x ≡ 0 исследуемой системы также неустойчива.
На рисунке изображены фазовая траектория исследуемой нелинейной системы (зелёный) и фазовая траектория системы первого приближения (синий). Обе траектории начинаются в точке (0.01, 0).
