2.2. Основные свойства интеграла по мере области

1. Аддитивность относительно подынтегральной функции

(при этом каждый интеграл должен существовать).

Для доказательства достаточно учесть, что

2. Однородность

, С = const.

Это свойство следует из очевидного равенства

Объединяя свойства 1 и 2, можно сказать, что интеграл по мере области является линейным функционалом.

3. Если f (P) 1, то

.

Доказательство следует из определения интеграла по мере (формула (2.1)).

Конкретизируем это важное свойство:

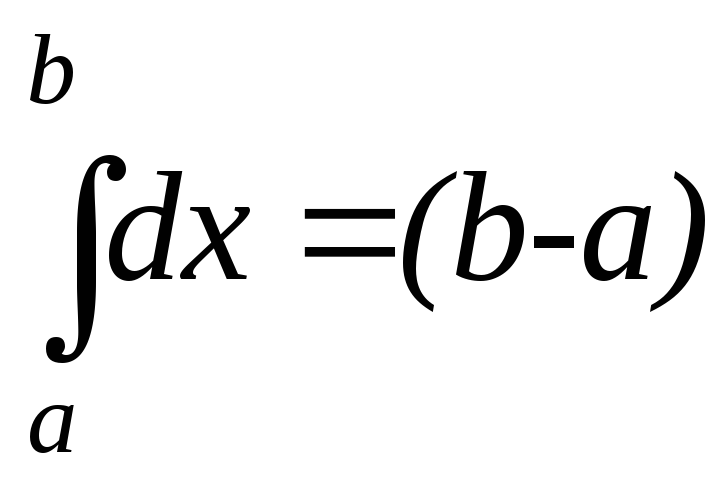• – длина отрезка ;

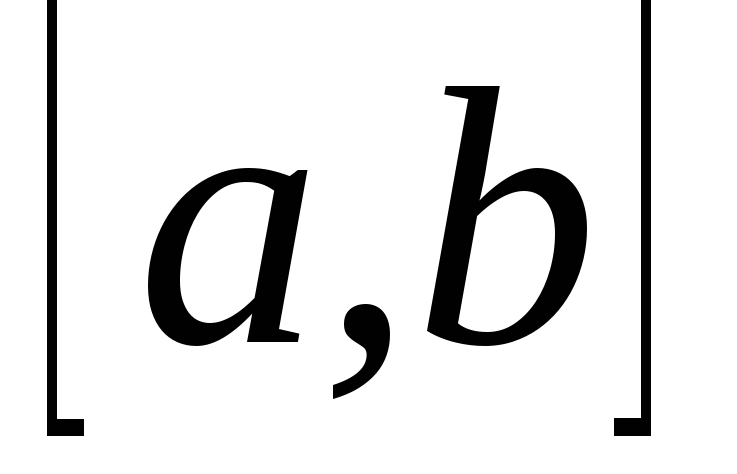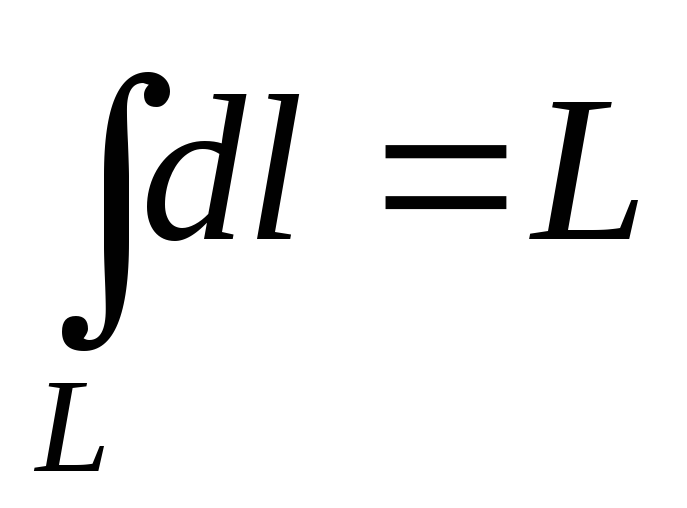• – длина линии L;

• – площадь области D;

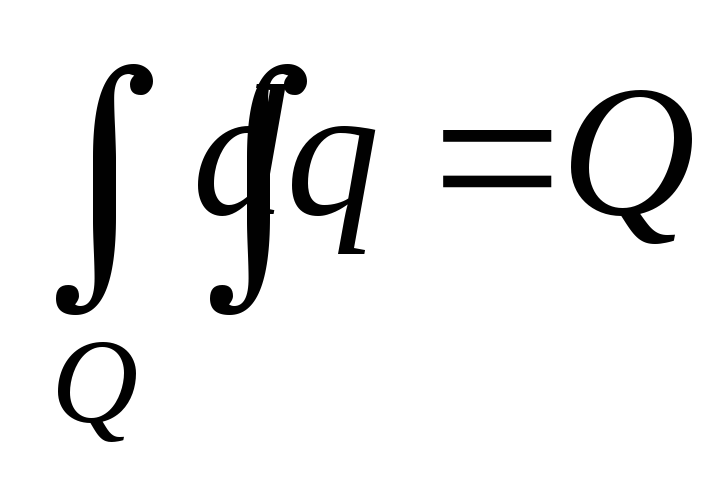• – площадь поверхности Q;

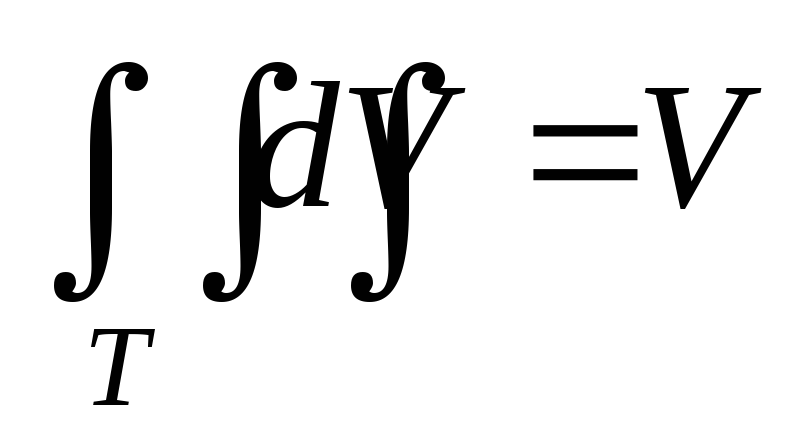• – объём тела Т.

4. Если , то

.

Например:

1) двойной интеграл по области G, которая является дугой кривой;

2) определенный интеграл, когда областью является точка, т. е. отрезок .

5. Аддитивность относительно области интегрирования

, если .

Доказательство

Рассмотрим область в пространстве R². Тогда

.

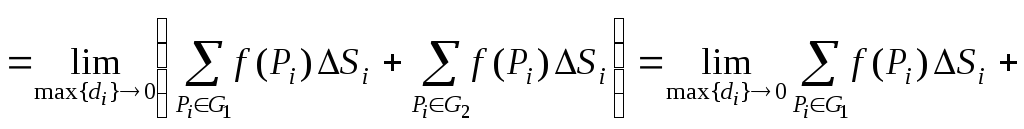
6. Теорема о знаке интеграла по мере.

Если .

Доказательство следует из определения интеграла по мере (формула (2.1)).

7. Если , то

.

Доказательство

Так как , то . Проинтегрируем обе части этого неравенства по области G:

.

Тогда

.

Из этого свойства следует, что неравенства можно почленно интегрировать.

8. Если , то

.

Доказательство следует из свойств 3 и 7.

Это свойство определяет двустороннюю оценку интеграла по мере.

Пример 1. Рассмотрим определенный интеграл.

Сравним площади фигур , , . Из рис. 2.5 очевидно, что

.

Вычислив площади прямоугольников, получим

.

9. Оценка модуля интеграла по мере области

.

Доказательство

По определению интеграла по мере имеем

.

Воспользуемся свойством модуля , тогда

.

Таким образом, получаем

.

10. Теорема о среднем значении функции в области с ненулевой мерой. Если функция f(P) непрерывна на замкнутой ограниченной фигуре G, то найдется такая точка , что

.

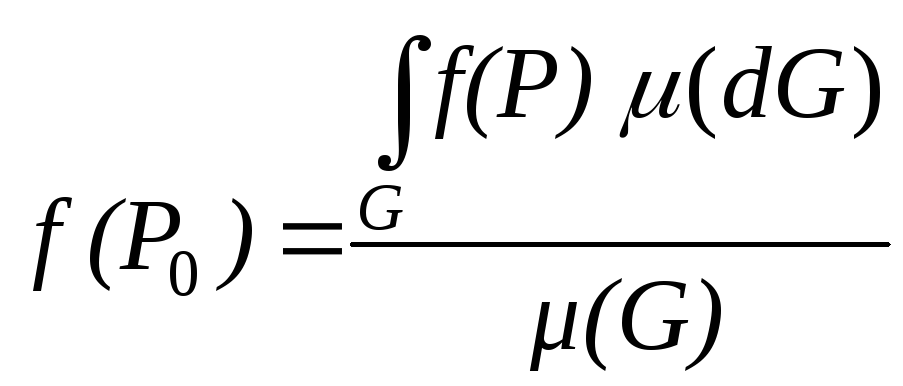Доказательство

Так как фигура G ограничена и функция f(P) непрерывна, то функция f(P) принимает на G свои наибольшее и наименьшее значения, т. е.

.

Проинтегрируем это неравенство

.

Воспользуемся свойством 8

.

Разделим неравенство на :

,

т. е. величина 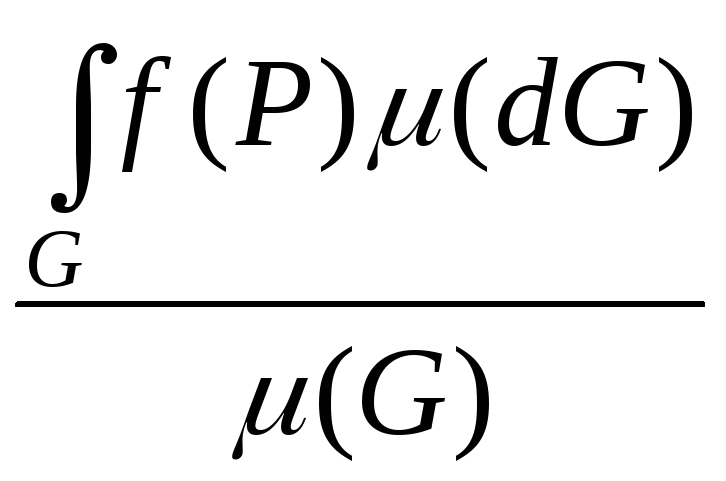заключена между и . Функция f(P) непрерывна и принимает значения между и . Значит, она должна принять и это значение в некоторой точке P₀. Таким образом,

.

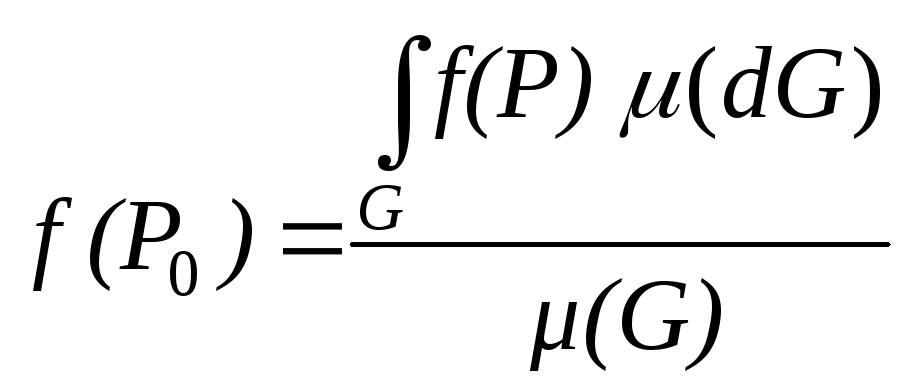Пример 2. Рассмотрим определенный интеграл.

На отрезке найдется точка такая, что площадь криволинейной трапеции аАВb будет равна площади прямоугольника аА₁В₁b (рис. 2.6):

.

Отсюда

.

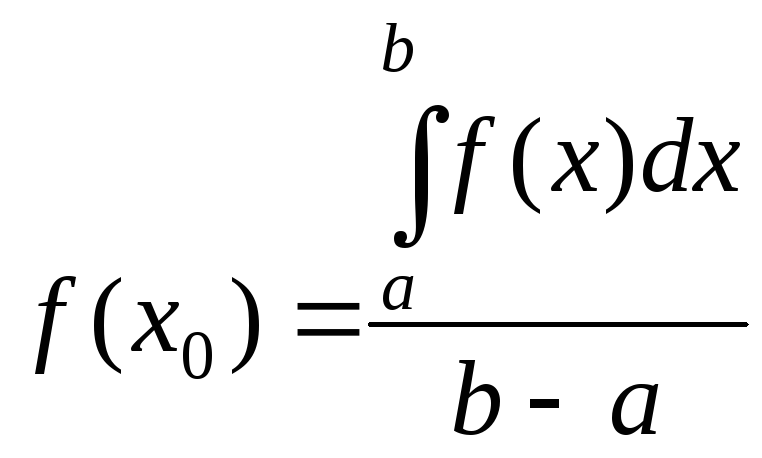2.3. Вычисление определенного интеграла

2.3.1. Формула Ньютона − Лейбница

Пусть . Как было показано ранее, определенным интегралом от функции f(x) по отрезку называется

, (2.8)

причем а называется нижним пределом интегрирования, b – верхним пределом интегрирования.

Если то величину определенного интеграла естественно принять за площадь криволинейной трапеции (рис. 2.7).

Формула, найденная Ньютоном и Лейбницем (независимо друг от друга), устанавливает связь между определённым и неопределённым интегралами. Она позволяет эффективно вычислять определенные интегралы и является основной формулой интегрального исчисления.

Разобьем отрезок на n частей (не обязательно равных по длине). Абсциссы границ полученных частей обозначим через :

.

Очевидно, справедливо равенство

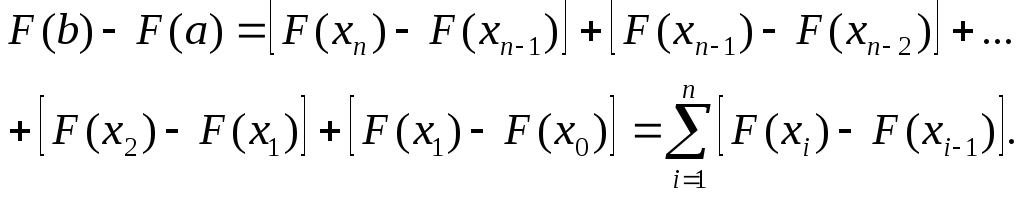(2.9)

Пусть Тогда по теореме Лагранжа

и формуле (2.9) можно придать вид

(2.10)

Формула (2.10) показывает, что при соответствующем выборе точек величина интегральной суммы при любом n постоянна и равна Поэтому при получим формулу

,

которую называют формулой Ньютона − Лейбница.

Определённый интеграл равен приращению первообразной от подынтегральной функции на отрезке интегрирования.

Для обозначения приращения функции на отрезке часто используют знак двойной подстановки

Формулу Ньютона − Лейбница можно вывести и другим способом.

Рассмотрим определённый интеграл

.

Для его существования необходимо, чтобы функция . Очевидно, что интеграл зависит от пределов интегрирования а и b.

Если закрепить а, а верхнюю границу сделать переменной, то интеграл

будет представлять некоторую функцию от х. Вычислим производную этой функции по переменной х. Для этого найдем

.

Тогда

.

Применим теорему о среднем

.

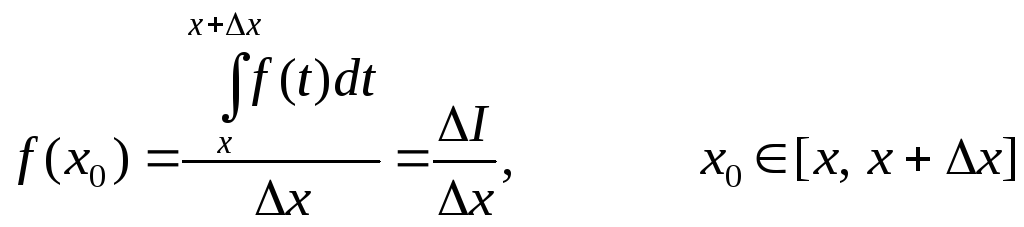Перейдем к пределу при

,

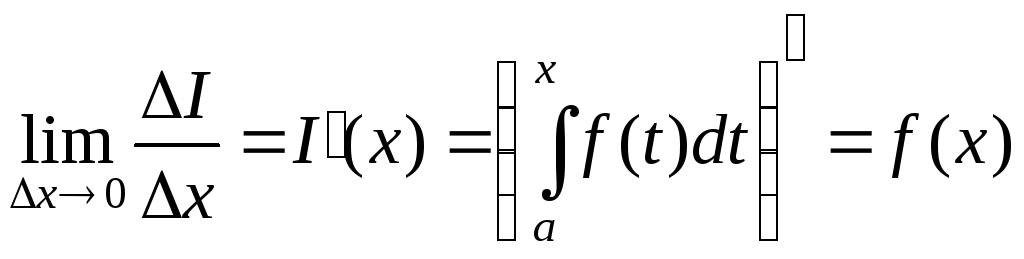так как при .

Итак, мы доказали теорему Барроу.

Теорема. Производная интеграла от непрерывной функции по переменному верхнему пределу равна подынтегральной функции, вычисленной на верхнем пределе.

Эта теорема является одной из основных теорем математического анализа и вскрывает глубокую связь между операциями определенного интегрирования и дифференцирования.

Следствие. Любая функция f(x), непрерывная на , имеет первообразную, выражаемую формулой

.

Исходя из геометрического смысла определённого интеграла как площади криволинейной трапеции, заметим, что соотношение

выражает переменную площадь криволинейной трапеции с основанием .

Теорема Барроу позволяет установить простой метод вычисления определённого интеграла.

Мы установили, что является первообразной для f(x). Первообразная имеет вид

.

Пусть х = а, тогда

.

Тогда . Подставим значение С в определение первообразной

.

Пусть теперь х = b, тогда

.

Получили формулу Ньютона – Лейбница, которая устанавливает связь между определённым и неопределённым интегралами от непрерывной функции f(x).

Пример 1. Вычислить .

Решение

.

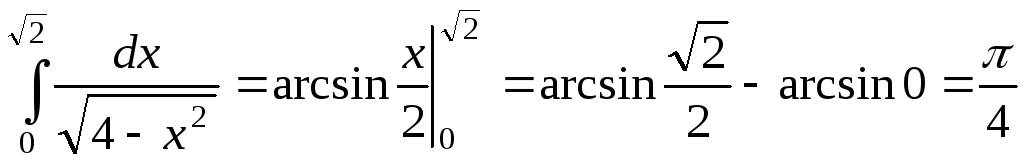Пример 2. Вычислить .

Решение

.

Пример 3. Вычислить .

Решение

.

Пример 4. Вычислить .

Решение

Под знаком интеграла стоит правильная рациональная дробь. Разложим подынтегральную функцию на сумму простейших дробей

.

Освободимся от знаменателя

т. е. .

Сравним коэффициенты при одинаковых степенях :

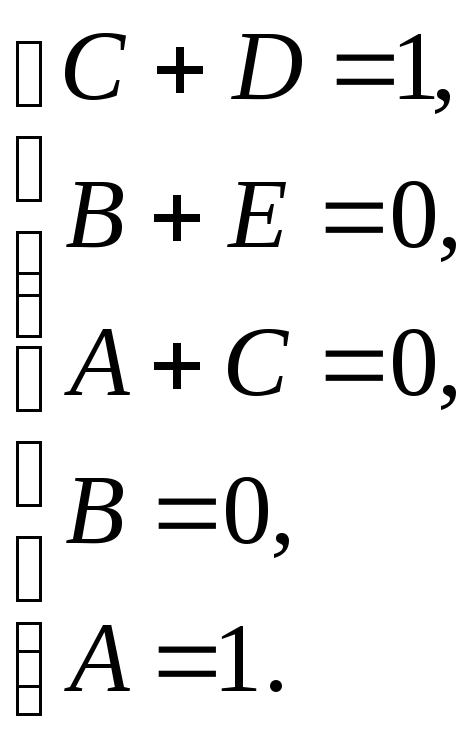
Находим, что .

Итак,

.

Пример 5. Вычислить .

Решение

.

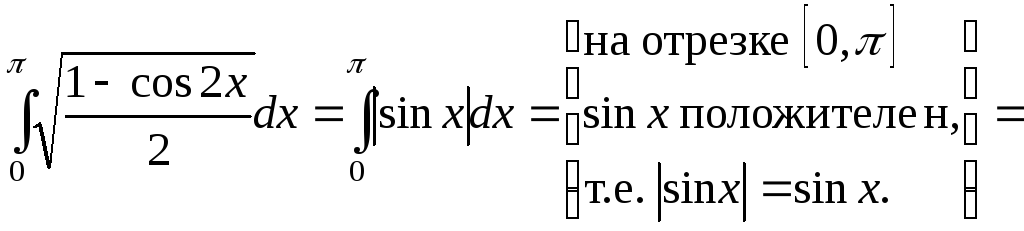
Пример 6. Вычислить .

Решение

.

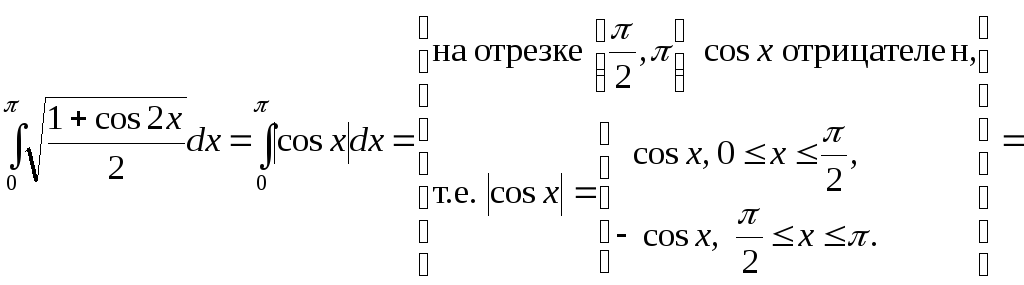
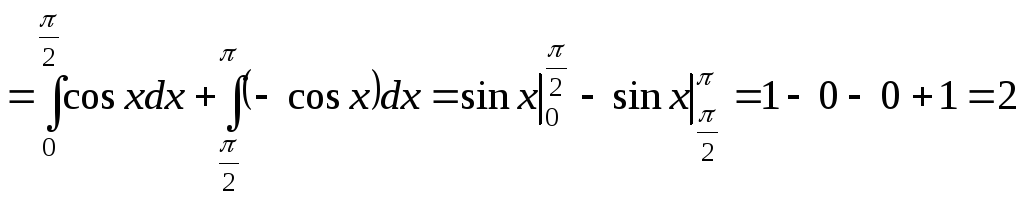Пример 7. Вычислить площадь криволинейной трапеции, ограниченной сверху кривой при

Решение

(кв. ед.)

Пример 8. Оценить интеграл .

Решение

Так как подынтегральная функция монотонно возрастает на отрезке , то наибольшее и наименьшее значение достигается на концах отрезка . Воспользовавшись свойством 8, получим

или .

Пример 9. Найти двустороннюю оценку интеграла .

Решение

Для рассматриваемого интеграла

; ; ; .

Для нахождения наибольшего и наименьшего значений функции на отрезке [a, b] исследуем функцию на экстремум:

,

,

или ,

,

.

Следовательно, на [a, b] функция f(x) экстремумов не имеет. Определяем значение функции на концах отрезка [a, b]:

,

.

Значит, . Воспользуемся свойством 8, получим