Задания для самостоятельного решения
Вычислить интегралы:
1.
(ответ:
).
2.
(ответ:
).
3.
(ответ:
).
4.
(ответ:
).
5.
(ответ:
).
6.
(ответ:
).
7.
(ответ:
).
8.
(ответ:
).
9.
(ответ:
).
1.8. Интегрирование иррациональных функций
1. Интегралы
вида
,
где R
– рациональная функция; m1,
n1,
m2,
n2,
… – целые числа
С
помощью подстановки
,
где s
– наименьшее общее кратное чисел n1,
n2,
…, указанный интеграл преобразуется в
интеграл от рациональной дроби.
Пример 1. Вычислить интеграл
.
Решение
.
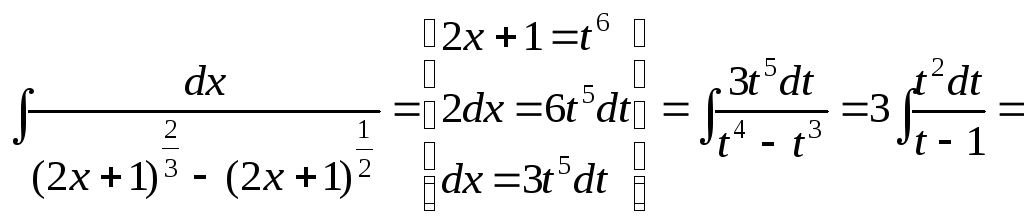
Пример 2. Вычислить интеграл
.
Решение
Так как наименьшее общее кратное чисел 2, 3, 6 равно 6, то
.
Интегрирование
некоторых функций, рационально зависящих
от
,
описано ранее в п. 1.6 «Интегрирование
функций, содержащих квадратный трехчлен».
2. Интегралы вида
Такой интеграл приводится к интегралу от рациональной функции новой переменной с помощью следующих подстановок Эйлера.
Первая
подстановка Эйлера.
Если
,
то полагаем
.
Перед корнем
возьмем для определенности знак плюс.
Тогда
,
откуда x определяется как рациональная функция от t:
(значит, dx тоже будет выражаться рационально через t), следовательно,
,
т. е.
оказывается рациональной функцией от
t.
Так
как
,
x
и dx
выражаются рационально через t,
то, следовательно, данный интеграл
преобразуется в интеграл от рациональной
функции от t.
Пример 1. Вычислить интеграл
.
Решение
Так
как
,
то
,
,
,
.
Подставляя полученные выражения в исходный интеграл, находим
.
Вторая
подстановка Эйлера.
Если
,
то полагаем
.
Перед корнем
возьмем для определенности знак плюс.
Тогда
,
откуда x определяется как рациональная функция от t:
.
Так
как
,
x
и dx
выражаются рационально через t,
то, следовательно, данный интеграл
преобразуется в интеграл от рациональной
функции от t.
Пример 2. Вычислить интеграл
.
Решение
Полагаем
,
тогда
,
,
,
,
.
Подставляя полученные выражения в исходный интеграл, находим
.
Третья
подстановка Эйлера.
Пусть
и
– действительные корни трехчлена
.
Полагаем
.
Так
как
,
то
,
,
.
Отсюда находим x как рациональную функцию от t:
.
Так
как
,
x
и dx
выражаются рационально через t,
то, следовательно, данный интеграл
преобразуется в интеграл от рациональной
функции от t.
Замечание
1. Третья
подстановка Эйлера применима не только
при
,
но и при
,
– лишь бы многочлен
имел два действительных корня.
Пример 3. Вычислить интеграл
.
Решение
Полагаем
,
тогда
,
,
,
,
,
.
Подставляя полученные выражения в исходный интеграл, находим
.
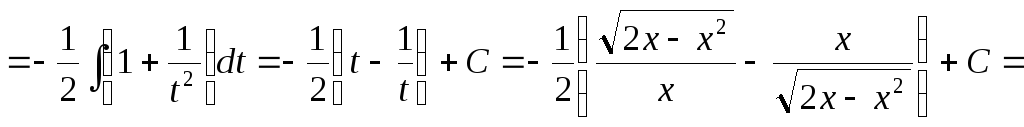
Замечание
2. Для
приведения исходного интеграла к
интегралу от рациональной функции
достаточно первой и третьей подстановок
Эйлера. Рассмотрим трехчлен
.
Если
,
то корни трехчлена действительны и,
следовательно, применима третья
подстановка Эйлера. Если
,
то в этом случае
и
трехчлен имеет знак, совпадающий со
знаком a.
Чтобы
был действительным, нужно, чтобы трехчлен
был положительным, а следовательно,
должно быть
.
В этом случае применима первая подстановка.